3.1.1 进位计数制
进位计数制是利用固定的数字符号和统一的规则来计数的方法。其中,最为人们熟知的便是十进制计数制。十进制计数制每位可以用0,1,2,3,…,9共计10个符号来表示,要想表示不一样的数值时,需要改变每个位置的符号即可。例如,1385.24代表的真实值是:
![]()
由此可见,对于任意一个十进制数
![]()
它的真实值可以表示为
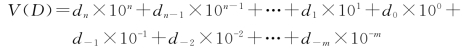
式中,d i(i=n,n-1,…,1,0,-1,-2,…,-m)可以取0、1、2、3、4、5、6、7、8、9这10个数字符号。这就是十进制数的表示方式。其中,“10”称为基数,它是指每个数位上可以取值的个数。10i 称为i位上的权。十进制数的计数规则是“逢十进一”。
推广开来,二进制数的计数规则是“逢二进一”,它每一位的数可以用0和1两个符号来表示。因此,它的基数为2,第i 位上的权是2i。例如,二进制数(110011.101)2 的真实值是:
![]()
由此可见,对于任意一个二进制数
![]()
它的真实值可以表示为
![]()
式中,bi(i=n,n-1,…,1,0,-1,-2,…,-m)只能用两个数字符号来代替,分别是0和1。
由于二进制数只有两个数字符号0和1,因而可以用具有两种稳定状态的元器件来表示,比如晶体管的饱和状态和截止状态,如果饱和状态用1来表示,则截止状态用0来表示。正是具有这种特性,计算机系统中广泛采用二进制数。
但是,当二进制数表示一个数位很长的数时,位数较长,书写、记忆不方便,因此,为了便于理解,计算机中又常使用八进制数和十六进制数来标记二进制数。八进制数和十六进制数只是为了使人们更好的理解、记忆二进制数,它们不能被计算机识别。
在八进制数中,有0、1、2、3、4、5、6、7共8个数字符号,计数基数为8,计数规则是“逢八进一”。例如,(37.56)8=3×81+7×80+5×8-1+6×8-2。
在十六进制数中,有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F共16个符号,计数基数为16,计数规则是“逢十六进一”。例如,(39DA)16=3×163+9×162+D×161+A×160。
由上可知,在计算机系统中常用的进位计数制有下面几种:
二进制,基数为2,基本符号为0和1。
八进制,基数为8,基本符号为0、1、2、3、4、5、6、7。
十进制,基数为10,基本符号为0、1、2、3、4、5、6、7、8、9。
十六进制,基数为16,基本符号为0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F(其中A、B、C、D、E、F的十进制的值为10、11、12、13、14、15)。
在书面表达时,后缀除了使用基数表示进位计数制外还可以用字母表示,二进制可以用B表示,八进制可以用O 表示,十进制可以用D 表示,十六进制可以用H 表示。其中,十六进制数也有用前缀0x来表示的,例如0xc000007b就是十六进制数c000007b。
使用计算机的用户为了理解和书写方便,大都采用十进制数进行表示,但是计算机只能识别二进制数。因此,用户理解的数据被输入计算机后计算机都要实现计数制的转换。下面介绍进位计数制之间的转换。
1.非十进制数转换为十进制数
将非十进制数转换为等值的十进制数,只需要将非十进制数的每一位按权展开相加即可。
【例3.1】 将下列二进制数转换为十进制数:
(10011.1)2=1×24+0×23+0×22+1×21+1×20+1×2-1=(19.5)10
【例3.2】 将下列八进制数转换为十进制数:
(247)8=2×82+4×81+7×80=(167)10(https://www.daowen.com)
2.十进制数转换为非十进制数
将十进制数转换为非十进制数时,十进制数的整数部分用连除取余法,转换为几进制数就除以几;十进制的小数部分用连乘取整法,转换为几进制数就乘以几。
(1)整数部分转换
【例3.3】 (748)10=(?)8
解:这是一道十进制数转换为八进制数的题目,其中十进制数只有整数位,因此转换时应用除8取余法进行。
因此,最终的结果为(748)10=(1354)8。

【例3.4】 (748)10=(?)16
解:这是一道十进制数转换为十六进制数的题目,其中十进制数只有整数位,因此转换时应用除16取余法进行。

因此,最终的结果为(748)10=(2EC)16。
(2)小数部分转换
【例3.5】 (0.6875)10=(?)2
解:这是一道十进制数转换为二进制数的题目,其中十进制数只有小数位,因此转换时应用乘2取整法进行。

因此,最终的结果为(0.6875)10=(0.1011)2。
【例3.6】 (0.45)10=(?)8
解:这是一道十进制数转换为八进制数的题目,其中十进制数只有小数位,因此转换时应用乘8取整法进行。

因此,最终的结果为(0.45)10≈(0.346)8。
【例3.7】 (748.45)10=(?)8
解:综合上面例题的结果,得(748.45)10≈(1354.346)8。
3.二进制、八进制、十六进制数的相互转换
二进制数转换为八进制或十六进制数时,将二进制数的整数部分由小数点向左,每3位或4位分成一组,不足3位或4位的,后面补零。小数部分由小数点向右,每3位或4位分为一组,不足3位或4位的,后面补零。然后,把每3位或4位二进制用等值的一位八进制数或十六进制数代替。
【例3.8】 (101 010.111110)2=(?)8
解:
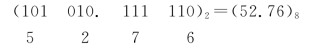
【例3.9】 (7AC)16=(?)2
解:
(7AC)16=(0111 1010 1100)2
由以上各例题可以看出,二进制数与八进制、十六进制之间有很简单的一一对应关系。如果一个很大的二进制数,记忆、理解不方便,那么就可以把它转换为八进制或者十六进制数来理解。虽然计算机系统只能识别二进制数,但是为了使用、书写更加方便,人们常常使用八进制或者十六进制数表示二进制数。
