2.3.1 组合逻辑电路的分析
组合逻辑电路分析,就是根据已知的逻辑电路图,分析确定其逻辑功能的过程。分析过程一般按下列步骤进行:
(1)写出逻辑函数表达式。根据已知的逻辑电路图,从输入到输出逐级写出逻辑电路的逻辑函数表达式。
(2)化简逻辑函数表达式。一般情况下,由逻辑电路图写出的逻辑表达式不是最简与—或表达式,因此需要对逻辑函数表达式进行化简或者变换,以便用最简与—或表达式来表示逻辑函数。
(3)列写真值表。根据逻辑表达式列出反映输入/输出逻辑变量相互关系的真值表。
(4)分析并用文字概括出电路的逻辑功能。根据逻辑真值表,分析并确定逻辑电路所实现的逻辑功能。
【例2.15】 已知逻辑电路如图2.18所示,分析该电路的逻辑功能。
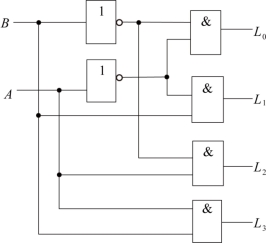
图2.18 逻辑电路图
解:由逻辑电路图可知,此逻辑电路由反相器和与门两种门电路共同组成。电路有2个输入变量A、B,4个输出函数分别为L 0、L 1、L 2、L 3。
①根据逻辑电路图写出逻辑函数表达式:
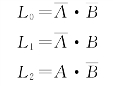
L 3=A·B
②由逻辑函数式列出真值表,如表2.13所示:
表2.13 真值表

③由表2.13可知:
当AB=00时,L 0=1,其余的输出端均为0;
当AB=01时,L 1=1,其余的输出端均为0;
当AB=10时,L 2=1,其余的输出端均为0;
当AB=11时,L 3=1,其余的输出端均为0。
④由此可以得知,此电路对应每组输入信号只有一个输出端为1,因此,根据输出状态即可以知道输入的代码值,而具有这样特征的逻辑电路被称为译码器,故此逻辑电路具有译码功能,而且输出端是高电平有效。
⑤结论电路的逻辑功能为译码功能。
【例2.16】 组合电路电路图如图2.19所示,试分析该电路的逻辑功能。
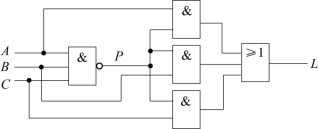
图2.19 逻辑电路图
解:
①由逻辑电路图写出逻辑表达式。为了便于书写表达式,借助中间变量P,于是
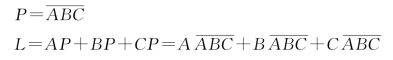 (https://www.daowen.com)
(https://www.daowen.com)
②化简与变换。
变换的目的是使表达式有利于列真值表,一般应变换成与—或式最小项表达式:
![]()
③由表达式列出真值表,如表2.14所示。
表2.14 真值表
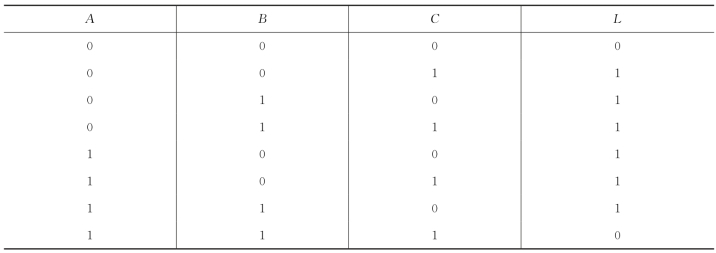
④分析逻辑功能。
由表2.14可知,当A、B、C 三个变量不一致时,电路输出为1,所以这个电路称为“不一致电路”。
对于比较简单的组合逻辑电路,也可通过其波形图进行分析。即根据输入信号的波形,逐级画出输出信号的波形,根据输入与输出波形的关系确定其电路的逻辑功能。
【例2.17】 已知逻辑函数的逻辑关系如图2.20波形图所示,其中A、B、C、D 为输入变量,L 为输出函数。试分析并列出函数真值表、逻辑函数表达式,并画出逻辑电路图。
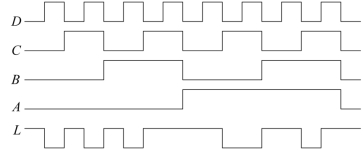
图2.20 信号波形图
解:分析图2.20波形图,可依据输入变量的不同波形组合,找出输入量与输出量的对应关系。
写出其真值表,如表2.15所示。
表2.15 真值表
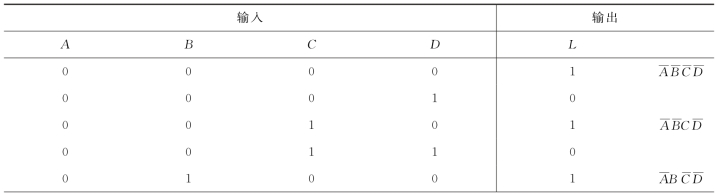
续表
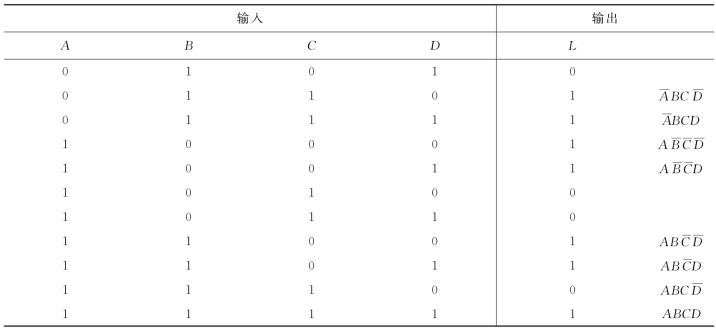
同一组变量取值组合使输出函数值为1,则各个变量之间的关系是与的关系且每个变量聚合为0时用反变量表示,取值为1时用原变量表示。例如,变量聚合ABCD=0000时,输出函数值为1,则表明各个变量以反变量的形式相与,即AB C D,其余组合类推。多种变量取值组合使输出函数值为1,则它们之间的关系是或的关系。按照这一原则,结合表2.15中的分析可写出如下输出函数的表达式:
L=![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +ABCD 在求输出函数表达式时,也可以由真值表的输入/输出对应关系直接画出所对应的卡诺图(图2.21),并在卡诺图上进行化简,进而画出输出函数表达式。
+ABCD 在求输出函数表达式时,也可以由真值表的输入/输出对应关系直接画出所对应的卡诺图(图2.21),并在卡诺图上进行化简,进而画出输出函数表达式。
在卡诺图上进行化简,得到简化的逻辑函数表达式如下:
![]()
上面的逻辑电路表达式可以通过反相器、与门、或门实现。其逻辑电路图如图2.22所示。
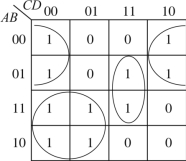
图2.21 卡诺图
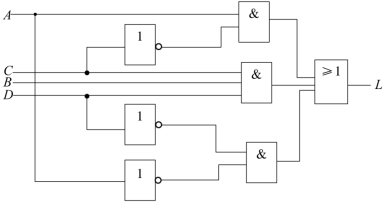
图2.22 逻辑电路图
