2．4．3 同步时序逻辑电路的设计
在设计时序逻辑电路时，要求设计者根据给出的具体逻辑问题，求出实现这一逻辑功能的逻辑电路，所得到的设计力求简单。在这一小节里首先讨论简单时序电路的设计。这里所说的简单时序电路，是指用一组状态方程、驱动方程和输出方程就能完全描述其逻辑功能的时序电路。
当选用小规模集成电路做设计时，最简的电路所用的触发器和门电路的数目最少，而且触发器和门电路的输入端数目也最少。而当使用中、大规模集成电路时，最简的电路是使用的集成电路数目最少，种类最少，而且互相间的连线也最少。
同步时序逻辑电路的设计步骤：
（1）根据设计要求设定状态，导出对应状态图或状态表。这种直接由设计要求导出的状态图（表）称为原始图（表）。
（2）状态化简，原始状态图通常不是最简的，往往可以消去一些多余状态，称这一过程为状态化简。化简后的状态图称为简化状态图。
（3）状态分配，又称状态编码，即把一组适当的二进制代码分配给简化状态图中各个状态。由于二进制的每一位都将用一个触发器的状态来表示，因此，状态分配就是用触发器的状态编码表示状态图中的状态，得到编码状态表。在完成状态的同时也就确定了触发器的个数。触发器的个数n与电路状态的个数M 满足的关系：
2n≥M＞2n-1
（4）选择触发器的类型。触发器的类型选得合适，可以简化电路结构。
（5）根据编码状态表以及所采用的触发器的逻辑功能，导出待设计电路的输出方程和驱动方程。
（6）根据输出方程和驱动方程画出逻辑电路图。
（7）检查电路能否自启动。当电路的有效状态不是2n时，应检查电路能否自启动。如果电路不能自启动，则需重新设计电路或采取适当的措施解决问题。
【例2．24】 时序电路如图2．50所示，试分析其逻辑功能。
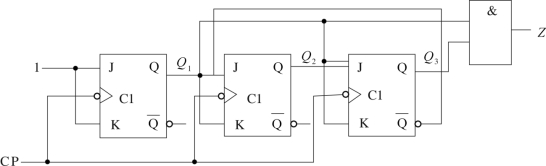
图2．50 时序电路图
解：①写出各逻辑方程式。
这是一个由JK 触发器组成的同步时序电路，每个触发器都是在CP下降沿作用下进行状态转换，可以省略时钟方程。
②驱动方程：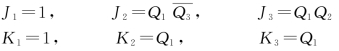
③输出方程：
Z＝Q 1Q 3
④将驱动方程代入JK 触发器特性方程中，求得状态方程：
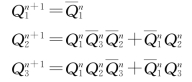
⑤列状态表并画状态图和时序图。
设电路初态
＝000，代入状态方程和输出方程，可求出
＝001，Z＝0。照此方法，求出所有
取值对应下的
和Z，列成状态表，如表2．28所示。
表2．28 状态表
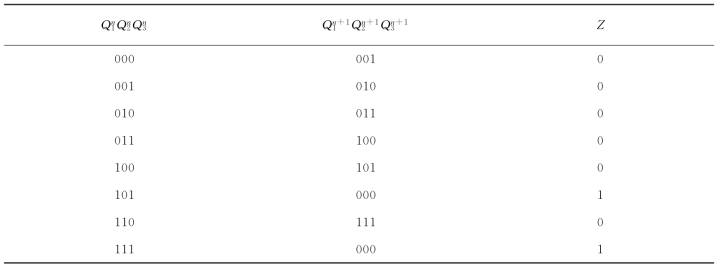
根据状态转换表可画出状态转换图，如图2．51所示。
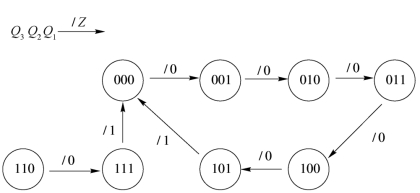
图2．51 状态转换图
由于此电路没有输入信号，所以状态图中斜线上方空着。另外，完整的状态转换图一定要画上图标J 3＝Q 1Q 2Q 3 和/Z。
根据状态表和状态图，可画出该电路的波形图，如图2．52所示。
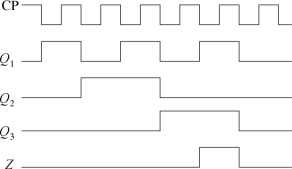
图2．52 波形图
⑥逻辑功能说明。
在CP脉冲的作用下，Q 1Q 2Q 3 的状态从000到101，以递增的形式每输入六个CP脉冲信号循环一次。可见，该电路对时钟脉冲信号有计数功能。所以，这个电路是一个同步六进制加计数器，Z 为进位位。000～101这六个状态为有效状态，有效状态构成的循环为有效循环。110和111状态为无效状态。无效状态在CP脉冲作用下能够进入有效循环，说明该电路能够自启动。若无效状态在CP作用下不能进入有效循环，则表明电路不能自启动。
另外，由此可以看出，Z 和Q 3的变化频率是CP输入脉冲频率的1/6，所以，又可将计数器称为分频器。
【例2．25】 设计一个同步五进制加法计数器。
解：设计步骤：
①根据设计要求，设定状态，画出状态转换图。五进制计数器有5个不同的状态，分别用S 0，S 1，…，S 4表示。在计数脉冲CP作用下，5个状态循环翻转，在状态为S 4 时，进位输出Y ＝1。状态转换图如图2．53所示。
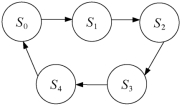
图2．53 状态转换图
②状态化简。五进制计数器应有5个状态，不需化简。
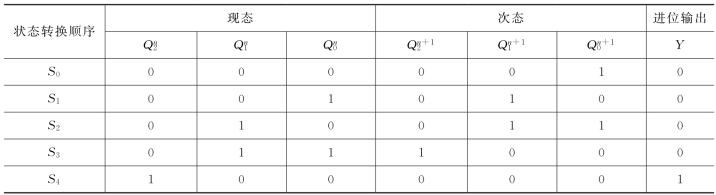
③状态分配，列状态转换编码表。由2n≥M＞2n-1可知，应采用3位二进制代码。该计数器可选用3位自然二进制加法计数编码，其状态转换表如表2．29所示。
表2．29 状态转换表
④选择触发器。本例选用功能比较灵活的JK 触发器。
⑤求各触发器的驱动议程和进位输出方程。
列出JK 触发器的驱动表，如表2．30所示。
表2．30 JK 触发器的驱动表
画出该计数器的次态卡诺图，如图2．54所示。
图2．54 卡诺图
3个无效状态101、110、111做无关项处理。根据次态卡诺图和JK 触发器驱动表可得各触发器的驱动卡诺图，如图2．55所示。
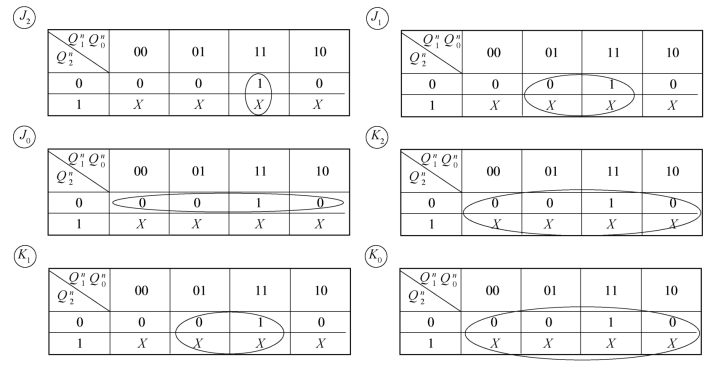
图2．55 卡诺图
通过驱动卡诺图写出驱动方程：以J 0、K 0 为例，对现态
＝000，其次态为
＝001，即Q 0由0变1，根据JK 触发器的驱动表，J 0＝1，K 0＝X，所以在J 0、K 0卡诺图000的位置分别填入1、X。依此类推，将5个有效状态对应的格填完。在3个无效状态对应的格中填入X，整个卡诺图就填完了。经画圈化简，得最简表达式J 0 ＝
，K 0＝1。同理，可得到其他触发器的驱动方程。
再画出输出卡诺图，如图2．56所示。
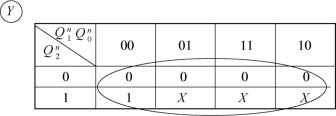
图2．56 卡诺图
可得电路的输出方程
将各驱动方程与输出方程归纳如下：
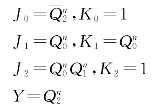
⑥画逻辑电路图。根据驱动方程和输出方程，画出五进制计数器的逻辑图，如图2．57所示。
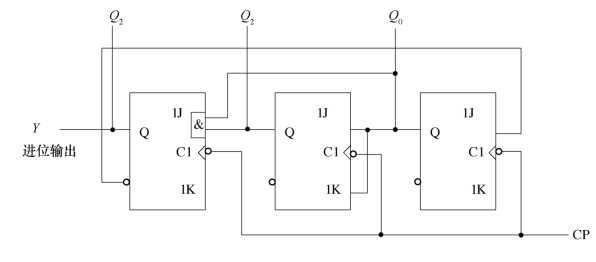
图2．57 逻辑电路图
⑦检查能否自启动。利用逻辑分析的方法画出电路完整的状态图，如图2．58所示，可见，如果电路进入无效状态101、110、111时，在CP 脉冲作用下，分别进入有效状态010、010、000，所以电路能够自启动。
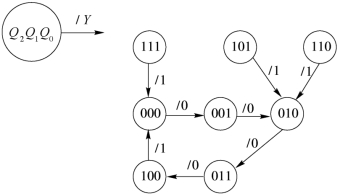
图2．58 状态转换图