3．7．6　浮点运算

3．7．6　浮点运算

1．浮点数加减运算

浮点数由于具有小数点，并且小数点的位置不固定，因此不能直接做加减运算。例如0．254×104＋0．571×103。对于这个浮点数的加法运算来说，两个浮点数的阶不同，因此并不能直接把尾数相加，而是先要把阶调整一致后才能相加。手动计算过程如下：

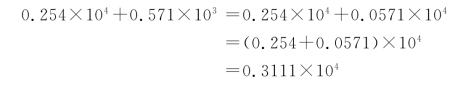
由这个例子我们可以得到一般方法。设两个浮点数a＝M a×2Ea 和b＝M b×2Eb，M 为尾数，E 为阶。则

a＋b＝(M a×2Ea-Eb＋Mb)×2Eb

a-b＝(M a×2Ea-Eb-Mb)×2Eb

计算机中计算浮点数的方式与其类似，要经过对阶、尾数运算、规格化、舍入等操作。

对阶，顾名思义就是指使两个浮点数的阶一致。对阶完成后才能做尾数运算。具体对阶方法为阶小的数的尾数右移，右移时符号位不变，数值位中的隐含的1同样要右移，前面空位补0。

对阶完成后就可以进行尾数运算了。在尾数运算时，隐藏位还原到尾数位，对阶时保留的附加位也要参加运算。

规格化是指把浮点数运算的结果进行移位操作。规格化分为右规和左规两种。右规是指尾数右移，阶数相应增加。最后右移的位要舍入。左规是指数值位左移，阶数相应减少。

舍入是指尾数右移时，将低位移出的位保留下来，参加运算，然后将运算结果舍入。

2．浮点数乘除运算

前面说到浮点数的加减运算需要进行对阶操作，浮点数的乘除运算不需要进行对阶操作，但是需进行规格化、舍入等操作。浮点数的乘除运算的一般方法为

设两个浮点数a＝M a×2Ea 和b＝Mb×2Eb E。乘除运算结果为

此外，在进行浮点数的加减乘除运算时要注意在计算机运算时有时不会满足四则运算的结合律等。例如，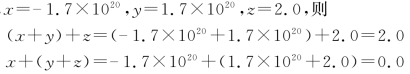

可以看到，在进行结合律时，运算出现了错误。这个错误出现的原因是对阶运算时2．0的尾数右移20位后被丢弃，相当于计算机把2．0当成了0．0。