石油库存
上个小节介绍了基于卫星图像形成的NDVI指数对玉米期货的影响,本小节我们再次转向能源期货,分析Orbital Insight(OI)基于卫星图像形成的石油库存对油价的影响。这个案例改编自Mukherjee et al.(2021)发表在金融期刊《金融经济学杂志》上的文章。
前面我们看到了很多官方公布的数据对金融市场的影响,比如非农就业人口数据对于利率和汇率等宏观资产以及农作物产量数据与农产品期货的影响,在石油这样的能源市场上也有这样的官方报告,这就是美国能源信息管理局(Energy Information Admininstration/EIA)每周发布的原油库存报告。这家政府机构要求石油市场的参与者每个周五上午7:00要填报EIA-083表,披露和石油库存有关的信息。这种信息披露是强制性的,如果未能及时准确地提交数据,那就面临来自官方的处罚。接受调查的公司总计占全美石油库存的90%。在汇总了反馈回来的数据之后,EIA通常会在下周三美国东部时间上午10:30,也就是五天之后发布石油形势报告(Petroleum Status Report)。[17]
近些年来,一些卫星智能公司开始实时估计位于全球各地的石油库存,比如Oribital Insight和Ursa Space等。虽然全球金融市场的投资者对这些数据很感兴趣,但是它们的准确性还存在着疑问。换句话说,我们希望了解基于卫星的石油库存估计是否充分有效,从而让金融市场可以在政府统计数据发布之前就融入其信息含义呢?当然这个问题并不局限于当前研究的石油库存,同样也适用于我们前面看到的基于NDVI形成的产量估计,以及在本章最后小节中看到的各种基于另类数据形成的对其他宏观经济活动的度量指标。
要回答这个问题的一个简单方法就是我们在上个小节NDVI分析中看到的事件研究方法,也就是讨论资产价格对于政府发布的宏观经济信息做出的反应。简单来说就是将公告前的政府数据不可用时段和公告后的数据可用时段进行对比,然后探讨在类似卫星图像这样的另类数据开始引入之后,资产价格对政府公告的反应是否会变小。这种想法的问题是,首先资产价格的反应程度变小可能是同期的其他因素导致的,比如政府可能会在公告之前提供其他相关的信息,更不用说我们在上一章中看到的联储的信息泄露案例。更重要的难题是内生性问题。也就是说,另类数据的应用本身是相应市场对特定资产信息的需求而出现的。比如说石油价格是全球重要的资产价格,那么除了卫星智能公司提供库存估计,市场的分析师也有动力提供更高质量的预测。这样资产价格的变动就可能是分析师预测带来的,而不是应用卫星数据带来的。而且卫星智能公司选择提供针对某个特定宏观变量的估计和预测也反映了这家公司的选择。显然内生性问题会干扰到对另类数据有用性的判断。为了解决这个问题,一个典型的方法就是让基于另类数据的估计值(或者预测值)的准确性能够外生地随机变化。比如像Fuchs-Schündeln/Hassan(2016)所设想的环境,能够随机地开放和关闭宏观经济估计背后的另类数据源,这样我们就可以对比数据源开放和关闭这两种情况下资产价格在政府公告日的反应差异。
为了实现上述的“理想环境”,作者提出了两个重要的洞见。首先,我们不需要在整个国家的范围内对另类数据源进行上述“开关”的随机化处理,而只需要衡量少数几个地点的经济活动,例如制造中心或者供应链中的枢纽,因为这些地区的经济指标对于宏观估计而言至关重要。因此,只要能够对这些特定地点另类数据的可用性做到随机化处理,就可以实现数据质量的外生差异了。举例来说,如果我们需要估计在大剧院中的观众人数,我们不需要统计每一位观众(类似人口普查)或者是对剧院的某片区域进行随机抽样,一种简单的办法就是统计在演出开始前几分钟通过入口进入剧场的人数。[18]就美国原油市场而言,图4.4描绘了美国的五个国防区域石油管理局(Petroleum Administration for Defense Districts/PADD),其中还显示了2016年底各个PADD区域的石油库存。[19]我们可以看到PADD2和PADD3区占总库存的80%以上。另外在这两个区域中有几个关键点是多条管道交汇的地方,显然它们是石油库存的枢纽。就原油的管网运输而言,这些交汇点可以灵活地引导原油流动,以应对市场供需的变化。这些地点中最重要的当然就是位于俄克拉荷马州的库欣:截至2016年底,其原油库存大约是美国的14%。而且库欣也是纽约商品交易所(NYMEX)西德州原油(WTI Light Sweet Crude Oil/WTI)期货合约的交割和价格结算地,而西德州原油期货是全球交易量最大的石油期货合约,本小节的案例将以这个商品资产为对象。经过观察之后,作者将注意力集中于十个特定地理位置,它们在图4.4中用圆圈表示。除了库欣之外,这些地点还包括路易斯安那离岸油港(Louisiana Offshore Oil Port/LOOP)、休斯顿、米德兰(Midland)、帕托卡(Patoka)以及墨西哥湾的几个重要地点。这十个地点的石油库存占据了全美的三分之一。[20]
图4.4 美国五大PADD区域以及主要石油库存地点
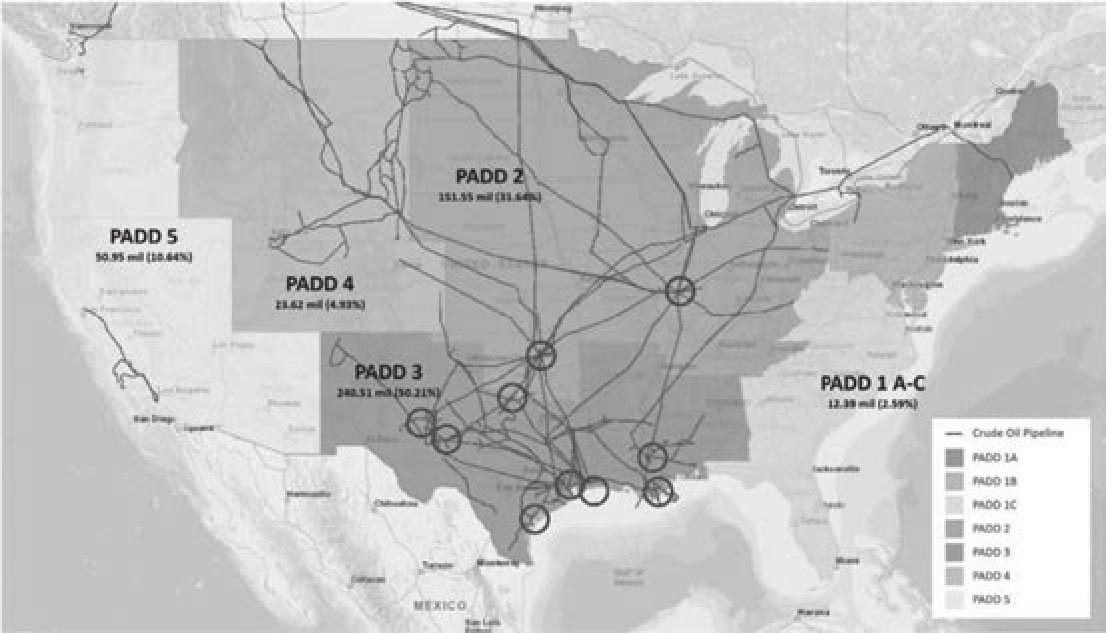
资料来源:Mukherjee et al.(2021)。
在找到少数对于石油库存而言至关重要的地点之后,接下来的问题就是寻找到能够让基于另类数据的预测值准确性随机变动的外生因素。和寻找枢纽相比,寻找这样的随机变量则要困难很多。Mukherjee et al.(2021)就此提出了第二个关键洞见:当云层遮挡的时候,卫星就无法再“看见”了。这样就有了一个直觉上很有创造性但是同时也很简单的识别策略(identification strategy)。如果卫星数据是有用的,那么以《另类数据:理论与实践》一书中第七章图7.11为例,在阴天的环境下,此时卫星无法“看到”某些对于宏观数据而言重要的石油枢纽,这样基于卫星形成的石油库存估计就存在着较大的误差,此时石油市场就需要等待政府报告来解决库存不确定性,从而后者就具有更多的信息含量并因此在发布时产生强烈的市场反应;反之当发布报告之前晴朗无云,那么卫星图像形成的石油库存就会更加准确,这个时候市场对政府报告的反应就会更弱。而如果卫星数据是无用的,也就是说资产价格已经反映了基于卫星形成的库存信息,那么无论是晴天还是阴天,市场对政府公告的价格反应都是相似的。考虑到天气的阴晴是随机的,这样只要卫星数据和其他数据形成的估计值在质量上的随机变动是不相关的,那么相对于资产价格中已经融入其他类型的信息,我们就可以识别出卫星数据的有效性。当然Mukherjee等人也指出,这种识别策略必须要在满足“排他性限制”的情况下才会成立,在当前选定的枢纽地区局部运量和石油库存的供给因素没有关系,否则识别策略就失效了。
进入实证分析的时候,作者使用了如下四组数据:
·十个枢纽地区的云量数据,它们来自于美国国家海洋和大气管理局(National Oceanic and Atomospheric Admininstration/NOAA)提供的综合地表数据库(Integrated Surface Database/ISD);[21]
·美国能源信息管理局(EIA)提供的石油库存数据;
·Oribital Insight基于卫星的每周石油库存数据;
·石油期货和期权市场的价格数据,包括西德州原油期货价格数据以及芝加哥期权交易所(CBOE)的原油隐含波动性指数(oil volatility index/OVX)。OVX指数是把标普500股指期权价格形成的VIX指数应用在美国石油基金USO期权上得到的。USO是一种ETF,它通过持有近期的石油期货合约和现金从而实现复制石油(WTI)价格的目的。
就识别策略的应用而言,我们需要定义“晴朗时段”(clear period)和“多云时段”(cloudy period)。因为EIA收集数据是在每周周五(测量日),而发布日期是在下周周三(公告日),这样如果从周五到下周三之间至少有一天是晴朗的,那么卫星就可以看清楚石油库存的情况,此时基于卫星的库存估计值就可以被市场看作是最新的准确库存信息,而政府在下周三公布的数据就成为过时的信息,市场亦将不做出反应。而如果从周五到下周三都是多云的天气,那么政府公告之前市场将无法获取库存信息,此时EIA周三公布的数据就成为最新信息,市场由此也会做出反应。出于这样的考虑,作者把每周四到下周二这段期间定义为“多云周”(cloudy week)或者是“晴朗周”(clear week)两类:如果在这段时间内每一天的云量都超过了一个临界值(样本的75%分位数),那么这段时间就被定义为多云周,否则就是晴朗周。[22]
有了多云周和晴朗周的定义之后,作者分析了下面的三个回归:
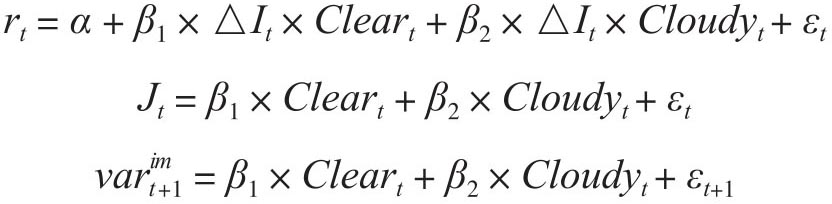
第一个是最主要的回归模型。左侧变量rt表示西德州原油期货近月合约在时点t的收益率,△It表示在时点t公布的原油库存非预期变化(也就是库存意外),它等于OI公司基于卫星的库存和EIA官方公布的库存之间差额绝对值和标准差之间的比率,这样这个指标的标准差就标准化为1,β1和β2可以分别解释为在晴天和阴天环境下石油库存意外每增加一个标准差所导致的回报率变动。Cleart和Cloudyt是两个哑变量,在晴朗周Cleart取值为1而Cloudyt取值为0;在多云周Cloudyt取值为1而Cleart取值为0。
第二个和第三个方程则是比较在基准时段以及之前时期美国石油库存关键枢纽地区上空的云层和石油市场不确定性之间的关系。第二个方程的左侧变量Jt表示在时点t出现的价格跳跃。这个指标沿用了Lee/Mykland(2008)在计算价格跳跃上采用的非参数方法。就价格跳跃而言,它通常和不常见的重要信息相关。当卫星能够提供有关原油市场的信息时,我们就可以预计多云周出现时价格将会发生比晴朗周更大幅度的跳跃,因为多云周意味着更大的不确定性。第三个方程沿用了相似的逻辑:如果卫星能够清楚“看到”石油库存,那么石油期权中反映未来油价不确定性的隐含波动率就更低。这样这个方程左侧变量就是在时点t+1的隐含石油收益率方差,它是从OVX指数中得出的。[23]
表4.7报告了上述这些回归的结果。其中A组报告了第一个回归方程在2014年1月到2018年12月这个基准时段的结果,[24]从中可以看到所有贝塔估计值均为负数,这反映了库存增加导致的过度供给和油价之间的负向关系。晴朗周的贝塔估计值都比较小,而且都没有统计显著性,这说明EIA公告遇到晴朗周时对油价几乎没有影响,由此意味着官方公告中的信息在发布的时候已经融入到油价中。与之相比,多云周的贝塔估计值要大很多,而且都是在1%的水平上显著。同时晴朗周和多云周贝塔估计值的差异也都在1%水平上显著。这些证据表明,近些年来晴朗周内的卫星库存数据和EIA的公告有关,因而导致后者对油价几乎没什么影响,但是多云周则不存在这种现象。B~D组报告的是针对第一个回归方程做的安慰剂检验(Placebo tests)的结果。其中B组报告的样本时段是2007年到2011年,此时石油市场参与者使用卫星数据还不是很普遍。C组报告的依然是基准时段中在EIA公告日的结果,但是计算收益率的时段延后两个小时。D组报告的是基准时段内非EIA公告日的收益率变动情况。B组的结果表明,在基准时段以前的时期,多云周和晴朗周内油价对于EIA公告没有明显的差异。而C组和D组的结果则表明,当延迟两个小时以及在非公告日的时段,油价不会对库存意外做出反应。E和F组是第二个回归方程的结果,它们表明在基准时段(第1/3列)中,当价格发生大幅跳跃的时候,多云周的系数要比晴朗周的系数高出25%左右,而且它们之间的差异具有统计显著性。但是在基准时段以前的时期,晴朗周和多云周的系数则没有明显差异。G组是第三个回归方程的结果,它的结果和E和F组的结果是类似的。
表4.7 油价在石油库存公告期间的波动
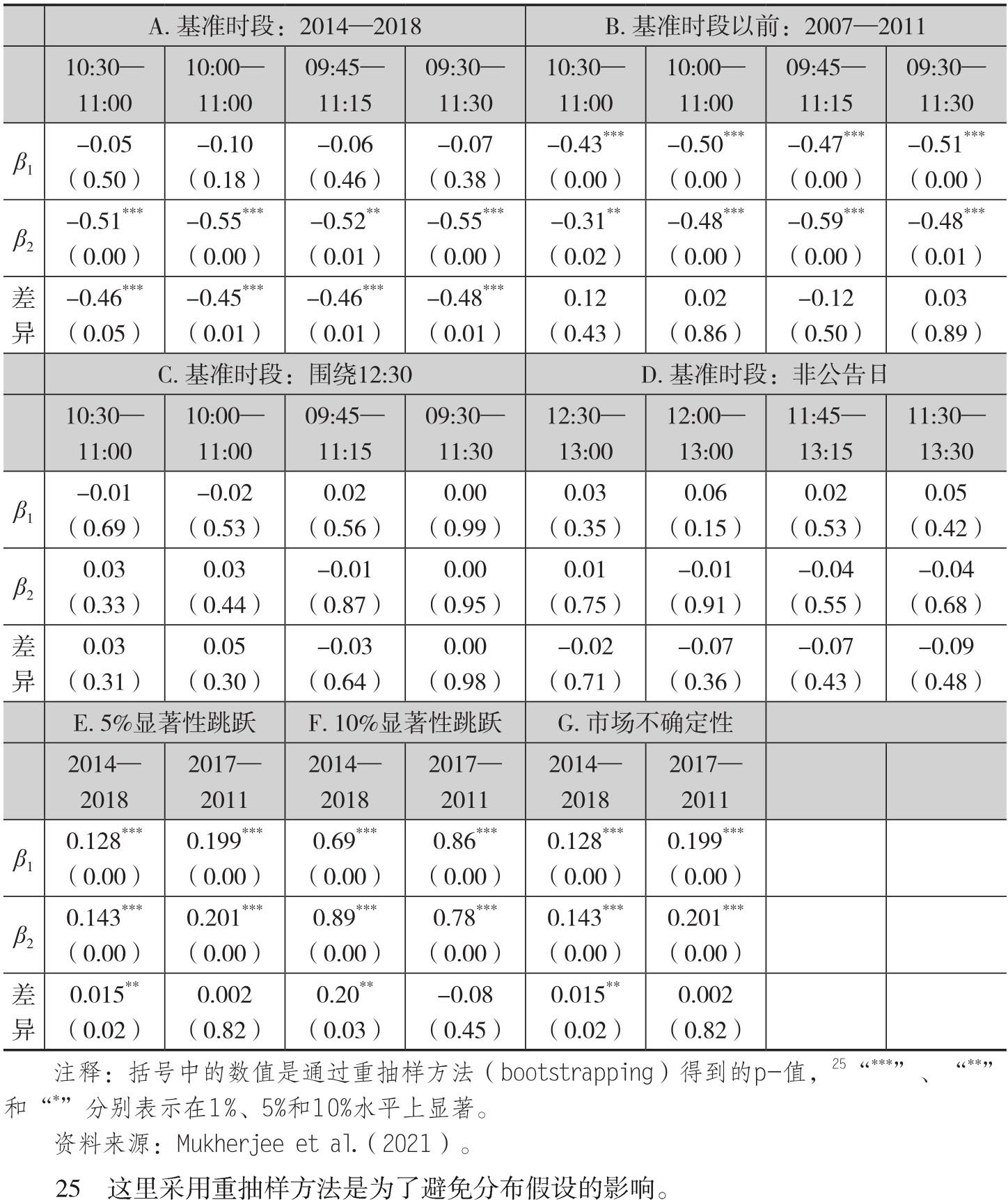
图4.5进一步对比了油价在基准时段和之前事前围绕EIA公告前后的价格模式。其中A图和B图分别报告了在基准时段和以前时期石油库存公告的价格影响,它们是通过不同时长的石油收益率对非预期石油库存进行回归得到的,这里计算石油收益率都是以早上9:30为起始时间,然后以15分钟为间隔延长计算收益率的时长,这体现在横轴的时间刻度上。图中的线1(2)反映的是晴朗周(多云周)的结果。C和D图则给出在基准时段和以前时期斜率估计值的差异,同时灰色区域表示估计值95%的置信区间。图中垂直的虚线时点是10:30分,这通常是EIA正式发布公告的时期。图4.5再一次证明了表4.5看到的结果,即在基准时段,油价针对库存公告的反应在多云周和晴朗周之间存在明显的差异,而这种差异在卫星数据尚未大规模应用之前的时期则不存在。
图4.5 石油库存公告和油价:基准时段和以前时期的对比
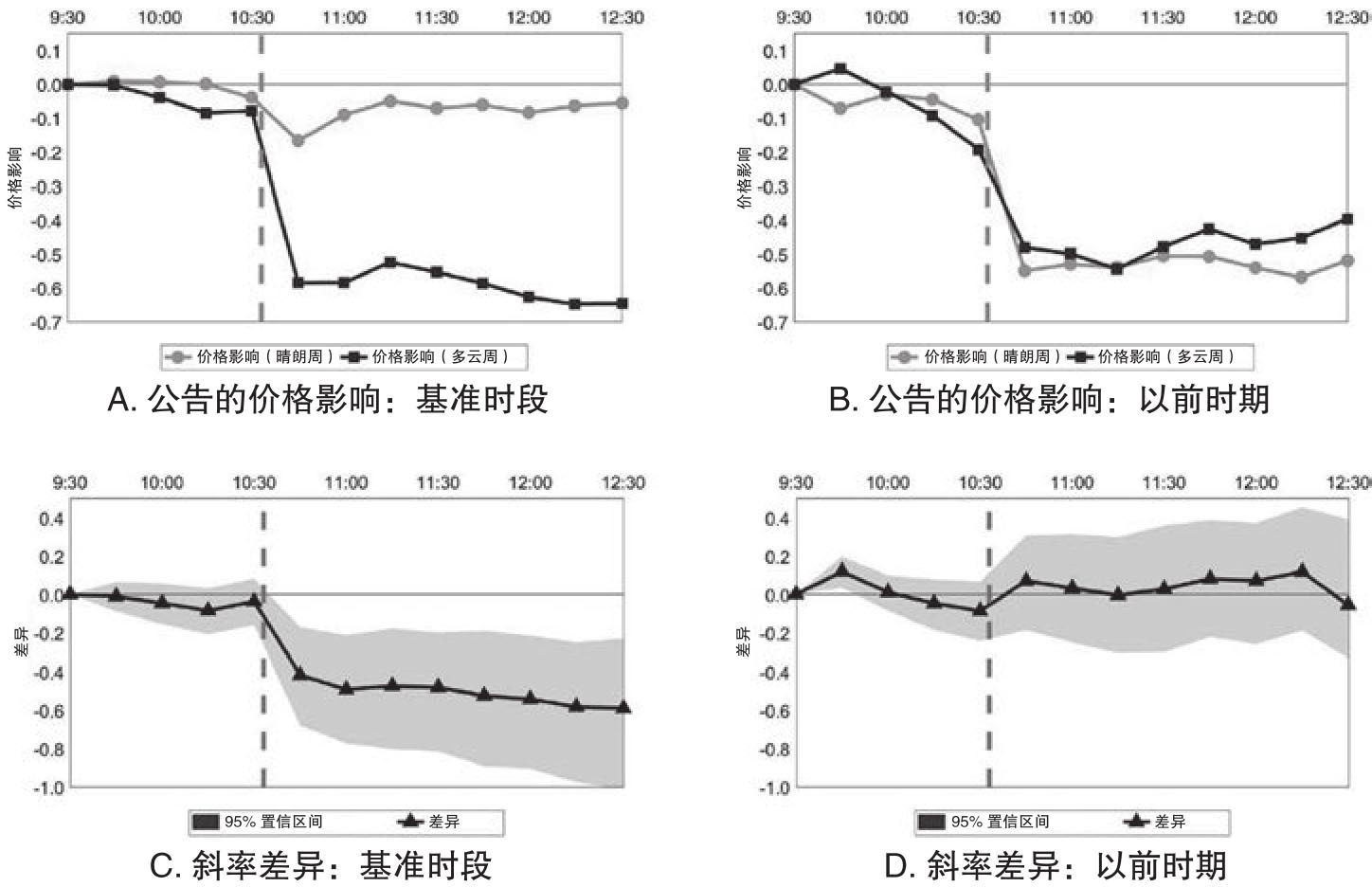
资料来源:Mukherjee et al.(2021)。
Mukherjee et al.(2021)这篇文章以翔实的证据证明了卫星数据在石油市场的应用价值,并且给基于卫星数据的市场择时策略提供了视角。在EIA公告前如果天气良好,这个时候可以根据卫星智能公司发布石油库存数据进行建仓,然后等到EIA正式公告的时候平仓;但是如果天气状况不佳,那么这种择时策略的价值就比较有限了。与此同时,在石油期权市场,当天气多云的时候未来油价不确定性程度较高,此时做多波动率的风险较小;而在天气晴朗的时候做多波动率的风险就比较大了。当然随着卫星技术的发展,如果未来也可以在多云的气象条件下准确估计石油库存,那么Mukherjee et al.(2021)的分析结论以及上述策略的绩效可能就要发生本质性的变化了。
