一、GDP
GDP一直是最为重要的宏观经济数据,它度量了一个国家或者地区的经济活动总量。Smith(2018)基于采购经理人指数(PMI)、经济景气指数(ESI)以及工业产值这些数据讨论了对GDP进行即时预测的可能性。
和GDP数据相比,PMI指数无疑具有更高的频率和时效性,因此可以用来跟踪GDP增长率的变动。图5.1刻画了欧元区GDP季度变化率和PMI指数之间的关系。从中可以看出,同时整合制造业和服务业的综合PMI指数能够正确显示在2008—2009年全球金融危机、2011年欧元区债务危机以及2017年经济回暖这些基本变化。
图5.1 欧元区GDP和综合PMI指数
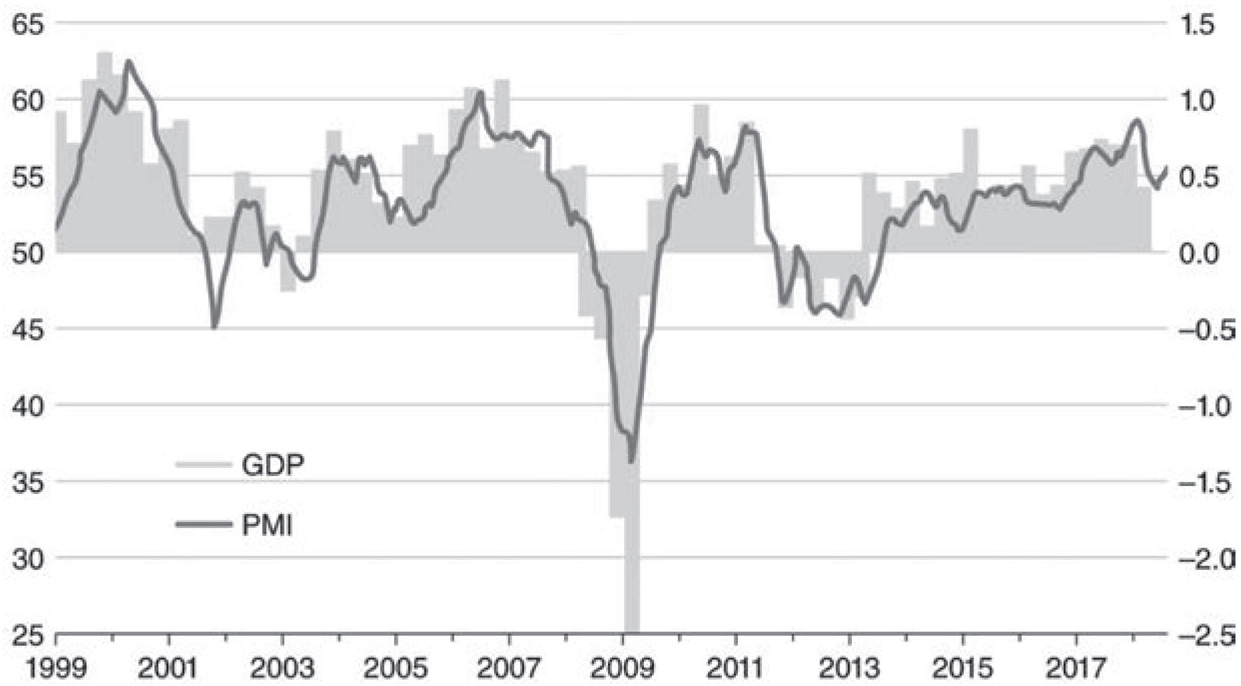
左坐标轴:欧元区综合PMI指数(埃信华迈发布)右坐标轴:欧元区GDP季度同比增长率资料来源:Smith(2018)。
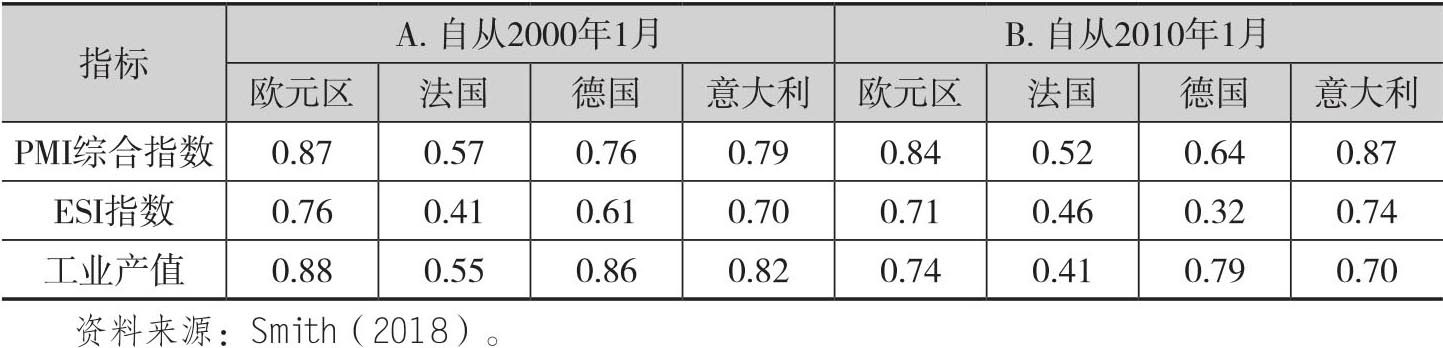
表5.1报告了欧元区及其三个最大成员国的GDP和PMI综合指数、经济景气指数(ESI)以及工业产值之间的相关系数。其中A组报告的样本时段从2000年1月开始,而B组报告了2010年以来的结果,这是为了避免2008—2009年全球金融危机的时段。基本上说,PMI指数和工业产值与GDP的相关程度差不多,同时这两组相关性都要比经济景气指数的相关性更高。在国家层面上,德国GDP和工业产值之间的关联性更强,考虑到德国的经济结构,这一点并不奇怪;就意大利而言,它的GDP和PMI指数的相关性很强;对于法国来说,PMI指数、经济景气指数以及工业产值和GDP之间的相关性都不强,虽然和PMI指数的相关性更强一些。
表5.1 GDP和一些指标的相关系数
我们知道PMI数据是每月发布一次,而GDP数据是季度发布的。为了在GDP的即时预测中解决一致性的问题,Smith(2018)采用了如下的自回归-混合数据抽样模型(autoregressiv-mixed-data sampling/AR-MIDS):
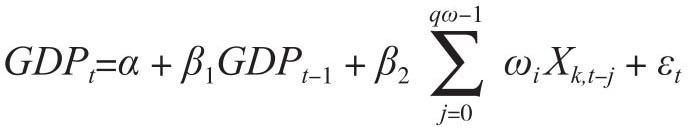
这样季度t的GDP是通过上一季的GDP以及其他自变量Xk,t以ωj为权重的加权平均加以预测的,这里k∈{1,...,m}是X在时段t内的观测值,同时m=3表示每个日历季度内记录的每月自变量的观测值。需要注意的是在这个模型中包含了j阶滞后项Xk,t-j,滞后阶数是由qω确定的。出于简化的考虑,这里使用了一个季度内的自变量的观测值进行预测,比如使用1月份、2月份和3月份的观测值来预测第一季度的GDP。
Smith(2018)分别使用PMI指数、ESI指数以及工业产值作为模型的自变量对2010年第一季度至2018年第一季度的GDP进行了样本外预测。[2]为了比较即时预测的结果,作者同时使用了均方根预测误差(root mean square forecasting error/RMSFE)以及准确预测GDP变化方向的比率这两个指标。同时作者还使用了一个基准模型(bechmarket model/BM),这个模型是一个简单不变的预测结果,即当前季度GDP增长率和上个观测值是一样的。表5.2报告了基于不同指标的模型预测绩效。
表5.2 不同即时预测模型的绩效
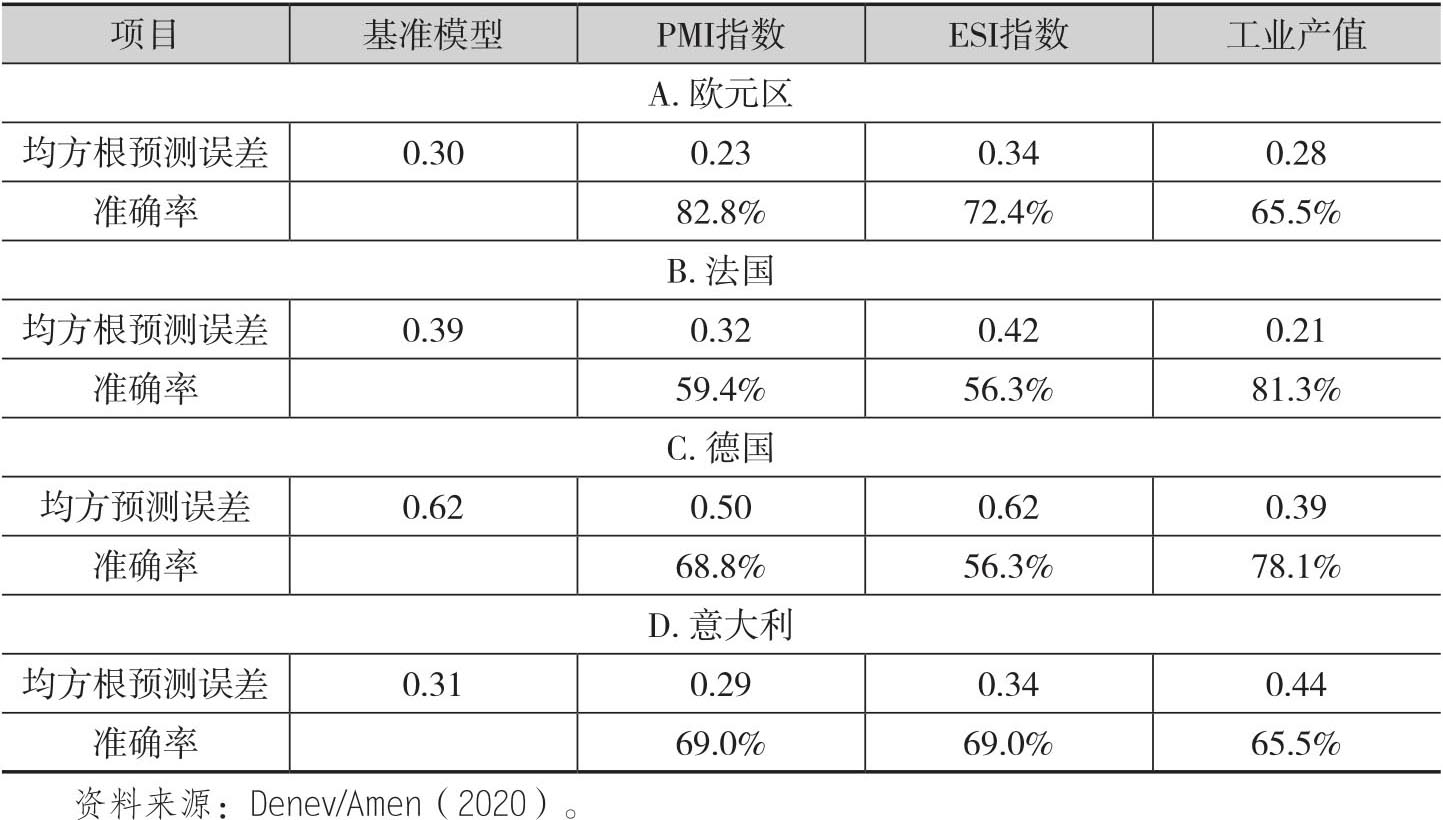
从上述结果中可以看出,包含PMI数据的模型在预测GDP同比增长率时通常要比ESI指数来得好。当考虑欧元区这个整体的时候,基于PMI的预测模型在均方根预测误差这个指标上要明显好于基于ESI指数和工业产值的预测,同时要比基准模型的绩效高出25%左右。同时PMI模型在超过80%以上的时段内准确预测了欧元区GDP季度增长率的方向,而这个预测绩效也要强于基于ESI和工业产值的预测。在法国、德国、意大利三个国家中,基于PMI的模型依然强于基准模型和基于ESI的模型,但是基于工业产值的模型在均方根预测误差和方向准确率这两个指标上都表现更高。[3]而在意大利,只有基于PMI的模型在均方根预测误差上的绩效优于基准模型。
