数学是形与数的高度统一
二、数学是形与数的高度统一
现实世界,是物质世界。我们所看到的、所面对的、所接触到的万物,无不以形示人。而“万物皆数”,形与数是紧密结合、内外一体的。数学,则正是以空间形式和数量关系为研究对象的科学,而且是将形与数高度统一起来进行研究的学科。
人类认识数(识数),是人类进化的一大标志。在远古蛮荒时代,人们通过渔猎所获得的食物很少,不需要计算它们的数量。而随着人类劳动能力的提高和社会的进步,获得食物较多,才逐渐产生数量概念,产生计量和计数的需要。所以数和计数,是人类进步的重要标志。最初,“数(shù)”是从人们对食物等(例如野物、石子)用手指“数(shǔ)”出来的。
“万物皆数”是古希腊毕达哥拉斯学派提出来的,也是他们坚信不疑的信条。其原因是,他们认为数是万物内在的本质。无论什么物质,都会随时间变化而变化。如打到的猎物,吃掉了,就不再存在了,然而他们仍然记得他们曾经打到过多少猎物;那些猎物的数目,是不会消失的。进一步,若是曾用某些符号记录过那些猎物的数目,那么就更有依据了。

图2-2-1 泰勒斯(前624—前547)
古希腊以几何为数学,以泰勒斯、毕达哥拉斯为代表的数学家,热衷于几何学研究。但他们寓数于形,把形与数结合起来,不仅仅研究几何图形的特性,也研究数。特别是关于无理数的发现,最为精彩。
毕达哥拉斯学派所说的“万物皆数”的“数”,实际上是专指正有理数,即正整数和正分数。数有最小的单位,其他数则都是它的倍数。把数按其大小,排列在直线上,相当于现在所说的“数轴”,一个数对应于直线上的一个点。他们称此直线为数直线(实际上是有理数数轴的正半轴)。他们认为数直线是有限可分的,直线上有最小的原子。所以毕达哥拉斯学派是“原子论”者。在此数直线上,只有代表正整数和正分数的点,即有理数的(有理)点。这条数直线,实际也不是完整的数轴(没有负半轴,也没有无理数对应的点)。
在这种“原子论”的观点下,他们认为任何两条线段,都是“可公度”的。即可以互相辗转相除的,可以互相量尽的。因为任何线段(的长度)都是最小“原子”的倍数,所以任何两条线段都有公共的倍数(以线段表示的公倍数),因此一定是“可公度”的。这是当时毕达哥拉斯学派的一种信条。
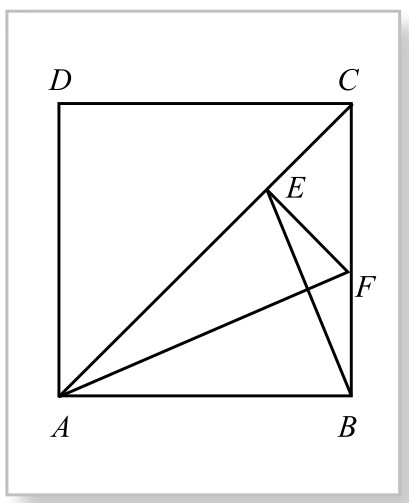
图2-2-2
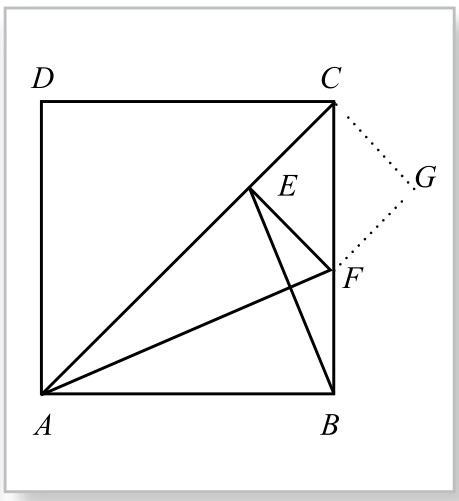
图2-2-3
但是,该学派中有个叫希帕苏斯的成员,发现正方形的对角线与其一边却不可公度。事实上,如图2-2-2所示,在正方形ABCD中,用一边AB来量对角线AC,使AE=AB,剩余为CE。作∠BAC分角线AF,交BC于F,连接AF,则易知△AEF≌△ABF(SAS),而有EF=BF,且∠AEF=∠ABF=90°,于是∠CEF=90°。又因∠ECF=45°,故∠EFC=45°, CE=EF, △CEF为等腰直角三角形,于是CE与CF又成为另一个小正方形CEFG的一边与对角线,如图2-2-3所示。因此,又回到原来的问题:用正方形的边来量它的对角线。如此便出现循环往复,以至于无穷的困境。也就是说,正方形的边与对角线,二者不存在公度线段,即正方形一边与对角线是不可公度的。
因为每一次公度,都只能产生一个(有理)数。现在发现有不可公度的两条线段,亦即发现了一种新数——竟然不是(有理)数。这便动摇了该学派“万物皆数(有理数)”的基本信条。据说为了维护学派的基本信条,信徒们便把这种“怪数”的发现者希帕苏斯,投入大海淹死了。这成了科学史上第一个冤案,并由此而引发“第一次数学危机”。但正是由于无理数的发现,使数域突破了有理数的藩篱,人们认识了实数的存在,使数学向前迈进了一大步。
可见,无理数(实数)正是在形数结合研究的过程中诞生的。
黄金分割和黄金数,又是一个形数结合产生的奇花异果。所谓黄金分割,是一个几何作图问题:在一条线段AB上作分点D,使AB分为大小不等的两段(AD>DB),而使全段与大段之比,等于大段与小段之比(故也称为中外比),即AB∶AD=AD∶DB,或者说使大段为全段与小段的比例中项:AD2=AB · DB。
如果设AB=1, AD=x,便有x2=1·(1-x),从而有x2+x-1=0,解得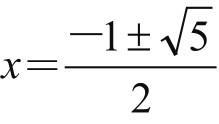 (只取正值)。据此,可以设计作图方法如下:以AC=1, BC=
(只取正值)。据此,可以设计作图方法如下:以AC=1, BC=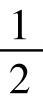 为两直角边,作Rt△ABC,如图2-2-4所示,则有:AD=AE=AB-DB=
为两直角边,作Rt△ABC,如图2-2-4所示,则有:AD=AE=AB-DB=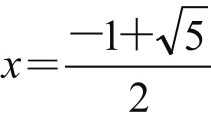 。
。
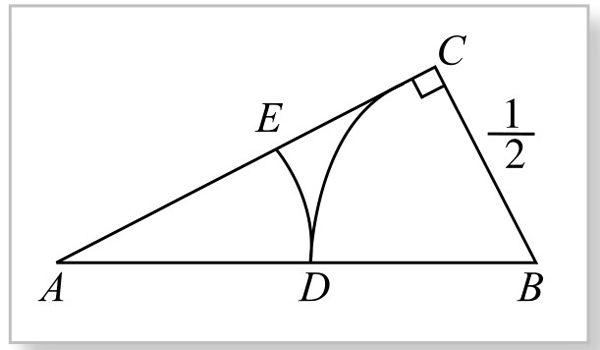
图2-2-4
E点称为线段AC上的黄金分割点。ω=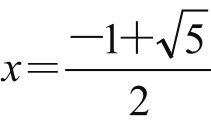 便是黄金数(或黄金比),取其三位(实际是四位)小数近似值,便得ω=0.618。它在欧洲中世纪的绘画、建筑和很多方面都有重要的应用,所以获得“黄金数”的美名。
便是黄金数(或黄金比),取其三位(实际是四位)小数近似值,便得ω=0.618。它在欧洲中世纪的绘画、建筑和很多方面都有重要的应用,所以获得“黄金数”的美名。
由上式可得x(x+1)=1, 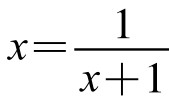 ,若将分母中的x用其分式表示式带入,便得一繁分式,再一步步迭代,便得到黄金数的连分数表示式:
,若将分母中的x用其分式表示式带入,便得一繁分式,再一步步迭代,便得到黄金数的连分数表示式:
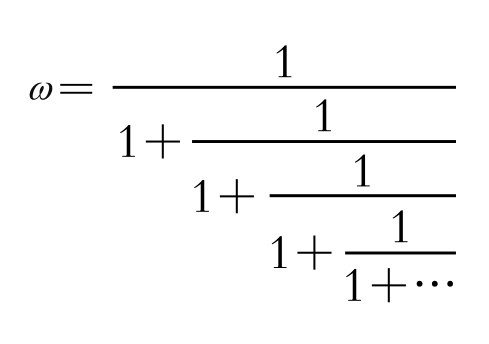
将其无限尾部弃掉,便可以得到它的近似分数: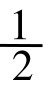 ,
, 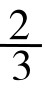 ,
,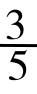 ,
,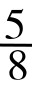 ,
,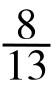 , …若将其分子排成一列,即得:1, 2, 3, 5,8,13, …这便是著名的斐波那契数列。这在后面还会详谈。黄金数与斐波那契数列,在优选法的应用中大显身手,是优选法的数学理论基础。
, …若将其分子排成一列,即得:1, 2, 3, 5,8,13, …这便是著名的斐波那契数列。这在后面还会详谈。黄金数与斐波那契数列,在优选法的应用中大显身手,是优选法的数学理论基础。
形数结合的例子,比比皆是。以后我们还会见到很多。万物运行,皆有自然规律,而自然规律无不可以用数学公式表述。这便是“形中有数,以数表形”的根本原因。
