关于三角形界心的妙论
五、关于三角形界心的妙论
(一)关于三角形界心的三个定理
1999年,重庆市第十六中学的夏培贵老师,在《中学数学教学》上发表《关于分周线的三个定理》,提出三角形分周线及有关的三个几何定理。一时引起很多人的关注。
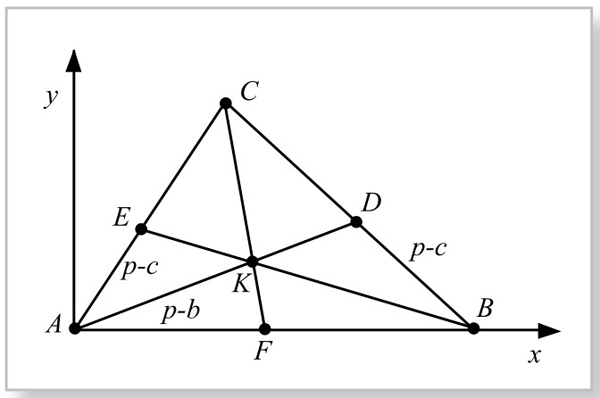
图5-5-1
所谓三角形的“分周线”,是指△ABC周边上两点D、E,若它们将三角形周长(三边之和)分成相等的两部分,那么直线DE就称作该三角形的一条分周线。显然,任何一个三角形,都有无穷多条分周线。但是通过三角形边上固定的任意一点(包括顶点),有且只有一条分周线。特别地,通过三角形的三个顶点,有三条分周线;通过三边中点也各有一条分周线。夏培贵老师文章中的前两个定理,就是说通过三角形三个顶点的三条分周线交于一点——称为第一等周中心(界心K);通过三角形三边中点的三条分周线也交于一点——称为第二等周中心(界心J)。“定理3”是最有趣的结论,我们称之为三角形界心定理:任意三角形的第一界心K、第二界心J与三角形重心G,三点共线。这是一个非常困难的几何证明题。由于没有发现纯几何证法,夏老师文中用的解析方法,以繁代难。虽然解析证明十分复杂,但他通过复杂的计算,终于给出了这个定理的证明。整个定理的解析证明,用了整整两页的漫长篇幅。
他在事先证明定理1、2时,以A点为原点,以AB为x轴正向,建立直角坐标系(图5-5-1)。设三角形三边长分别为a, b, c;设p为三角形半周长,则可求得点K、J的坐标,分别为:
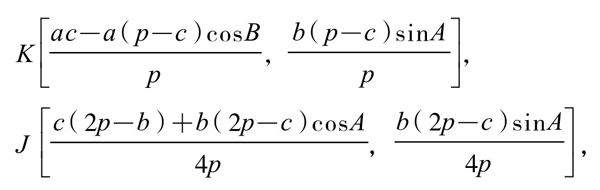
△ABC重心坐标为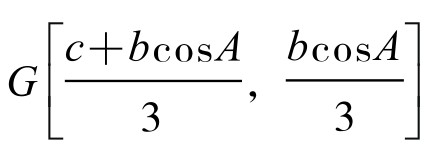 。
。
欲证K、J、G三点共线,只需证明直线GK与KJ的斜率相等。他通过复杂的计算,得
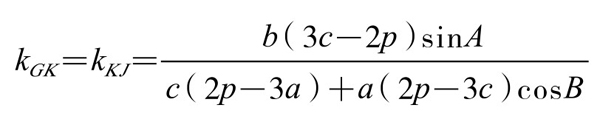
因此,G、J、K三点共线。
夏老师发现这三点共线,是很不容易的,是十分有价值的成果。但是美中不足的是用解析方法,计算过于烦琐。如果能有简化证明就更好了,特别是能够发现几何证法,就完美了。果不其然,文章发表不久,就有两篇稿子给出了不同的简化的几何证明。特别是陈传孟老师的纯几何证法,非常简洁,非常精彩,而且还丰富了原有结论。下面就来看陈老师精彩的新证明方法。
(二)漂亮的几何证法
在“陈证”中,将三角形的等周中心,称为三角形的“界心”。先证第一界心J(上述的K点)存在。即从三角形三顶点出发的分周线共点。从图5-5-2上看,直线BJE截△ACB,由梅涅劳斯定理知: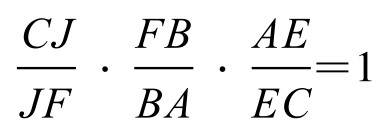 。若设三边AB=c, BC=a, AC=b, p为半周长,则AF=CD=p-b, BF=CE=p-a, AE=BD=p-c,从而
。若设三边AB=c, BC=a, AC=b, p为半周长,则AF=CD=p-b, BF=CE=p-a, AE=BD=p-c,从而
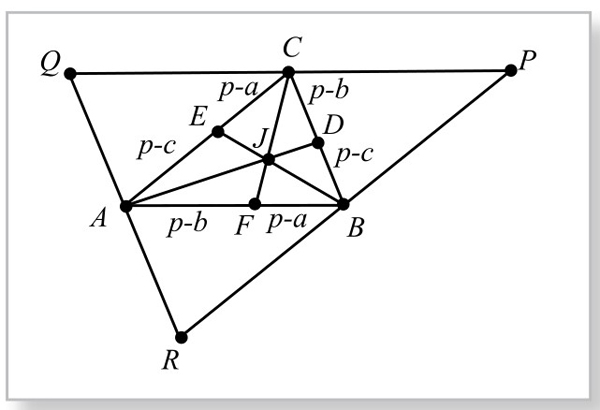
图5-5-2
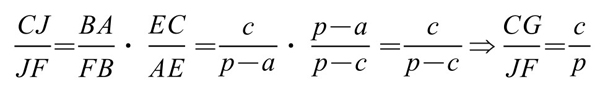
过A、B、C分别作对边平行线,交成△PQR,如图5-5-2。且设J到PQ、PR、QR距离分别为lC, lB, lA;J到AB的距离为hc,则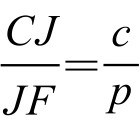 。因此,
。因此,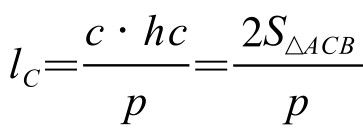 。
。
同理可证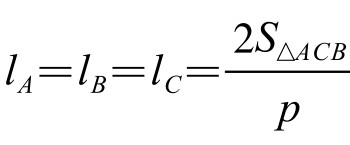 。
。
此为定值。这就是说J点到△PQR三边等距离,故知J点即为该三角形的内心,因而肯定是存在而且唯一。而且因为△PQR与△ABC逆对称,对称中心为两个三角形的共同重心G,故知△PQR与△ABC的内心J与I,是关于G点为中心的逆对称点,应在同一条直线上,即J、G、I三点共线。(这是得到的副产品。)(https://www.daowen.com)
再证第二界心K(即前述J点)存在。
如图5-5-3,设△ABC的三边中点分别为D、E、F, DS、ET、FU为三条等周线。则由AF=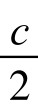 , AE=
, AE=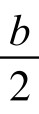 ,而AF+AE+EU为半周长,知EU=
,而AF+AE+EU为半周长,知EU=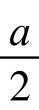 =EF(△ABC中位线),又因为DF∥AC,故有∠EFU=∠EUF=∠DFU,因而FU为∠DFE分角线。同理。可证SD、TE分别是∠EDF、∠DEF分角线。因此,这三条等周线DS、ET、FU交于△DEF的内心K,即K点也是唯一存在的。但显然△DEF与△ABC也为逆对称,其对称中心也是二者的公共重心G,故此两个三角形的内心关于G点为逆对称点,即K、G、I在一条直线上。
=EF(△ABC中位线),又因为DF∥AC,故有∠EFU=∠EUF=∠DFU,因而FU为∠DFE分角线。同理。可证SD、TE分别是∠EDF、∠DEF分角线。因此,这三条等周线DS、ET、FU交于△DEF的内心K,即K点也是唯一存在的。但显然△DEF与△ABC也为逆对称,其对称中心也是二者的公共重心G,故此两个三角形的内心关于G点为逆对称点,即K、G、I在一条直线上。
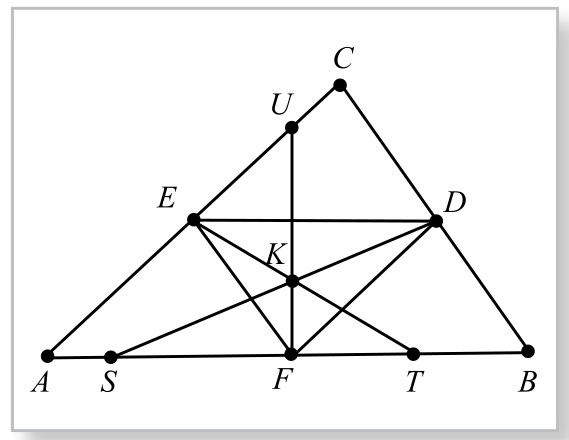
图5-5-3
如上述所证,知J、K都在直线GI上,或者说四点J、K、G、I共线。而且由于△PQR与△ABC逆对称,△ABC又与△DEF逆对称,且相似比都是-2。故知这四点不仅在一条直线上,而且其位置有固定距离关系:JK∶KG∶GI=3∶1∶2。
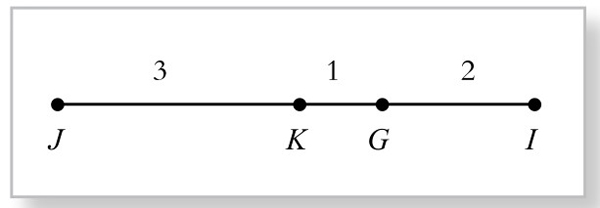
图5-5-4
这四点所共在的直线,是一条有关三角形的特殊点共线的直线,完全可以与“欧拉直线”(三角形外心、垂心与重心共线)相媲美。
关于界心的上述定理,两种证明方法相比较,解析法繁杂,但有成套的计算办法(坐标几何);而纯几何综合证法简洁漂亮,但很难想得到。当遇到困难,而又暂时无法可想时,以繁代难,未尝不是个好办法。但在有了繁杂证法之后,又要想办法化繁为简。这是我们在遇到难题时,分两步走的通常想法。这也是数学难题求证(或求解),给我们的启示之一。而这里所展示的几何证明方法,实在是巧妙,看了此证明之后,我们的心灵实在是感到了美的享受!
(三)历史回望
以上关于三角形界心的三个定理,及其漂亮的证明方法,确实给了我们一次数学美的欣赏。但是,早在百年之前,就已经有人进行过类似的研究,并且有过类似的发现。
19世纪后半叶至20世纪初叶,包括布洛卡(Brocard,1845—1922)、莱莫恩(Lemoine,1840—1912)、约尔刚(Gergonne, 1771—1859)和奈格尔(Nagel,1821—1903)在内的一大批数学家,掀起过一阵研究欧氏几何的热潮,获得了不少新成果。有多部著作对此有过较为系统的总结。但是,这些著作均离我们较远,而新译又出版较迟,所以一般人并不知道其中的内容。所以在近十年中,早在一个世纪以前就已经获得的结果,又被重新“发现”。人们对“布洛卡点”的兴趣,就是一个例子。而对“界心”的兴趣,是另一个例子。
我们现在就来看一看,上述著作中关于这方面有些什么主要成果:
1.△ABC内切圆切三边于D、E、F,则AD、BE、CF相交于一点M,这一点称为Gergonne点;
2.△ABC旁切圆切三边于P、Q、R,则AP、BQ、CR相交于一点N,这一点称为Nagel点;
3.△ABC的Gergonne点和Nagel点为一对等距共轭点;
4.△ABC重心G、内心I和Nagel点N共线,且GN=2IG;
5.设S是IN的中点,则S是△ABC中点三角形△O1O2O3的内心,△O1O2O3的内切圆称为Spieker圆。
联系现实,回忆历史,我们可以得到以下一些结论:
第一,△ABC的第一界心J,就是Nagel点。
事实上,在△ABC中,若D、E、F分别是三边BC、CA、AB上内切圆的切点,显然,AD、BE、CF是分周线。故它们的交点——Nagel点,即是第一界心J。只是在Nagel的时代,还没有“界心”这个概念,因此,也没有人指出这一点。
第二,△ABC的第二界心K,就是Spieker圆的圆心S。
事实上,△ABC的第二界心K,是内心I和第一界心J的中点,与Spieker圆的圆心S的定义一致,即点J就是S。不过,那时也许没有人注意S点具有第二界心的性质。现在夏先生等人从“界心”这一概念出发,指出了这一点。真可谓纵然相隔百年,但英雄所见略同。或者说“老树春来又发花”。
