四、欧拉与七桥
四、欧拉与七桥
(一)七桥问题引发图论诞生
18世纪东普鲁士的哥斯尼堡(现为俄罗斯的加里宁格勒),有一条帕瑞格河流经城区,河上有两个小岛,有七座桥把两个小岛与河岸联系起来,如图4-4-1所示。
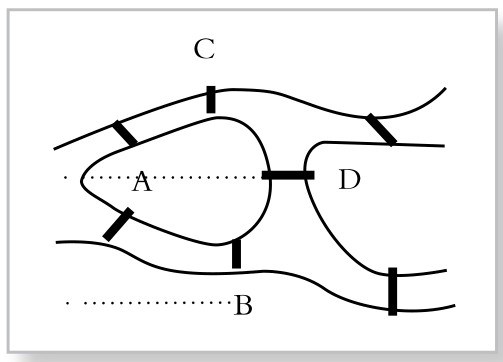
图4-4-1
傍晚,人们经常在桥上散步。于是有人突发奇想,提出一个问题:一个人能否一次性地走过这七座桥,而每座桥只走一次,最后回到出发点?这个问题一经提出,立即引起许多人的兴趣。大家都在散步时试一试,以求解决这个问题。但是,走来走去,人们始终找不到一条散步路线,能够一次性地走过这七座桥而不重复过桥,并最后能回到出发点。是没有找到这条一次性路线呢?还是根本就不存在这样的路线呢?大家无法解决这个难题。于是人们请教大数学家欧拉。

图4-4-2 欧拉
欧拉运用数学抽象的方法,巧妙地解决了这一难题。他的想法是:人们能否一次性走过七座桥,与每座桥的长短、形状都没有关系,与每块陆地的大小也没有关系。因此,可以把河的两岸和小岛等四块陆地,缩小到一点;把每座桥拉长,使其变成一条连接两点的曲线。即令图4-4-1变成由四个点和七条线组成的图4-4-3。能否一次性走过这七座桥,就变成:能否一笔画出这个图来,而不重复。这样,就把一个实际问题,变成图形一笔画的数学问题。欧拉解决了这个问题,同时开创了数学的新分支——图论。
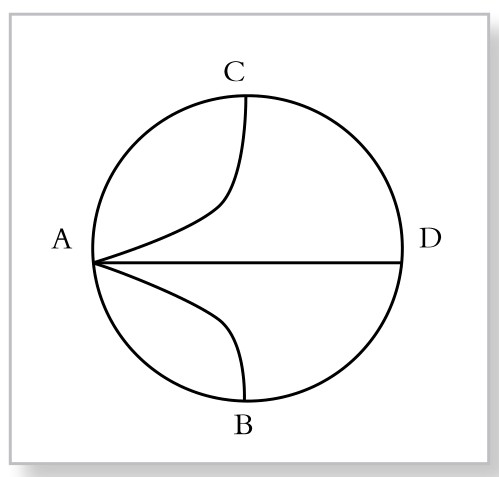
图4-4-3
为了解释方便,把图中的点,称为“顶点”;图中的线条,称为“边”。连接偶数条边的顶点,称为“偶顶点”;连接奇数条边的顶点,称为“奇顶点”。
假如一幅图能够一笔画成,那么,除了起点和终点以外,其他顶点(中间点)都是一条边进,一条边出,因此都应该是偶顶点;只有起点和终点可能例外。所以,如果一幅图上的顶点没有奇顶点,或最多只有两个奇顶点,那么,该图就一定可以一笔画成。否则,就不能一笔画成。这样,就得到判别“图”能否一笔画的准则:若其奇顶点数目不超过2,则可以一笔画成;否则不能一笔画成。
现在,我们回到七桥问题。这只要看图4-4-3上的奇、偶顶点的个数就行了——图上的四个顶点,都是奇顶点,个数超过2,因此它不能一笔画成。从而图4-4-1中的七桥,人们不可能一次性走过每一座而不重复。人们长期以来的困惑得到了解决。为了纪念欧拉,人们把能够一笔画成的图,称为“欧拉图”。
通过欧拉解决七桥问题,我们看到了数学的力量:它可以将一个十分困难的实际问题,抽象成一个图形问题,在纸上通过图解就能得出答案。
(二)管梅谷与中国邮路问题
一个城市,以街道为边,以两条街道的交点为顶点,并以每条道路的长度标数,便组成了一幅加权图(标注每边长度)。邮递员需要走过每一条街道和每一个交点。问:如何选择一条最短邮路,使邮递员从邮局出发,跑遍所有的街道送完信以后,再回到邮局?这是中国数学家管梅谷先生于1960年在国际上首先提出来的邮递员问题,被国际图论界命名为“中国邮路问题”。
在“图”的每条边上加注数字表示边长,就成为一幅加权图。图中若干点和边连接起的折线,称为链。图中一条链上各边长之和,称为该链的长度。一条链的起点和终点重合为一点,则称为一条回路。
一幅加权图中的“最短邮路”,要符合以下条件:(https://www.daowen.com)
1.是可以一笔画成的“最短邮路”,不过可能有些边有重复;
2.没有多于两次以上重复的边;
3.图中每条回路上重复边的总长度,不超过该回路长度的一半。
满足这些条件的“最短邮路”,称为“中国邮路问题”的最优解。
关于最优解问题,有以下结论:
中国邮路问题的最优解是存在的;如果存在两个满足条件的最优解,那么它们邮路的长度相等。
以下我们用实例来介绍求最优解的方法。
问题:设邮路是如图4-4-4所示的加权图,其中点A是邮局所在地,每条线段上所标出的数字,表示该路段的长度。求此邮路的最优解。
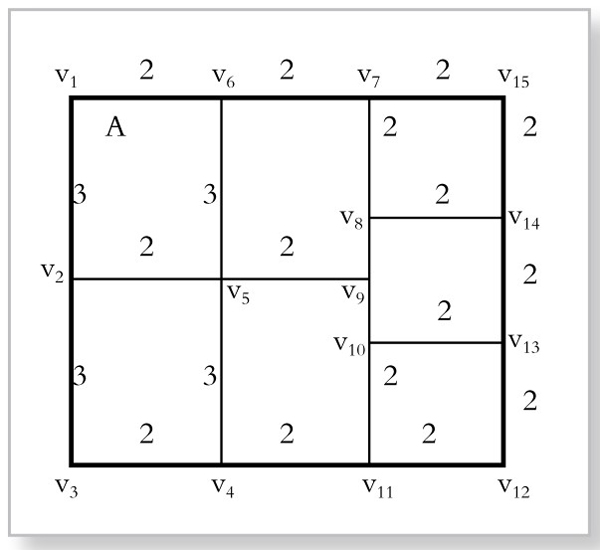
图4-4-4
这是一幅有15个顶点的加权图,因为有10个奇顶点,所以它本身不能一笔画成。要想使它变成欧拉图,就要消灭这10个奇顶点。
我们注意到:若在两个奇顶点之间加一条边(重复边),就可以将这两个奇顶点消灭,使得奇顶点变为偶顶点。例如,在V6、V7之间加一条边,这两个顶点就变成了偶顶点。所以在加若干条边之后,就可以消灭所有的奇顶点,而使加边以后的图成为欧拉图(包含重复边)。在两个顶点V6和V7之间加一条边,其实际意义就是:在这长度为2的边V6V7对应的街道上重复走一次。因此,我们在造就加边欧拉回路时,希望所加的边越少越好,所加边的总长度越小越好。
下面用两种方法来加边,如图4-4-5、4-4-6所示。图4-4-5中的加边欧拉回路,在每个回路上的长度总和不超过所在回路长度的一半,符合最优解的条件,故这是一个最优解。图4-4-6中所加的边,在回路L1、L2上的长度之和,已经超过了所在回路长度的一半:回路L1的长度为8,所加边的长度为6;回路L2的长度是10,所加边的长度为6。所以图4-4-6中所画的加边欧拉回路,不是最短回路,因此,它不是最优解。现在,我们将图4-4-6中的加边回路进行调整,如图4-4-7所示。
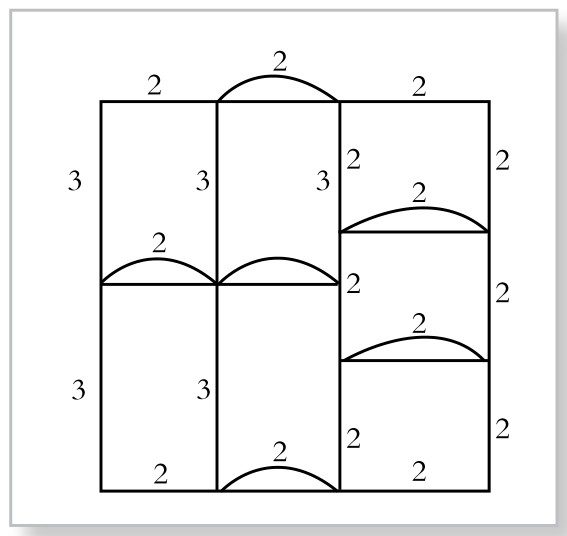
图4-4-5
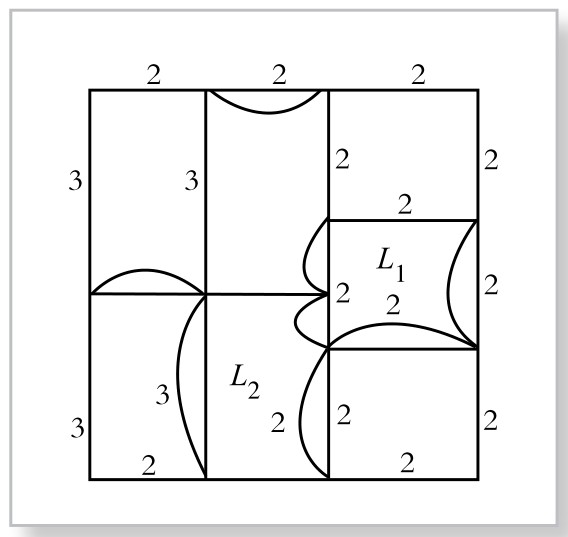
图4-4-6
经过检查可知,图4-4-7中的加边欧拉回路,符合最优解的条件,因此,它也是一个最优解。而且,可以检验:它与图4-4-5中的邮路的总长度相等。
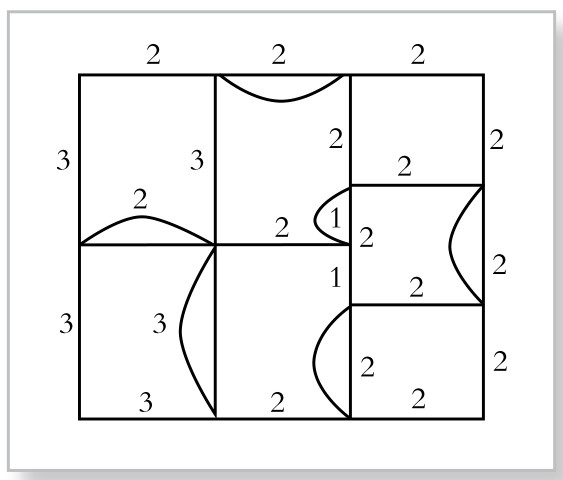
图4-4-7
