表上作业解决逻辑问题的诀窍
十三、表上作业解决逻辑问题的诀窍
数学的抽象性,使得问题的数学解决,很难有固定的模式和固定不变的方法。在运用数学方法时,有时要辅以其他非数学方法,特别是在寻求解决的思路时更是如此。例如有些逻辑问题,没有既定的思路,如果只靠逻辑推理,很难找到问题的切合点。在实际经验中,列表是个有效的好办法。请看下面这个问题。
例1.A、B、C、D四人赛跑,在比赛前,甲、乙、丙三人对他们的成绩进行预测:
甲预测:A——第一名,C——第三名;
乙预测:B——第一名,D——第四名;
丙预测:D——第二名,A——第三名。
比赛结果的名次,甲、乙、丙三人每人的预测皆一对一错,而且每个名次皆有人猜对。现问:A、B、C、D四人的名次究竟如何?
解这类逻辑问题的一个有效的方法是列表法,并在表上进行操作。先将甲、乙、丙三人的预测资料输入表中(表5-13-1):
表5-13-1
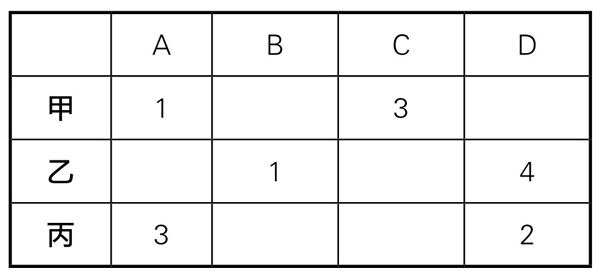
因为每人所猜名次一对一错,故甲所猜的A——1, C——3中有一个对,有一个错。哪个是对呢?
(1)假设A——1猜对(在表上画“√”),那么C就不是第三名(在表上画“×”);A也不可能是第三名,所以,丙猜A第三名——错(画“×”),则丙猜D第二名就应该对(画“√”);那么D不可能是第4名(画“×”),于是B是第一名(画“√”)。到此表中有两个第一名,出现矛盾。所以这种假设不成立。这一过程被称为“表上作业”。所得表上作业的结果,如下表5-13-2所示:
表5-13-2
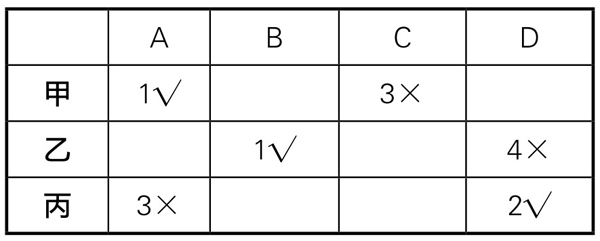
可见,A不是第一名。
(2)假设C是第三名,那么,A非第一名;A也非第三名,D第二名;从而D非第四名,于是B第一名。如表5-13-3所示:
表5-13-3
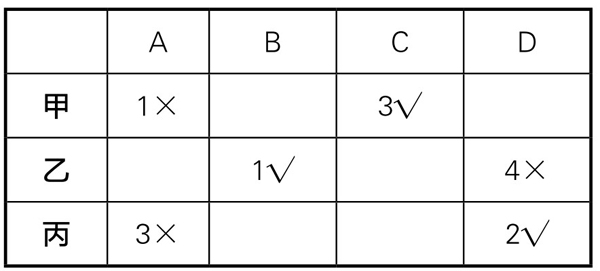
由此推得:B第一名,D第二名,C第三名,A第四名。
若问:如果甲、乙、丙三人中有两人全猜对,一人全猜错,那么最终名次如何呢?请有兴趣的读者,仿照前法予以推断。
例2.(表演题)问题如下:
请您阅读下面的脚本,并在□内分别填写数字1~5中的某一个。
[脚本]
道具:A、B、C、D、E每人手里拿一张纸片,上面分别写有数字1、2、3、4、5,纸片上的数字只有拿它的本人看得到,小明对此一无所知。
表演:教师与学生A、B、C、D进行如下对话,小明则只在一旁听,并不插话。问答如下:
T问A:谁的数字最大?
A答:不知道。
T问B:C同学的数字比你的大吗?
B答:不知道。(https://www.daowen.com)
T问C:D同学的数字比你的大吗?
C答:不知道。
T问D:B同学的数字比你的大吗?
D答:——①是;②不是;③不知道。
T再问B:C同学的数字比你的大吗?
B答:不!
T问小明:听了我与同学们的问答后,你知道各人纸片上的数字是什么了吗?
M:知道。他们纸片上的数字分别是:
A□;B□;C□;D□;E□。
T:很好!你说得对。
说明:这是日本的一道低年级学生数学奥林匹克竞赛题,是道很有意思的逻辑思维表演题。整个问题的文字很长,是在叙述一场数字游戏的全过程,而问题则含在游戏表演的过程之中,而要求的结果——在方格中填写适当的数字(1, 2, 3, 4, 5中的某一个)。问题形式新颖,虽然是逻辑推理问题,但很有趣味性。我们可以用表上作业的方法来进行分析和解决。
分析和求解:在教师与学生A、B、C、D的问答中,隐含了如下信息:
(1)因为A不知道谁的数字最大,说明他的数字不是5(否则他自己最大);因为B不知道C的数字是否比他大,所以他的数字既不是5,也不是1;同理,C的数字也不是5和1。但是如果只将这些信息记在脑子里,便搅在一起,不能很好地利用这些信息进行下一步推理。现将这些信息填入表5-13-4中(如被否定,则在相应的格子里画记号“\”),便能够方便地帮助我们进行进一步思考和推理:
表5-13-4
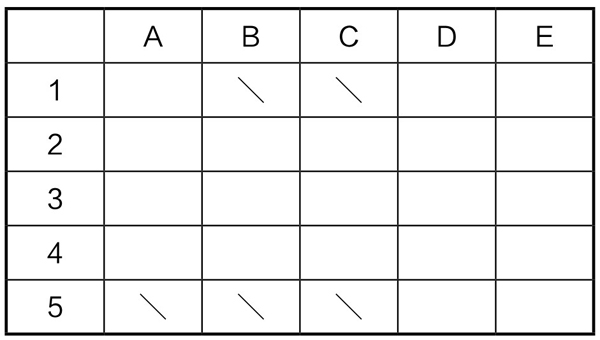
(2)教师问D, D的回答有三种选择,分别来进行推理。我们的目的是,通过D的回答能决定出D手中卡片上的数字是几。
1.若选①,则B的数字比D大。
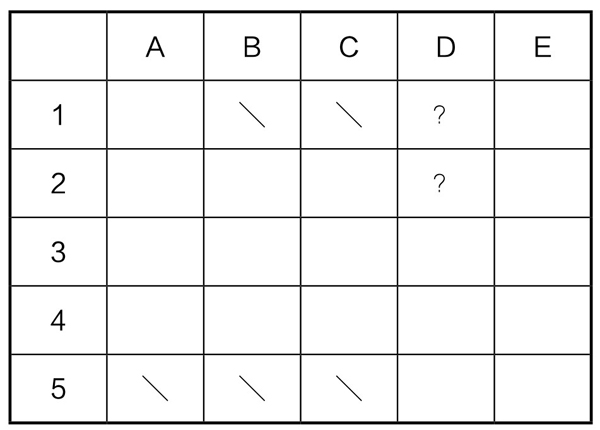
在D知道B的数字已经不是5和1之后,说B的数字比D的大,可见D的数字只可能是1或2。但究竟是1还是2,不能判定,故不能由此决定D的数字。用两个问号填入表格中,如表5-13-5:
表5-13-5
2.若选②,即B的数字不比D的大。
D的数字只可能是4或者是5,也不能断定究竟是什么数字。也用两个问号填入表中,如表5-13-6:
表5-13-6

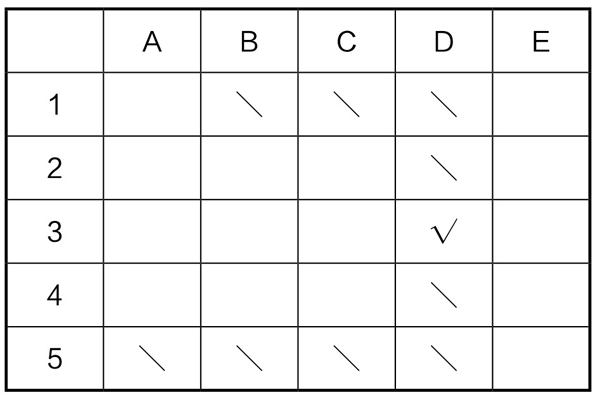
3.若选③,即D不知道B的数字与他的数字哪个大,因此前面两种情况都不可能,所以D的数字不是1、2,也不是4、5。这只有一种情况:D的数字是3。如表5-13-7所填符号,便将D的数字为3确定下来。
表5-13-7
当教师再问B“C的数字比你的大吗?”时,B已经知道C的数字不是1、5, D的数字是3后,得到了否定回答,这说明B的数字比3大,必然是4;于是C的数字必是2,而A只能是1;剩下的5,就只能为E所有。在表上作业(画记号“\”或“√”)的最后结果,如表5-13-8所示。
表6-13-8
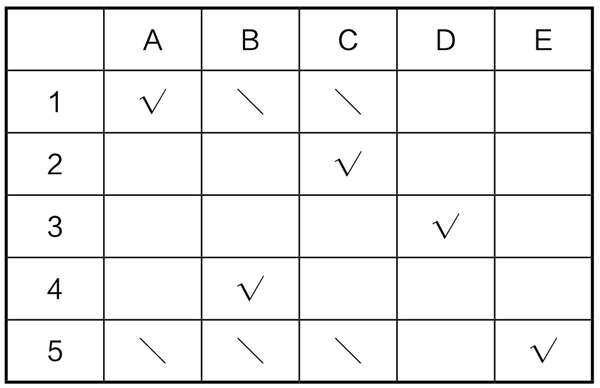
于是小明推断出了所有人卡片上的数字,依次是:A——1, B——4, C——2, D——3, E——5。
读者试想:如果不用列表,只凭推理,事情就会变得很复杂,理不清思绪。列表的目的,就是能够将我们每步推理的结果记录在表里,帮助我们进行下一步的推理。这便使推理容易进行了。
