蝴蝶定理的巧证和引申——蝴蝶定理趣谈
十一、蝴蝶定理的巧证和引申——蝴蝶定理趣谈
1815年,西欧《女士与绅士日记》杂志上刊登一道数学证解题(见书末参考文献[10]P640),引起人们广泛兴趣。题目如下:如图5-11-1,过圆中弦AB中点M任作二弦PQ、RS,设它们分别交圆于P、Q、R、S。连接PS、QR,分别交AB于E、F,证明EM=FM。
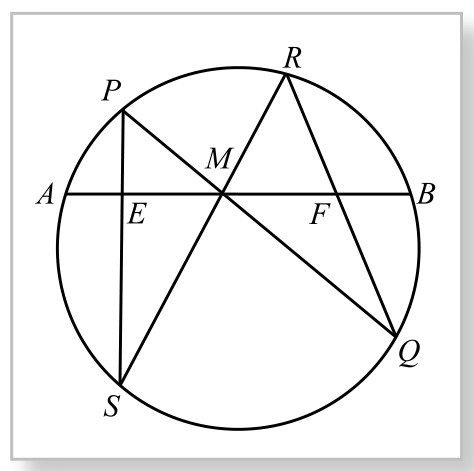
图5-11-1
从图形上看,好像一只飞翔的蝴蝶,所以人们就把它叫作“蝴蝶定理”。
这是一个看似漂亮,却有一定难度的有趣的几何题。
据说第一个证明者,是英国的一个中学数学教师——霍纳(W. G. Horner,1788—1837);他也是欧洲第一个提出多项式数值解法的数学家,他所发明的多项式数值解法,在欧洲被称为“霍纳法则”。该方法早在宋代就已经被中国数学家贾宪首先发现,当时被称为“增乘开方法”。
不过霍纳最初证明蝴蝶定理的方法很烦琐,与该定理的优美形式很不相称,很快就被新的较简洁的证明方法所代替。
自20世纪70年代以后的20年中,我国数学家和数学教师,以及数学爱好者,对该定理很感兴趣,发现了多种有创意的证明方法。这里介绍几种。
[证法一](严济慈证法)
如图5-11-2过S作SS′∥AB,交圆于另一点S′。过M作MT⊥SS′,由圆的对称性得:MS=MS′;∠RSS′=∠MS′S。连接QS′,因Q、R、S、S′共圆,故∠RQS′+∠RSS′=180°。又因为SS′∥AB,∠BMS′=∠MS′S =∠RSS′,所以∠RQS′+∠BMS′=180°,从而Q、F、M、S′共圆。因此∠MS′F=∠MQF=∠PSR,而有△SME≌△S′MF(ASA),得EM=FM。
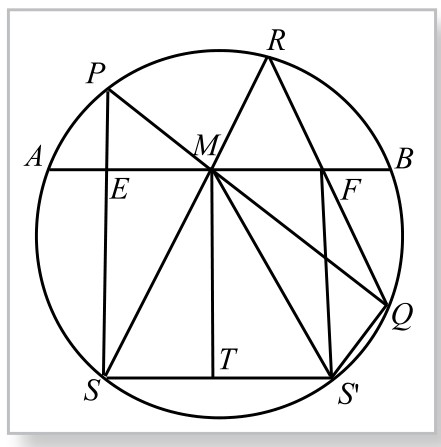
图5-11-2
该证法是严济慈先生青年时期所做,写在了他的著作《几何证题法》(1928年出版)中。
[证法二](张景中三角形面积证法)
如图5-11-3设圆心O,过O作RS和PQ的垂线,垂足分别为D、C。又设∠RMF=∠AMS=α;∠PMA=∠QMB=β,则由
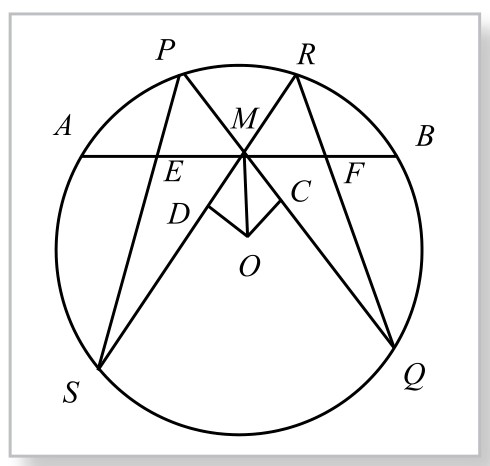
图5-11-3
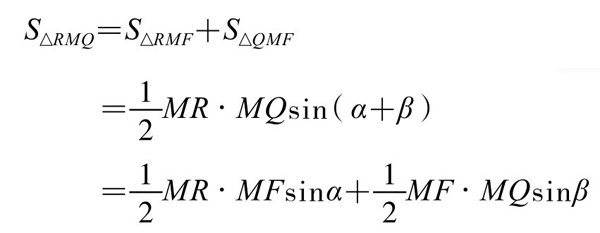
所以有
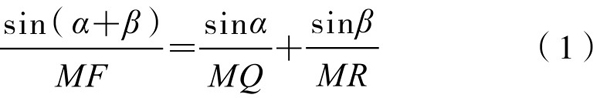
同理有
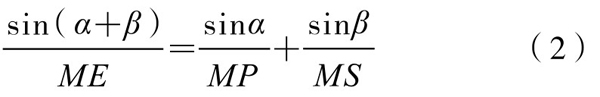
欲证ME=MF,只需证明(1)与(2)式右边相等。而这等价于
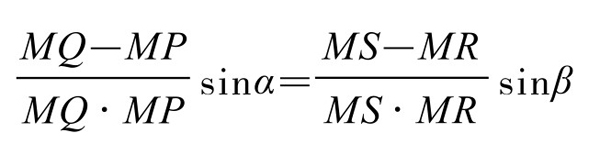
但由相交弦定理知MQ · MP=MS · MR,故只需证明
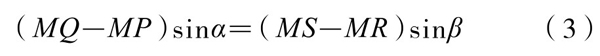
即可。由所作知,MQ-MP=2MC, MS-MR=2MD。
因此,又只需证明MCsin α=MD sin β,即(https://www.daowen.com)
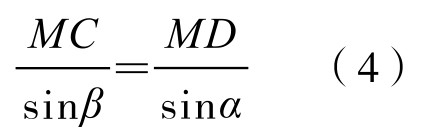
但因∠DMO=90°-∠AMS=90°-α,而又c o s∠DMO=c o s(90°-α)=sin α;同理,有cos∠CMO=sin β。
于是(4)式等价于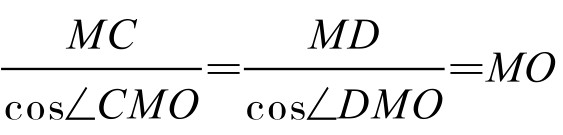
这当然成立。即证。
[证法三](相似三角形法)
如图5-11-4,过圆心O分别作OC、OD垂直PS和RQ,垂足为C、D。由△MPS∽△MRQ,知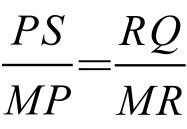 ,从而
,从而
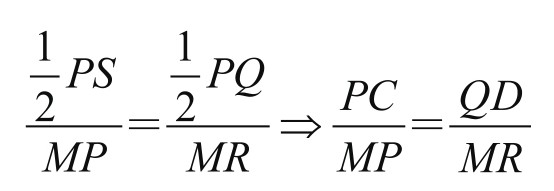
从而有△MCP∽△MDR,得∠MCP=∠MDR。而知∠MCE=∠MDF。但C、O、M、F与D、O、M、E分别共圆,而有∠MOE=∠MCE=∠MDF=∠MOF,即OM平分∠EOF;又因为OM⊥EF,亦即在△OEF中,顶角平分线与底边上的高重合,故知△OEF为等腰三角形。因此底边上的高,也平分底边EF,即ME=MF。原题得证。
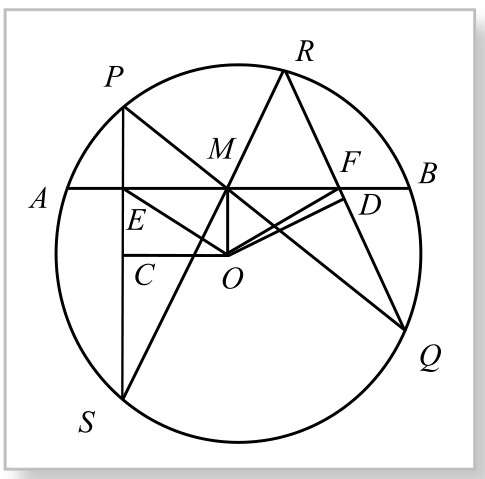
图5-11-4
[证法四](解析法)
如图5-11-5,以M点为原点,以MF为横轴正向,建立直角坐标系。设圆心坐标为O(0,-a),半径r,直线PQ、RS方程分别为y=k1x、y=k2x,则圆的方程为x2+(y+a)2=r2。
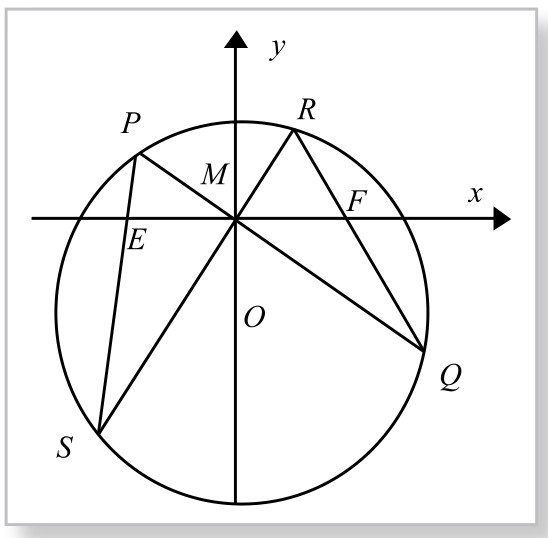
图5-11-5
于是二直线PQ、RS(视为退化二次曲线)与圆组成的曲线系方程x2+(y+a)2-r2+λ(y-k1x)(y-k2x)=0……(*)
就表示过P、Q、R、S四点的二次曲线族。
在(*)中,令y=0,得二次方程
x2(1+λk1k2)+a2-r2=0……(**)
此即为曲线系与Ox轴的(两个)交点坐标应满足的关系。而因该二次方程的一次项系数为0,故知其两个根关于原点对称。而这两个根,恰是E、F两点的横坐标。这正说明E与F的横坐标为相反数,其绝对值相等。亦即ME=MF。原题结论得证。
这个解析证明,充分利用代数与几何的形数巧妙结合,简单明了,的确称得上是奇思妙想。
该定理的奇妙,不仅是它的证法多样化,而且它还有多种奇妙的推广和变化。
推广一,将AB中点M推广到一般位置,看结论有何变化。我们有以下命题:
命题1.(坎迪定理)圆O中,设M为弦AB上的任意一点,过M任作二弦PQ、RS,分别交AB于E、F,则
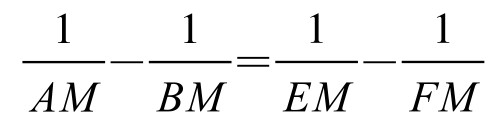
显然,若M为AB中点,那么就是蝴蝶定理。所以这是蝴蝶定理的推广之一。
推广二,将圆推广到二次曲线,得到:
命题2.设AB是某二次曲线(包括椭圆、双曲线和抛物线)的弦,M为AB中点,过M任作二直线,交曲线于PQ、RS,连接PS、QR,分别交AB或其延长线上两点E、F,那么ME=MF。
推广三,我们还可以进一步把二次曲线推广到退化的两条直线——相交或平行的两条直线。得到:
命题3.设l1、l2是两条相交直线或平行直线(图5-11-6、5-11-7)。A、B分别在此二直线上。M为AB的中点。过M任作二直线,分别交l1、l2于P、Q、R、S四点,连接PS、QR,交AB或其延长线于E、F,那么ME=MF。
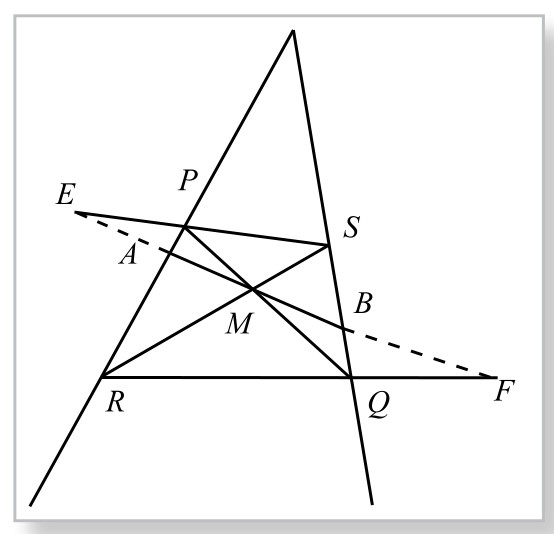
图5-11-6

图5-11-7
推广四,将蝴蝶定理再进行推广,把原题中的圆,推广到特殊四边形——筝形,得到:
命题4.(1990年中国数学奥林匹克选拔赛试题)在筝形ABCD中,M是AC的中点,过M任作二直线PQ、RS,分别交AC于E、F,证明ME=MF。
关于推广的命题3、4,仿照前述证法四的解析证明方法,比较容易。这里就不重复了,留给读者去思考。
你读了以上有关蝴蝶定理的种种巧证和引申推广,是否觉得这只蝴蝶已经飞进了你的心头?
