数学美是学校美育的基础和最重要的部分
三、数学美是学校美育的基础和最重要的部分
(一)数学美有利于文化数学的构建
数学文化化,是数学大众化、数学普及化的重要途径。
数学,是小中大学的必修课程,是人人都要学习的必修课程。数学也是从事任何工作所必须要具有的基本知识。但是,相比于其他课程,特别是相比于文化课程来说,它是难学的课程。特别是中学数学课程改革之后,不少原来是大学才学习的高等数学内容,如解析几何、微积分初步、概率统计初步等,都已经被纳入中学数学教学内容。这使得学生普遍反映数学难学,教师则普遍觉得数学难教。总之中学数学,特别是高中数学,教材水平高过学生接受程度。为此,张应中院士提出“教育数学”的解决方案,他建议把科学数学改造为简单一些、便于进行教学使用的“教育数学”。例如他提出用不等式来代替高中数学里比较难教的极限和微积分,以降低数学内容的难度。
如此虽然能够降低中学数学教学的困难程度,但是,以删除极限和微积分为代价,换取教材难度的降低,似乎得不偿失。因为极限和微积分,是现代数学的思想精华,删去它们,代价太大,而且用不等式来讲解微积分概念,也并不简单。那么,我们能有什么更好的方法呢?有些数学教育界专家学者,提出“数学文化”的概念,即使数学逐步文化化。我们则直接提出“文化数学”的概念,把学校数学改造为“文化数学”,把作为科学的数学课程,改造成文化课程。具体地说,就是大大降低数学的科学水平,而增加数学课程中的文化内涵,把数学史、数学故事、数学与社会、数学与人们生活的联系等文化内容,加入数学教学中去,增加数学课程的文化性。把中学数学改造为文化课程。因为现在的中学教育,已经是全民的教育,而对大多数中学生来说,以后未必需要有很多具体的高等数学知识,他们需要的是数学的思想方法,以及数学实用技术和自学数学的能力。这方面的观点,读者可以进一步参看我们编著出版的《数学文化和文化数学》(书末参考文献[1])。
而数学之美,正是“文化数学”的要素。数学文化,其本质就是要求在数学教材和数学教学中,充分展现数学之美——数学的极简之美、数学的奇异之美、数学的和谐统一之美,以及数学在我们的生活中的种种美妙的应用。
(二)数学美有利于学生的智力开发
所谓创新型教育,培养创新型人才,重在“创新”。而“创新”需要有高超的思维能力、超前的智慧。而数学是思维的科学,数学问题,是催生学生积极思维的有效“激素”。特别是那些有趣的、新奇的数学问题,以及在解决这些数学问题中所表现出来的新奇的、曲径通幽的奇巧方法,使得学生们获得解题后的快乐,是激励学生学习积极性、激发学生智慧的有效途径。
著名数学家陈省身先生在2002年世界数学家大会期间,给中学生题词“数学好玩”。就是因为陈先生在学习和研究数学中,确实得到了数学美的趣味和快乐。
如果说,体育活动是学生的体力游戏的话,那么数学解题,就是青少年的智力游戏。除了以上所说过的数学趣味外,以下还特别强调在民间、在学校里曾经流行过的数学游戏,以及数学智力趣题。
数学趣味性问题或数学游戏,可举出几例作为引子。
1.黄金矩形
定义:宽与长的比是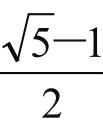 (约为0.618)的矩形叫作黄金矩形。可以通过折纸折叠出一个黄金矩形,详见《数学(八年级下册)》(人民教育出版社2013年9月第1版)第64页。黄金分割点的几何作法,前面已经讲过。现在讲的是黄金矩形,以及黄金矩形中的黄金点。
(约为0.618)的矩形叫作黄金矩形。可以通过折纸折叠出一个黄金矩形,详见《数学(八年级下册)》(人民教育出版社2013年9月第1版)第64页。黄金分割点的几何作法,前面已经讲过。现在讲的是黄金矩形,以及黄金矩形中的黄金点。
如图6-3-1,先作矩形的长边AB,其次作出BA的黄金分割点A1(BA1>AA1),再以BA1为短边长作矩形ABCD(BC=BA1),此即称为黄金矩形。在此矩形中,作正方形A1BCB1;连接A1B1,则AA1B1D仍然是一个黄金矩形,继续在短边AD上作黄金分割点B2,又可以得到下一个黄金矩形AA1A2B2。继续下去,可以不断迭代出一系列黄金矩形。如图6-3-1中所示的AA1B1D、AA1A2B2、A1A2A3B3、A2A3A4B4四个黄金矩形,就是由黄金矩形ABCD迭代4次生成的。
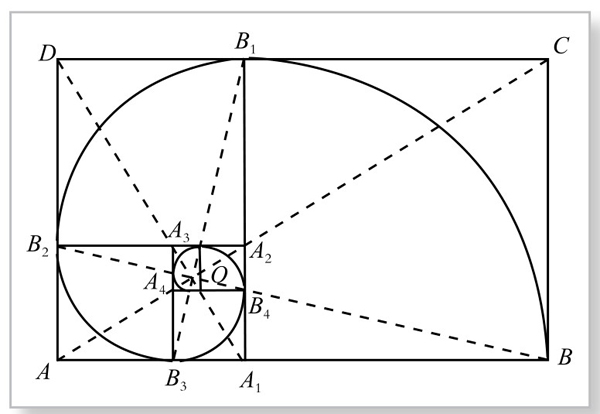
图6-3-1 黄金矩形和黄金点
已探究出黄金矩形至少有以下性质:
性质1.在黄金矩形ABCD内作正方形A1BCB1,则矩形AA1B1D也是黄金矩形。
性质2.所有黄金矩形都相似,且Xn+1与Xn的相似比相同。
点O是黄金矩形ABCD内的一个黄金点,当迭代次数逐步增大时,黄金矩形越来越小,迭代的终点是点O。细心的读者一定会发现,图中的迭代,是使矩形依次按逆时针方向旋转90度。当然,亦可按顺时针方向旋转,如图6-3-2。
在日常生活中,我们经常用手机或相机拍摄各类照片。怎样才能拍出有美感的照片呢?在所用的手机中,执行“设置”→“相机”→“参考线”操作后,再打开“相机”准备拍照时,手机屏幕上就会出现“参考线”。相机中为什么要设置这样的“参考线”?让我们以“数学的眼光”来深究其中的奥秘。
图6-3-2是“蒙娜丽莎”头部的构图,头部整体给人以美感。尤其是“蒙娜丽莎”脸部含有两个黄金点,并且眉心、鼻尖各对应一个黄金点,这就是“蒙娜丽莎”为什么这么美的奥秘。

图6-3-2 油画中的黄金点
在其他欧洲古代建筑和雕塑中,图中的“点睛之笔”,往往是定在黄金矩形的黄金点上。如下面图6-3-3至6-3-6像所示:

图6-3-3 帕特农神庙(左下螺旋)

图6-3-4 自由女神像(左下螺旋)

图6-3-5 最后的晚餐(左下螺旋)

图6-3-6 掷铁饼者(右下螺旋)
2.七巧板
七巧板(图6-3-7),是我国民间一种儿童智力玩具,它将一个正方形分割成七个不同的基本几何图形——两个大直角三角形、一个中直角三角形、两个小直角三角形、一个平行四边形、一个正方形。然后用这七块基本图形拼成各种各样的图形。如下图人物(仕女)、飞鸟、家禽、建筑、桥梁等图形(图6-3-8至6-3-12)。
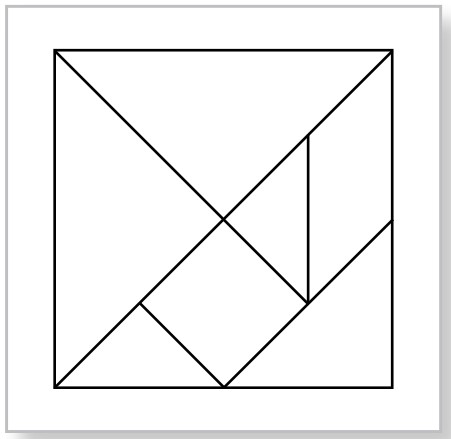
图6-3-7 七巧板

图6-3-8 人物(仕女)

图6-3-9 飞鸟

图6-3-10 家禽

图6-3-11 建筑物

图6-3-12 桥梁

图6-3-13 凸多边形

图6-3-14 任意多边形

图6-3-15 有缺(洞)多边形
我们还可以进一步提出如下数学问题:
(1)用七巧板可以拼成多少种不同的凸多边形?
所谓凸多边形,是指多边形整个图形都在每边所在直线的一侧。例如,开始的那个正方形(图6-3-7)便是一个凸多边形,图6-3-13中每个图形都是凸多边形,而图6-3-14中大部分图形则不是。那么,用七巧板能够拼成多少个凸多边形呢?这是一个并不容易解答的数学问题,但中学生是能够去试着进行研究的。
(2)用七巧板能够拼成多少个有缺口的凸多边形?
所谓有缺口的凸多边形,是指形如图6-3-15中的第一排第二个,第二、三、五排的第一、四个,第六排的第一、三、四个,以及第七排的第二、三个。我们的问题是:像这样有一个缺口的凸多边形,究竟能拼出多少个?
(3)有洞凸多边形问题。
如图6-3-15中第一排第一、三个图形,其外形虽然是凸多边形,但是其中有一个“洞”(而非缺口),即称为有洞凸多边形。我们的问题是:用七巧板能够拼成多少个有一个洞的凸多边形?有两个“洞”的凸多边形能够拼出来吗?有多少个有两个,以至三个、四个“洞”的凸多边形呢?至多能够拼成有几个“洞”的凸多边形呢?
以上关于有“洞”的凸多边形的数目,是一个有趣的数学问题,也可以说是一个数学系列智力趣题。有兴趣的中学生,以至读者,都可以在七巧板的拼接游戏中,探索其中奥妙。
3.图形覆盖与划分问题
图形覆盖与划分,是组合数学中一类常见的问题,而且十分巧妙和有趣味。
问题1.用7块1×2的砖块,能否覆盖有14块方块的缺角园地?用如图6-3-16所示的7块1×2的地砖(面积为2),能否铺满如图6-3-17所示的缺角园地(面积为14)?
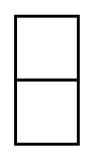
图6-3-16

图6-3-17
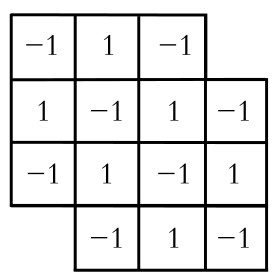
图6-3-18
如果用实际试验的方法来解,是行不通的。因为用7块1×2的地砖来铺地,有多得难以计数的不同类型,试验是难以一一穷尽的。我们应该设计出一种易于判别的形式,来帮助我们进行分析和思考。
设计:将场地中每个格子,相间标上数字“1”和“-1”,使其变成图6-3-18的数字图。现将一块1×2的地砖放到场地上去盖住两格,这两格必然相邻,即盖住的两格中的数字必为1和-1,其代数和为0。
用反证法:假设用7块1×2的地砖盖住了这个园地,那么,其中每块地砖所盖的两个数字的代数和皆为0,因此园地上所有被盖住的数字的代数和应为0。但是,实际上这块园地上有6个“1”,8个“-1”,其代数和等于-2,不为0。这就是矛盾。所以假设不能成立,即用7块1×2的地砖不能盖住这个园地。(https://www.daowen.com)
我们还可以用染色的办法:将场地的小方格相间染成白色和黑色,每一块1×2的地砖,都必然盖住一白一黑两个相邻的小方格。假如能用7块1×2的地砖盖住园地,那么必将盖住7块白格、7块黑格。但该园地上白格与黑格的数目不等,矛盾,因此推出否定的结论。
这种标数字或染色的方法,在处理某些类似的问题时经常有效。
问题2.一块如图6-3-19所示的5×4的园地,另有如图6-3-20所示的5种规格的地砖各一块,它们合起来的面积正好与园地面积相等。问:①能否用这5块不同形状的地砖,将此园地铺满?为什么?②如果限定只用5块某一种规格地砖来铺,哪种形状的地砖可以铺满?哪种不能?为什么?

图6-3-19
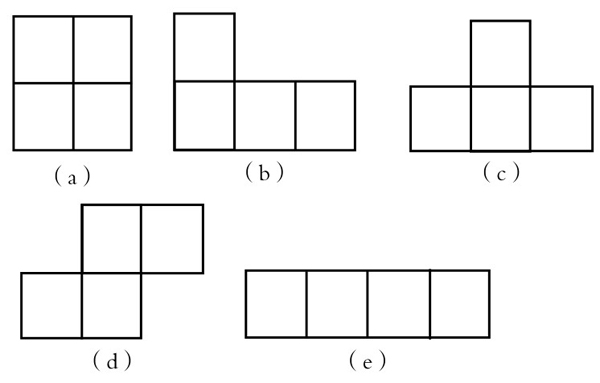
图6-3-20
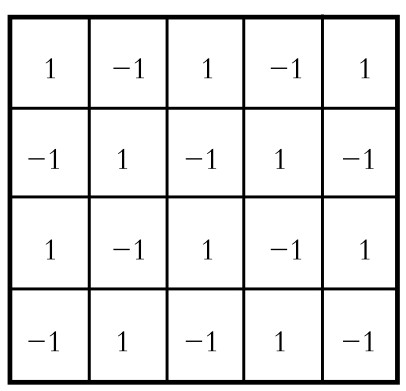
图6-3-21
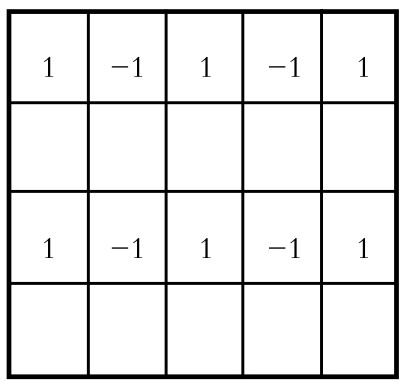
图6-3-22
图6-3-23
解:①如图6-3-21所示,在图6-3-19所示的方格中依次相间填上数字1和-1。由于小方格为20个,其中10个“1”,10个“-1”,故全图上所有数字之和为0。
在图6-3-20所示的5种规格的地砖中,(a)、(b)、(d)、(e)这4种规格地砖中的每一块,不论盖住园地中的哪四格,其盖住的数字皆为两个1,两个-1,其所盖数字之和皆为0。
而(c)规格地砖,不论盖在园地何处,其盖住的数字,不是含三个1和一个-1,就是含三个-1和一个1,其代数和不是2,就是-2,而不可能是0。因此,如果用这五块地砖,不重复地去盖园地的话,那么,它们所盖住的所有数字之和,不是2,就是-2,而非0。这就与园地所有数字和为0矛盾。所以,不可能用这5种规格地砖各一块将整个园地盖住。
②用(e)规格地砖5块,就能够盖住整个园地。而用其他四种规格每种5块都不能盖住园地。为什么呢?
对于(c)规格地砖,不论盖在何处,所盖住的四个数字之和是2或者-2,故5块总和不可能是0。
对于(b),则需要重新设计:将图6-3-21中第2、4行数字擦去,变成图6-3-22所示的情形,于是每块(b)规格地砖,盖住的四个数字之和总是-1或者1,故5块所盖数字之和不可能是0。
对于(a)、(d),再将设计改为图6-3-23所示的情形,则每块(a)规格地砖只能盖住一个数字,5块只能盖住5个数字,而图6-3-23中有6个数字,因此不能盖住整个园地。同样,每块(d)规格地砖也只能盖住一个数字,故也排除。
(三)数学美有利于培养创新意识
创新意识,是创新型教育的前提。没有创新意识,就根本谈不上创新型人才的培养和教育。而审美意识,是创新意识的出发点和激发器。只有在美的环境下,只有欣赏到美好的事物,才能够产生对美好事物的向往和追求,才能够从事创造性劳动,创造出新型、美好的作品和产品,成为创新型人才。
而数学美,则时刻体现在我们生活的环境之中,反映在学校的各个课程的内容之中。只要我们留心,就能够发现数学之美。如果扩大我们的视野,将目光投向室外,投向广阔的空间,那么,我们处处都能够体验到数学之大美。
其实,世界处处是数学的课堂,自然界就是几何图形的天地。我们走在城市的大街上,那些高楼大厦、天桥立交都体现出几何图形之美、数学变化之美、数学奇异之美。
例如,我们带读者到我国改革开放的最前沿——深圳经济特区去实际走一走,看一看吧。那里有高耸入云的楼宇和宽阔的高速公路,以及各式建筑,无不令人心醉。
首先,我们来到深圳湾公园,满眼的“几何美”震撼了纸上谈兵的“几何人”。请看,原来工程师和工人们,早已把纸上的数学之美、几何图形之美,变成了现实之美。
非欧几何大师黎曼、罗巴切夫斯基认为平行线不一定不相交。果然我们在公园看到的平行线未必是真平行线,看到的不平行的线未必不是平行线。就像我们看到的椭圆可能是圆,看到的圆又可能是椭圆,这就是仿射几何学的体现。
奇妙的空间几何,不只是数学课本里的知识,更是现实中美的化身。
几何不仅仅是科学,也是哲学:虚与实、繁与简、曲与直、大与小、方与圆、黑与白……虽然它们的形态不相同,但是完全可以相融。

图6-3-24 建筑室内顶棚设计

图6-3-25 体育馆穹顶
我们走在深圳的大街上,徜徉在公园里,会发现,数学如诗一样存在。诗曰:
惊喜之中,似曾相识,实不相识。
这壮丽的建筑似惊人的巨浪。
乱石穿空,惊涛拍岸,
卷起千堆雪。
江山如画,一时多少豪杰。
遥想公瑾当年,小乔初嫁了,雄姿英发。

图6-3-26 建筑室内装饰1

图6-3-27 建筑室内装饰2
建筑设计师高迪曾经说过:直线属于人类,而曲线属于上帝。曲线、直线相伴构成丰富多彩的美丽图案。惊喜之中,似曾相识,实不相识。
曲线包围着直线,直线衬托着曲线,构成了一幅幅美丽如画的建筑图形。惊喜之中,似曾相识,又不识君。
因为人们喜欢直线,简单、直来直去。偏偏大自然却是以各种曲线存在的,科学家为了满足人们的视觉需要,经常用直线做出精美如画的曲面来!你看看这幅曲面图(图6-3-28)就是由直线构成的,多么美妙!
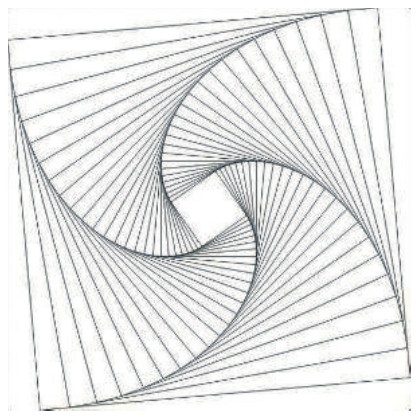
图6-3-28 直线组成的曲面形

图6-3-29 由线条表现出来的立体图形
图6-3-29的立体图形,是由一个双曲线围绕它的虚轴旋转360度而成的“直纹面”,也是各种各样的二次曲线(圆、椭圆、抛物线、双曲线)的集合。而图6-3-30让人意识不到它是单纯由无数直线旋转而成的,这就是它奇妙的地方,也是魅力所在!
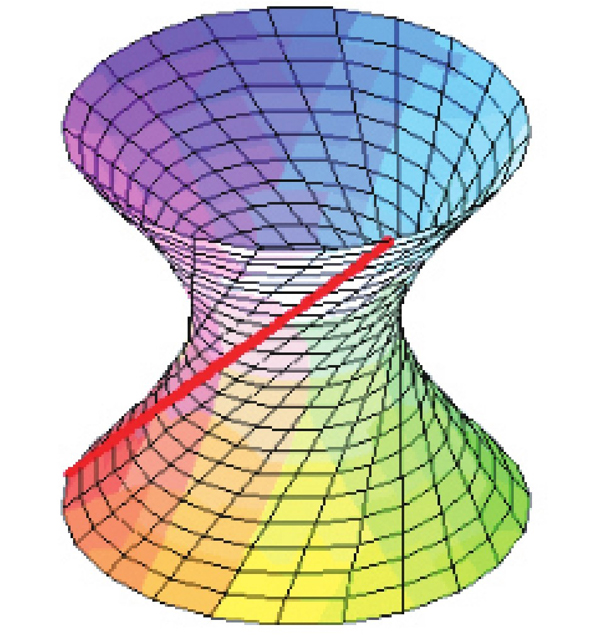
图6-3-30
如果把图6-3-30的直纹面向纵向拉伸,就成了广州塔——“小蛮腰”(图6-3-31)!

图6-3-31 广州塔“小蛮腰”
再从网络上搜一搜,看看深圳平安大厦(图6-3-32)、北京大剧院(图6-3-33)和上海浦东新区建筑群(图6-3-34)吧,各种高楼大厦各具个性,但是都充分显示了几何图形之美,“数学之美”。

图6-3-32 深圳平安大厦,荣膺亚洲顶尖建筑设计奖

图6-3-33 北京国家大剧院

图6-3-34 上海浦东新区,高耸着的东方明珠塔特别显眼
再看看中国人引以为傲的高铁和高速公路网,以及大江大河上横空出世的大桥吧,犹如一条条“天路”穿山越岭,横跨在高山峡谷之间,令世人惊叹!但它们的建设,首先就需要数学计算,是数学、力学和美的结合。如果你想要加入到建设者的队伍里,成为它们的设计者和建设者,那么首先学会数学和相关科学技术,领会数学之美带给你的智慧和灵感吧!
在大桥建设数量上,我国是世界上当之无愧的第一。仅在万里长江上,截至2016年,在建和已建成的桥梁就有87座,而重庆市以32座在桥梁总数中排第一。其次是湖北25座,江苏、上海13座,四川6座,安徽8座,江西3座。其中,重庆市仅在市区就有跨江大桥11座,(图6-3-35)就是其中之一,公交轻轨两用。

图6-3-35 朝天门长江大桥为目前世界第一大跨径拱桥
重庆朝天门长江大桥仅有两座主墩,主跨达552米,比世界著名拱桥——澳大利亚悉尼大桥的主跨还要长。
如果,我们把学校的课堂,搬到大自然中,把书本里的数学知识,联系自然界和社会上的具体形象,就可以切实感受到几何图形的优美。因为无论是什么建筑、桥梁或高速路网,都是科学技术和力量的完美结合,而其核心技术,则是计算和设计,其理论核心都是数学与数学技术,都是数学美的外在表现。
正如著名数学家华罗庚所说:大哉,数学之为用!妙哉,数学之为美!
