从兔子繁殖引出的优选数列
三、从兔子繁殖引出的优选数列
关于上一篇中所述的“先输组”序列,以及用无理式表达正整数的函数式,还有其更有趣的历史源头,以及更广泛的与现实应用的联系。
(一)历史源头
欧洲中世纪,史称“黑暗的中世纪”,宗教统治压制和扼杀了科学思想。整个中世纪,欧洲的数学几乎没有什么进步,远远落后于东方的中国和阿拉伯等地区。只有一个人值得提及,那就是意大利的斐波那契(1175—1250),在黑暗的中世纪,他像一盏明灯,给欧洲数学带来了一缕微光。他的最大贡献是,在青年时期游历北非和阿拉伯半岛之后,把先进的阿拉伯数学,特别是关于“印度-阿拉伯数码”及其计算方法,带回了欧洲,并写出了数学著作《计算之书》(1202年),成为欧洲人此后学习数学通用的“百科全书”,被广泛使用了200年之久。

图5-3-1 斐波那契
就在他这本书中,还载有一个影响广泛而又饶有趣味的数学问题——兔子繁殖问题。问题所述如下:
如果每一对大兔,每月可以生一对小兔;而每对小兔两个月后即成为大兔。那么由养一对小兔开始,一年后可以生出多少对兔子?
问题的解决并不困难。可列表5-3-1计算如下:
表5-3-1

从中可以发现一条规律:表的下列,即兔子对数,从第三项开始,每个数都是前面两个数字之和。若设数列的通项为Fn,则数列{Fn}有以下性质:
(1)F1=F2=1;
(2)Fn+1=Fn-1+Fn, n≥3;
而且特别奇怪的是,该数列的通项公式,竟然可以用无理式来表示:
(3)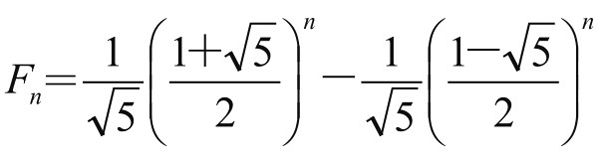 ,n=1, 2, 3, …
,n=1, 2, 3, …
正因为这个数列有很不平凡的特点,引起人们广泛而长久的兴趣。人们把该数列用发现者本人的名字来命名,称为“斐波那契数列”(或简称F-数列),并不断发现它的许多奇妙性质,以及在优选法等多个方面的重要应用价值。
(二)奇妙性质
F-数列的性质有许多,并不断有新的发现。1963年起,美国创办了一份数学趣味杂志《斐波那契数列季刊》,专门发表关于“F-数列”的论文和故事。以下列举几个常用性质:
(1)Fn2-Fn+1Fn-1=(-1)n-1。
(2)F1+F2+F3+…+Fn=Fn+2-1。
(3)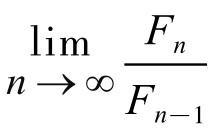 0.6180339887…=ω 。
0.6180339887…=ω 。
即F-数列后项与前项之比的分数序列有极限,其极限值就是黄金数ω:
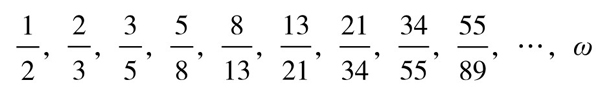
因为由Fn+1=Fn-1+Fn,两边同被Fn除,得
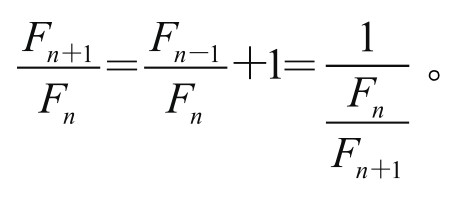
设数列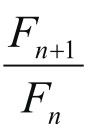 的极限为y,在上式中两边取极限,便得
的极限为y,在上式中两边取极限,便得
y2+y-1=0或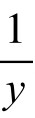 =y+1 y2+y=1。(https://www.daowen.com)
=y+1 y2+y=1。(https://www.daowen.com)
二次方程求解得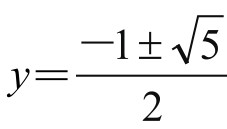 ,取正值,得
,取正值,得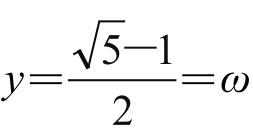 ,此即黄金数。
,此即黄金数。
(4)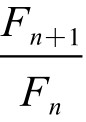 →f=1.6180339887…=1+ω。
→f=1.6180339887…=1+ω。
(5)已如前述,ω还可以表示为连分数:
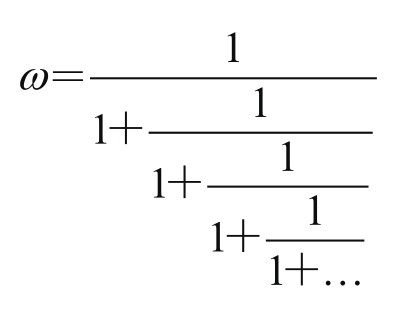
(三)两个相关的特殊函数
已如前述,特殊函数f(n)=[na], g(n)=[nb],其中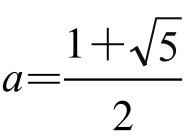 ,
,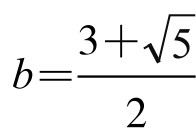 ,曾经出现在第20届国际数学奥林匹克竞赛题之中,而且引起过不小的轰动。因为这两个函数形式十分古怪,又有奇怪的性质。
,曾经出现在第20届国际数学奥林匹克竞赛题之中,而且引起过不小的轰动。因为这两个函数形式十分古怪,又有奇怪的性质。
性质1,两个函数都是递增数列;两个函数的值域F=f(Z+)、G=g(Z+)不重不漏,完全覆盖了整个正整数集合,即
f(Z+)∪g(Z+)=Z+;F(Z+)∩G(Z+)=Ø。
性质2,函数f(n)有递归表达式:
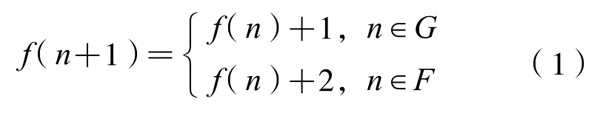
关于它的证明,上节已经说过,这里从略。根据(1)式,可以从f(1)=1开始造出f(n)的函数表,并由此得到g(n)的函数值。
性质3,
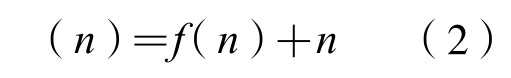
由此得以下推论:
1≤f(n+1)-f(n)≤2
2≤g(n+1)-g(n)≤3
f(f(n))=f(n)+g(n)
可以较快地求得f(240)=388。
性质4,
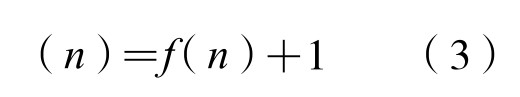
性质5,
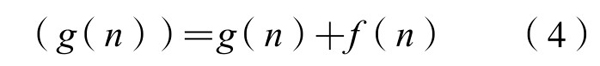
即:函数g(n)在|1, f(g(n))|上的取值个数与在片段|1, g(f(n))|上的取值个数一样多,即f(n)个。
由此可见,数学中有些初看起来不相关的概念、问题或函数可能有着内在的联系。善于发现这些内在的联系,可以激发我们的数学智慧。
(四)优选序列
“斐波那契数列”又叫作优选序列。这是什么原因呢?我们在“(二)奇妙性质”(3)中说道:“F-数列”前后项比的分数序列的极限为黄金数ω≈0.618时就体现了这一点。
优选法,即所谓“0.618”法,就是说在优选区间中第一个实验点,应选在区间的0.618处,这样可以用最少的试验次数,获得较优的试验效果。但是要计算出一个具体的试验区间的0.618点,比较复杂。
所以在优选法的实际应用中,不是计算0.618点,而是用的近似分数序列: ,
,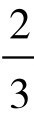 ,
, ,
,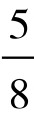 ,
,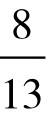 ,
,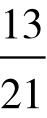 ,
,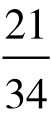 ,
,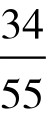 ,
,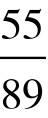 ,…中的某个分数来代替0.618。例如将实验区间分成13等份,第一、二个实验点即选在第5、第8两点。5和8正是(不大于21的)两个F-数列数字。而且这两个点关于区间的中点是对称的。此即华罗庚先生所说的“对称折纸”的理论根据。
,…中的某个分数来代替0.618。例如将实验区间分成13等份,第一、二个实验点即选在第5、第8两点。5和8正是(不大于21的)两个F-数列数字。而且这两个点关于区间的中点是对称的。此即华罗庚先生所说的“对称折纸”的理论根据。

如果实验的区间较大,可以将区间等分成34份,第一、二个实验点选在13和21(关于区间的中点也对称)点上。若21点比13点效果好,便舍弃区间[21, 34],在剩下的区间[1, 21]上再对称选点8,13(也是对称选点)来作实验。如此等等。直到最后选出最优点为止。
将区间等分,对折区间(纸条),对称取点,这比计算0.618简单得多。
所以将斐波那契数列,称为“优选序列”是适合的。这也是“斐波那契数列”在实际应用中的重要价值。
斐波那契数列的“优选”性,还可以在自然界中体现。例如,花瓣的数目,往往符合“斐波那契数列”中的数字,如三瓣、五瓣、八瓣等等;葵花花盘的螺旋状条纹路排列数,也是服从“斐波那契数列”的数字;树枝分叉数目,往往也是按照优选序列数目生长出来的。
