易拉罐中有数学

九、易拉罐中有数学

问题：现在到处可见的易拉罐（图5-9-1），为何大多设计成圆柱状，其长度和圆柱直径之比多大为好？

分析：易拉罐外形设计的合理性，与预定的优化标准有关。其一，在同样体积的要求下，以使用的包装材料是否节省来判断优劣；其二，以焊缝的长短为标准来判定优劣。现分别对两种情况进行讨论。

1．节省包装材料。

在体积V为定值的条件下，求圆柱体的表面积S最小值。

设圆柱体的高为h，底面半径为r。由V=πr2h，得。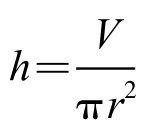

又因为

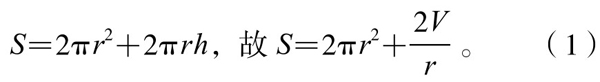
由均值不等式知：

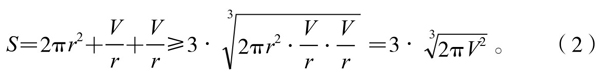
其中等号当且仅当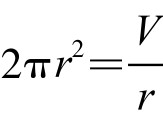，即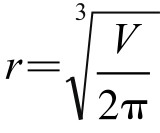时取得。此时h=2r，表面积S有最小值min{S}=。

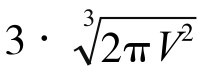即当圆柱体的高与底面直径相等时，表面积有最小值。

至于（1）式中右边的两项，为什么要在（2）式中分成三项，是因为要使这几项之积为常数，才能运用极值定理。

2．考虑缩短焊缝。

事实上，大多数易拉罐的外形不是等边圆柱体。为什么呢？这可能有两个原因：第一，易拉罐的底面与侧面所用的材料厚度不同，因此价格不同；第二，为使焊缝缩短。

先考虑第一个原因：

设底面材料单位面积价格，与侧面材料单位面积价格分别为λ1, λ2（λ1≠λ2），则做一个易拉罐的价格为

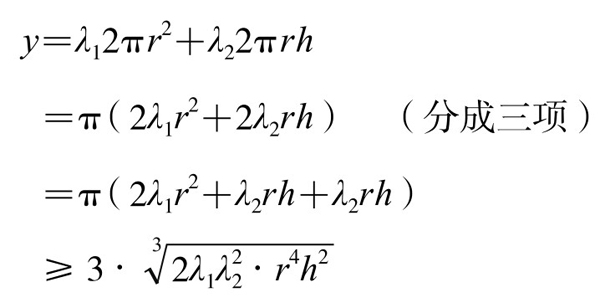
当且仅当2λ1r2=λ2rh，即h=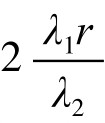时，等号成立。此时y取最小值，但是易拉罐的外观，已经不是等边圆柱了。

再考虑第二个原因：

易拉罐焊缝，由上下两个圆和侧面一条直线构成，其长度为

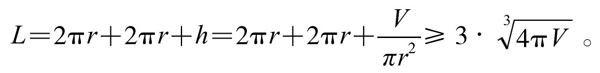
当且仅当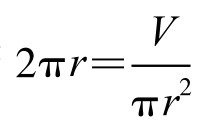，即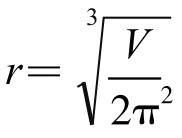时，取等号。此时L取最小值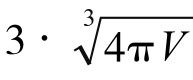，而易拉罐的高h=2πr，即它的高等于底面圆周长。这时易拉罐外形就成了长条形的圆柱形了。

可见以不同的标准，就会有不同的最佳设计方案。