电梯升降停靠站设计有学问
十、电梯升降停靠站设计有学问
(一)一个现实问题
一栋33层的大楼有一部大型电梯,停在第1层。从乘客满意的程度考虑,每次上升时,在第2至33层之间停几次、在哪几层停最合理?
分析情况,明确问题:
所谓“满意程度”没有数量意义。所以,首先要把“乘客满意程度”数量化。
一方面,对于已经登上电梯的乘客来说,如果电梯不能停到他所需要去的楼层,还要他走上,或走下一层或几层,那么,他就感到不满意,而上楼又比下楼更让人不满意。因此对于这些已经上了电梯的人来说,希望多停几次,每层都停,就可以把所有人送到位。
另一方面,对于在下面等电梯上楼的人来说,希望等的时间越少越好,因此,希望已经开动的电梯在运行中少停几次。
那么,怎么才能平衡人们的满意度呢?
(二)数量化和合理简化
为了便于计量研究,我们设法将以上“不满意”程度数量化:假设步行下楼一层,不满意程度为1分/人;步行上楼一层,不满意程度为3分/人;电梯停一次,在下面等电梯的人,感到不满意程度为5分/次。
这样就使上下楼的人的“不满意”程度数量化了。
因为上楼到各层的人是随机的,可以作如下假设,将问题进行合理简化:
首先,假设到每层都有1人,而先不考虑下面等电梯的人。现有32人在第1层,他们分别要去第2至33层的某一层,而电梯在中间只停一次,那么停在哪一层,这32个人的不满意分数总和最小?
其次,考虑在下面等电梯人的不满意程度,电梯在一次运行中停几次,使所有人不满意程度最小?
(三)建立数学模型
1.设电梯停在第x层。在第一层有y人没有乘电梯而直接走上楼,32-y人乘电梯上楼。显然,这步行的y人,是住在较低的第2~(y+1)层的某一层,其余的人则分别住在第(y+2)~33层的某一层。现在来计算这32人不满意的总分S。
由于要使不满意总分最小,自然要求y<x。下面分两部分来计算:
第一部分——步行上楼的y人不满意分数。我们先来计算他们总共步行了多少层楼:第一人从第1层楼梯走到第2层,第二人从第1层楼梯走到第3层,……,第y人从第1层楼梯走到第y+1层楼,上楼梯的总层数为1+2+…+y=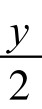 (y+1),故不满意总分是:
(y+1),故不满意总分是: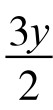 (y+1)。
(y+1)。
第二部分——乘电梯上楼的人不满意分数。这32-y人中只有住第x层的那位满意;除此以外,其余人都要往上走或往下走,都感到不满意:
第x+1层到33层的住客,要分别往上走1~(33-x)层,因此,不满意的总分数是:3×[1+2+…+(33-x)]=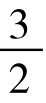 (34-x)(33-x);(https://www.daowen.com)
(34-x)(33-x);(https://www.daowen.com)
第y+2层到x-1层的住客,要分别往下走1~(x-y-2)层,因此,不满意的总分数是:1+2+…+(x-y-2)=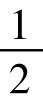 (x-y-1)(x-y-2)。
(x-y-1)(x-y-2)。
总计以上三项,总和为:
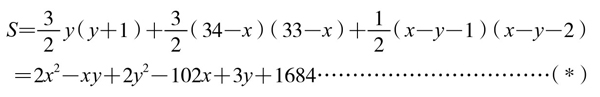
于是,我们的问题就变为一个数学问题:求二元二次函数(*)的最小值。
将(*)式右边进行两次配方,得
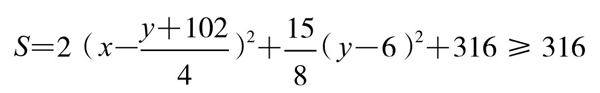
显然,当x=27, y=6时,S=316是最小值。这就是说:当电梯停在第27层,下面有6人步行上楼时,所有人的不满意总分最小,总分为316分。
2.若电梯只停一次,如上面已经算过,不满意总分最小为316分,加上下面等的人不满意5分/次,不满意总分为316+5×1=321分。
如果电梯每一层都停,即停了32次,上下楼的所有人都满意,而在下面等的人不满意总分有5×32=160分。显然不满意程度低于前者。
3.改进停靠方式。
能否改进电梯停靠方式,使不满意总分更小?
如果电梯连续三层都停,那么中间一层可以不停。因为这样做,减少了一次下面等候的人不满意的5分;而中间层的人往下走一层,只增加1分不满意。合起来减少了4分不满意。
如果电梯连续停三次,每次间隔1层,设为第m-2、m、m+2层,那么第m-1、m+1层的人各向下走一层,不满意各1分,下面等的人不满意5×3=15分,共2+15=17分;如果再去掉中间一次,则m-1层向下走一层,不满意1分,m层的人向下走两层,不满意2分,m+1层向上走一层,不满意3分。但减少了一次下面等的人的不满意5分,总共1+2+3+5×2=16分。所以这中间一次也可以不停。
如果电梯连续停三次,每次间隔2层,设为第m-3、m、m+3层,易算得不满意分数为21分;若去掉中间一次,则不满意分数为23分。可见,这时中间一层不能去掉。
因此,以每隔2层停一次,最为可取。
如果每两次停之间隔3层,怎么样呢?间隔3层,不如间隔2层效果好。理由如下:在12层之间,每隔2层电梯停1次,只可以停3次,不满意分数为27分;若间隔3层电梯停1次,只可以停2次,不满意分数为28分。可见,电梯每隔2层停一次的不满意分数较小。
于是我们可以设计间隔2层电梯停机一次的方案(三种)如下:
(1)2, 5,8,11,14,17, 20, 23, 26, 29, 32;
(2)3, 6, 9,12,15,18, 21, 24, 27, 30, 33;
(3)4, 7,10,13,16,19, 22, 25, 28, 31, 33。
方案(1)不满意总分为88分;方案(2)(3)不满意总分都是86分。相比之下,方案(2)(3)为佳,它们比每层都停,或只停一次的方案要好。
