一、万物皆数
(一)人类对世界本源认识的追求
古代人自有思维能力之后,面对天地万物,大多数人茫茫然、昏昏然。
但其中的智者、哲人,却不满足自然的支配和赐予,思考和追寻着万物的本源为何的问题。东方的中国华夏先民,曾经认为万物的本源是“五行”,即金、木、水、火、土这五种基本元素;而西方先民则有以火为尊的拜火教,有崇拜太阳神的古希腊民众。毕达哥拉斯及其学派则以数为宗,认为“万物皆数”。

图3-1-1 毕达哥拉斯
毕达哥拉斯(前580至前570之间—约前500)是古希腊伟大的数学家和哲学家。他出生在爱琴海东岸小亚细亚沿海的萨摩斯岛上。年轻时他到埃及、巴比伦等地游学,40岁后回到故乡,不久迁到意大利南端的克罗托内,创立一个有宗教色彩的政治、学术团体,并以他的名字命名。后人称之为毕达哥拉斯学派。这一学派把“万物皆数”作为信条。他们认为:一切事物都是由其本原构成的,从它派生出来的,最后又复归于它。这个本原就是“数”。
例如,有五个人,尽管他们各不相同,性格各异,寿命长短不一,即使其中有人死了,或者若干年后都死了,但是曾经有过五个人的事实,却是永远存在的。物去而数自在。所以说,这个数“5”就是这五个人的本原。
毕氏为什么会有如此的认识呢?他认为万物的形态都在变化,其中不变的只有它的“数”。所以“数”是万物的本原所在,是万物存在的元素。万物皆是“数”的反映,是数的不同的表现形式。简而言之,就是“万物皆数”。他把这一口号,作为该学派不可动摇的信条。这其中所说的“数”,当时只限于有理数,而且是正数,即是正整数和正分数。
同属于毕氏学派的著名人物菲洛劳斯所说的如下一段话,可以让我们更好地理解这种思想。他说:任何一种东西之所以能够被认识,是因为其中包含一种数;没有这种数,心灵不能思考,也不能认识任何东西。
不过,那时毕氏及其学派,是从几何的角度,来认识和说明数的,即寓数于形之中,把数附属于几何图形。把单个的数(正有理数)称作“线段数”,两个数的乘积称为“面积数”,三个数的乘积呢,则称为“立体数”。而四个数或四个以上数相乘,则不被允许,因为没有相应的几何意义。
数是怎么得到的呢?对于“可数”的离散物体,如手指、石子、野兽等,可以用数(数数)得到。若连续量,没法数,可以用一个单位量作为标准,来度量出它的数量。对于线段,则可以用一个单位长的线段作为标准,来度量它的长短。如果能量尽,即得(正)整数;如果量不尽,便用剩余的零头,来量第二条线段(即单位线段);若再量不尽,再用第二次剩余来量第一次的剩余线段。如此辗转相量(辗转相除)。他们认为:最后总能有除尽的时候,从而得到原来两条线段的最小公共除尽的线段(最大公约线段)。于是,原来两条线段都是这个公约线段的倍数。所以,在毕达哥拉斯眼里,任意两条线段都有公共最大公约量(基本单位线段)。所以,“线段数”只有(正)整数和分数。那时没有负数的概念。
由此看来,毕达哥拉斯是原子论者。即他们不认为线段是无限可分的,线段有最小的单位,最小组成部分,把它称为“原子”。因此,任何两条有限长度的线段,辗转相除,都是可以互相“量尽的”(可公度的);不存在两条不可公度的线段。
后来该学派中有个成员叫希帕苏斯的,他发现正方形的对角线与其边不可公度(已如前述)。
因为每一次公度,都只能产生一个有理数。现在发现有不可公度的两条线段,亦即发现了一种新数——竟然不是正有理数(现在称为无理数)。
今天看来,毕达哥拉斯的这种“万物皆数”的哲学观,并不合乎科学。数是物的抽象存在,怎么能说是万物的构成的本原呢?但是这种哲学观,却大大提高了人们对“数”和数学的关注和研究兴趣,使得演绎数学得以诞生,使数学成为开启所有科学的金钥匙和奠基石。这又功莫大焉!
(二)东方哲学家的呼应
世界人类的历史,往往有一种神奇的同步现象:在远隔万里的东西方不同地域的人们,在没有任何交往和联系的情况下,竟然能够有完全相同,或大体相同的想法和思维方式。作为对毕达哥拉斯“万物皆数”观点的呼应,在东方的中国,在大致相同的年代里,居然有十分相似的观点和论断。老子(约前571—前471)是中国第一位伟大的思想家和哲学家,他与毕达哥拉斯处于同一时代,两人可以说是绝对没有任何联系的可能性。但是,奇怪的是他俩似乎心有灵犀一点通,都对数情有独钟,都对数有强烈的崇拜。

图3-1-2 老子和《道德经》
老子生活在我国的春秋晚期,比孔子约年长20岁,姓李名耳,字聃,“老子”是后人对他的尊称。孔子曾经问学于老子。老子的整个哲学体系的核心范畴是“道”,提出了天道无为的思想,反对天道有知的宇宙观。在老子以前和老子的时代,人们认为天是有意志的,是最高的神,可以主宰万物,人世间的一切都是由它决定的。老子经过考察、了解自然界的变化,认为天只不过是一种物质,它没有意志,不能主宰人世间的吉凶祸福,“道”才是天地万物的本源。那么,“道”是什么呢?他解释说:“有物混成,先天地生。寂兮寥兮,独立而不改,周行而不殆,可以为天下母。吾不知其名,字之曰道。”意思是说,有一个浑然一体的物质,在天地出现之前就已有了。它看不见,听不到,摸不着,独立地存在,按照一定的规律循环运行着。它产生万物,它是宇宙万物之母,我不知道如何称呼它,就给它起个名字叫“道”。
“道”在老子的心目中是无形、无象、无体的,是世界万物的本源。那么,“道”是怎样演化出万物的呢?他说:“道生一,一生二,二生三,三生万物。”他又强调说:“人法地,地法天,天法道,道法自然。”即人以地为根据,地以天为根据,天以道为根据,道以自然为根据。
老子的这些话,也说明他认为所谓“万物”,其本质,不过是“一,二,三”等数字的不同表现形式而已。其思想实质,与毕达哥拉斯“万物皆数”的观点,何其相似乃耳!
除了老子以外,中国古人也赋予“数”以特殊意义。如“天数”“气数”“定数”等。把国家兴亡、事业成功与否、人的寿命长短与数字联系在一起。
老子的这种“三生万物”的思想,对中国古代的算学,影响至深。在周朝,作为教育的科目有六种:礼、乐、射、御、书、数。把数学用一个“数”来表示。后来的中国古代数学经典著作,从先秦的《算数书》《周髀算经》到《九章算术》,以及宋元时代的《数书九章》《四元玉鉴》,无不都是由问题、算法(术)和答数所构成。将实际问题的内容和结果,都归结为数的运算,而以数字答案作结。这些“算经”,并没有如古希腊数学著作那样,以证明为主形成理论。即使是一些重要的数学定理,如勾股定理、孙子定理等,也都是以数字的特例来表述的。如前者表示为“勾三股四弦五”,后者表示为“三三数之剩二,五五数之剩三,七七数之剩二”。
这里要说明一点,中国古代数学的这种特点,并不能埋没数学的理论价值,只不过是“寓理于算”,数学的理论包含在算法之中。这种算法思想,与现在的计算机的原理(程序化、机械化)一样,对数学的发展同样起了很大的推动作用。
(三)“万物皆数”的现代意义
1.物质的形态,取决于其组成成分的数量特征,观察事物要了解其中的“度”。
万事万物,其存在的形式尽管各种各样,以至于看不见的空气、宇宙尘埃,其形态都有质与量的实在表现。空气,是由各种气体分子组成的,其中主要成分是氮气(约占78%)和氧气(约占21%),其余约1%为氦、氖等稀有气体。每种气体,又是由大量气体分子组成;每种气体分子,又由不同的原子组成,表现为不同的分子量。这里面就有数量关系。地球之所以适合人类生存和居住,其中的一个重要原因就是地球大气中的各种成分比例得当。而其他星球,如火星、金星、水星等之所以没有生物存在,原因之一便是其上的大气成分失当。
所以,我们在观察事物的时候,了解其中的“度”,是很重要的。这个“度”,就是数量的界限。例如地球上的氧气的含量,过多或者过少都将威胁人类生存,这就是“度”的重要性。而“度”在一定程度上可以用“数”来表示。
又例如,水有三态——在标准大气压下,在0℃~100℃以内为液态;达到100℃就变成气态(水蒸气);而到0℃以下,水就变成固态——冰。所以,水的三种形态,取决于温度度数的多少。这也是“万物皆数”的一个直观说明。
在日常生活中,有“凡事要做到心中有数”的古训。就是说,万事万物都有质与量两个方面,超过了某一个限度(可以用数来表示),事情就要发生质的变化。就如水的形态一样。这方面的教训太多。“心中有数”是人们在长期的生活经验中总结出来的经验教训。如果办事“心中无数”,就要犯错误,出毛病,把事情办砸,事倍而功半。如果做到“心中有数”就能事半而功倍。
即使是在文学作品中,亦是如此。后面我们会举出多个事例来说明。(https://www.daowen.com)
2.事物或事情力量的对比,包含数量特征。
任何事物,都是由互相矛盾的两个方面组成的,即所谓“一分为二”。但这两个方面,并不是完全对等的,是由二者的力量对比而决定的。例如,战争的对立双方的态势,是由双方军事实力决定的。但是双方力量的对比,又不断变化。当主要方面的力量逐渐减弱,次要方面的力量逐渐增强,就可能改变双方的力量对比,使原来的主要方面,降低为次要方面,而原来的次要方面则成为主要方面。中国的抗日战争,就是最好的说明。战争之初,中国处于弱势一方,日军力量远强于中方。而经过几年的战争进展,加上国际势力的介入,日军力量逐渐消减,中国军力则逐渐加强。到了最后阶段,中国在国际反法西斯同盟国的支持下,转败为胜,终于使日军战败投降。这场战争双方力量对比的变化,不是虚假的、空洞的、无根据的,而是双方军队、武器、人力、物力等因素,在数量上对比的变化所表现出来的。
任何其他事物的发展进程,也是由具体事物的数量上的变化而实现的。例如中国现代化建设的发展成就,不是凭空“吹”出来的,而是由一系列的物质生产数字构筑起来的。所谓“由数字说话”,就是这个道理。从各种物质产品逐年产量增加,就可以说明生产的发展速度和现代化的进程。
3.用数字说话,可以使人信服。
任何事物的发展,大至一个国家,小至一个人,都是由一系列物质数量的变化构成的。一个国家的实力,要看其经济总量、生产力的水平、国家的总人口,以及人口的年龄构成比例、劳动力的效率、消费者物价指数(CPI)等具体数据。中国被世界认可为全球第二大经济体,就是通过对中国经济总量的测算所得出的数据说明的。
就以一个人的成长过程来看,也是由一系列数字来反映的。他几岁入学,读过几年小学,几年中学,成绩如何,几岁上大学,读了几年大学,几年研究生,等等,都要用数字来说话,不能无根据地凭空胡说。用数字说话,能检查论点是否真实可信,能使人相信论点。
一个人的健康状况如何,也是由身体检查得出的一系列数据来决定的:身高、体重、血压、血脂、血糖、血液酸碱度以及各种成分数据,身体各种微量元素的数量等等。亦即人的健康是由数字说话的。
青年人报名参军,身体条件需要用体检报告来证明。尤其是空军飞行员的体检,要严格得多,需要的体检项目更多,需要的体征数据更多。即需要更多的数据,才能证明这个人是否能做飞行员。
由此可见,“心中有数”的论断,在当今的信息社会里,更有显著意义,因此也更加重要。
4.如果心中无数,那么就可能犯错误,办事出问题。
我们先来列举与数学有关的文学作品。
例1.唐代著名诗人白居易的著名长篇古诗《琵琶行》,是列入高中语文课本的好诗。但是它在序言中却说错了话,有数字上的错误。他在诗前的序言中说:“元和十年,……是夕始觉有迁谪意。因为长句,歌以赠之,凡六百一十二言,命曰《琵琶行》。”其中所说的“言”,就是指“字”,意思是说这首诗共612个字。这数字说得对吗?
这诗是七言古诗,每句皆为7个字,共有88句,总数的末尾数应该是6,怎么会是2呢?计算一下:7×88=616。果然,全诗共有“六百一十六言”才对。怎么算少了四个字呢?那只能说,这是白老先生的大意和疏忽,没有做到“心中有数”。
例2.当代电视剧《党员二楞妈》中有一个情节:二楞妈因为砍了公家8棵树,被县林业局罚款3000元。她经过调查,发现林业局干部自己偷砍了89棵树,于是便告到县里,要求按照罚她的标准来处罚林业局的这些人。提出应该对他们罚款27600元。
对不对呢?她算错了。你想:8棵树就罚3000元,那么80棵就应该是罚30000元,加上9棵3000÷8×9=3375(元),合计应该罚他们33375元才对。二楞妈少算了5775元。对于二楞妈来说,这可不是一个小数目啊。按道理说,她不会这么宽待林业局干部的,那为什么会少算呢?该不是有意丑化二楞妈“不识数”吧?不会。因为二楞妈是个正直的党员,是电视剧中的典型正面人物,第一主演。那是什么原因呢?——只有一种可能:是该电视剧的编剧们“心中无数”所致。
这说明,即使是编电视剧,也要做到“心中有数”才行!
5.数字和数字技术。
数字,即表示数目的文字,如一、二、三、1、2、3等,都是数字。数字除了用来做数学计算以外,作为独立的文字,还有特殊的用处。其实,数字作为一种技术的应用,古已有之。只不过是人们没有意识到罢了。下面略举几例。
例1.用数字来给书籍编写页码。
给图书的每一页按照先后顺序用正整数来编号(编页码),是最常见的数字技术。但就是这简单的数字技术,古代文人却不会应用。
中国在东汉蔡伦改进造纸术以前,是用竹简和木简来作为书写材料的。竹简、木简,是在竹片或木片上,用刀刻文字或符号,来进行思想表达和记录史实,亦称为“简书”。例如,西汉司马迁所写的《史记》,最初就是用竹简写成的竹简书。竹简书,虽说是一部书,实际上是用麻绳穿起来的一卷竹简(所以古代书籍以“卷”计数,而不是“本”)。据说汉武帝每天所看的大臣奏折,有两大筐之多,要由两人抬进宫来。
但是,竹简书有一个缺点,如果时间长了,一旦穿竹简的麻绳断了,竹简书就散成没有次序的一把竹简,那就很麻烦了。在考古工作中,现代出土的古代竹简书,就遇到这样的麻烦。因为当时的竹简书没有编页码,穿绳烂掉,就不知道竹简的顺序,一捆竹简就不称为一部书了。虽然经过专家们研究,根据每根竹简的内容进行调整,但还是很难完全分辨清楚前后顺序,从而可能造成页码颠倒、错乱。这种错乱,在考古学上有一个专门的名称,叫做“错简”。可见用数字(正整数)给书的页码按照顺序编号,就是很重要的一种数字技术。古人没用这项技术,就给今人造成很大的麻烦。据说湖北几十年前发现的先秦时期的古算书《算数书》,就因为错简,考古人员用了多年时间,才弄清楚前后顺序,刊发出来。
例2.用数字给剧院、影院的座位编号,给体育场的座位编号等。试想,如果不给剧场或体育场的座位编号,不给对应的观众座位票编号,那么,观众就没法确定座位,演出和比赛也没法有序进行。
例3.为一个单位的办公场所、居民的居住小区设置门牌号码,也是数字技术的应用。虽然简单,但若不这样,众多外形、结构相似的楼房会给人们进行空间定位带来许多不便。
例4.八卦和二进制数码。
我们通常用的是十进制计数制度,即用十个不同的数字,代表十个数,进行计数。现在世界上大多数地区的通用数码字,大多是印度-阿拉伯数码0,1, 2, 3, …, 9。这是因为人类在远古时期,最初都是用十个手指计数,故用十进制最为方便。而且印度-阿拉伯数码,大多是一笔写成的,故使用和书写简单便利。但是,除了十进制以外,人类还用过其他计数制。如古巴比伦人用过六十进制;古罗马人用过五进制和十进制混合计数法;古代英国某些部落用过十二进制;玛雅人用过二十进制;等等。17世纪德国数学家莱布尼茨创用了二进制。二进制的好处是,只需要两个符号来计数,就够了。
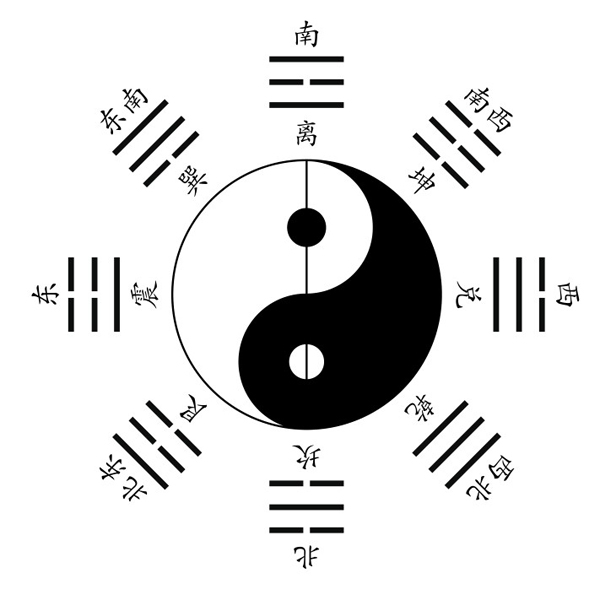
图3-1-3 八卦图
其实,在3000多年之前,中国古人发明的八卦,就已经有二进制的思想萌芽了。传说“文王画卦”,公元前1100年,周代开国之君周武王的父亲周文王在被商纣王囚禁期间,创用耆草表示出阴爻(--)和阳爻(—)两个符号(称为两仪),两两排列出不同的四种形式(四象)。再将四象加上一爻,排列成八种不同排列,而称为八卦。若再将这八卦两两组合,便得出了六十四卦。
当时人们就用这种卦象,进行占卜,对一些重要的大事件,进行预测,希求上苍给予人们以启示。特别有趣的是,在这八卦之中蕴含了二进制的初步思想。它包括了所有前64个三位二进制数,很了不起。17世纪,进入中国传教的西方传教士,将中国八卦传入欧洲,并被正在研究二进制的数学家莱布尼茨了解到,使莱氏大喜过望,认为二进制早已被3000多年前的中国古人发现,十分惊叹,并写信给当时中国执政的康熙皇帝,建议中国应该成立科学院,进行科学研究。
