数学是思维的体操、智慧的催化剂
四、数学是思维的体操、智慧的催化剂
按照我国著名科学家钱学森对学科的划分,数学既不是人文科学,也不是自然科学,而是一个独立的学科,就其研究的对象和模式,应该属于思维科学。著名革命家和思想家加里宁(1875—1946)直截了当地说出了“数学是思维的体操”这句名言。实际上,与其他学科相比,数学更加注重对人们思维的训练。
人类因能够思维,能够使用生产工具,而从动物群体中脱颖而出,成为动物之“王者”。但是人的思维能力和聪明程度,是有区别的。固然思维能力受先天的基因基础影响,但后天的培养和接受教育,对其影响更大。数学家华罗庚说过:“天才在于积累,聪明在于勤奋。”被认为是20世纪最聪明的科学家的爱因斯坦也说:“我没有什么特别的才能,不过喜欢寻根刨底地追究问题罢了。”
其实一个人所谓的聪明和才能,不过是善于思考,喜欢寻根刨底地追求问题的解决。而“学问”本身,也就是一“学”二“问”,而学和问,都需要接受教育(家庭教育和学校教育),并养成习惯,坚持不懈。
接受教育,当然说的是德智体美劳的全面教育。就学校课程学习而言,也是要学习各种文化课程和科学知识。为什么要特别强调数学学习的重要性呢?这是因为数学学习可以帮助人掌握思维形式和思维活动的规律。
人的思维,大致分为三种:形象思维、抽象思维和灵感思维。而这三者是递进关系。特别是灵感思维,是人的创造性思维,是高级思维活动,是人的智慧的表现。而智慧则是人最宝贵的素质和品质。数学则是人的智慧的催化剂。
(一)何谓智慧?
智慧,是人们经常说的一个词语。但是,要问“究竟什么是智慧?”却有多种不同的理解。通常人们的理解是:智慧就是智商和聪明。《辞海》上的解释是:“对事物能认识、辨析、判断处理和发明创造的能力。”在佛教经典中,将梵文“般若”翻译成智慧,其本义为“如实了解一切事物”。
这样解释,把智慧与能力、智力混为一谈,并没有把智慧的真意说明白。为了把智慧与知识、能力区别开来,我们不妨从“司马光砸缸”这一著名的历史故事说起。
相传北宋政治家、文学家和历史学家司马光,小的时候和许多小孩子在一起玩耍,其中一个小孩不小心,翻入一口大水缸中。如果不及时去救起这个小孩,那么,时间一长,他就必死无疑。
这是一个常识,也是一种知识。正是因为有了这种知识,所以大家着急。要是没有这种知识,是不会有人着急的。

2-4-1 司马光砸缸
这时,如果有人跳到水中把这个小孩救起来,或者用某种工具,从水缸里把孩子捞上来。那么,这就是一种技能。
而司马光却用一块石头,把缸砸破,让水流出来,小孩自然得救。这就是智慧的表现。从这个故事中,我们可以清楚地看出:知识、技能(能力)和智慧相比,是不同层次的概念。与知识、技能相比,智慧是更高层次的内在本领,只有少数人才具备的高级能力。
这个故事还可以帮助我们理解智慧所表现出来的特征:
第一,智慧,只有在解决困难问题时,才能表现出来,它是动态的,而非静态的。
第二,灵活运用简单的知识和方法,巧妙地、出乎众人意料之外地解决问题,才是智慧。
第三,智慧是一种高级思维——灵感思维活动。运用智慧解决问题的方法和途径,是非常规的、独创的、前人所没有发现过的,而且基本上是不能重复的。
通常人的思维分为感性思维和理性思维。而灵感思维,是超越了这两种思维,而又综合了这两种思维的高级思维方式。一个人只有在经过长期的、紧张的思维过程之后,才会出现灵感思维。在灵感思维的过程中,才有可能闪现出智慧的火花。
在当今“知识爆炸”的时代,对于我们每个人来说,增长智慧比增长知识和技能,更为重要。
知识和技能,是大多数人通过相关课程的学习,能够学到和掌握的,只是各人领会和掌握的程度有所不同罢了。而智慧,却是无法在课堂上学到的。因为,智慧“只能意会,不能言传”。
(二)我们怎样才能获得智慧和增长智慧?
首先,要学习和掌握多方面的基本知识和技能。因为知识和技能虽不是智慧本身,但却是智慧生长的基础。知识越多,知识面越广,基本技能越熟练,产生智慧的基础就越深厚。古人说“熟能生巧”,就是这个道理。没有知识,或知识较少的人,在现代社会里是谈不上有什么智慧的。
其次,要勤于思考,善于思考。我们平常所学的知识,都是事物的一个断面,是静态的,而且各不联系。我们学习以后,要将各种知识联系起来,加以分析和综合,使所学知识在我们的大脑中“联动”起来。这样才有可能产生新的知识板块和新的知识结构,才能在已有知识的基础上有所发现、有所发明、有所创造、有所前进。
最后,要勤于动手,勇于实践,在实践中解决问题,尤其是困难的问题。知识本身是死的,只有在解决实际问题的实践中,才能将知识越用越活。“活”用知识,才能够激发出智慧。
一般来说,在解决困难问题时,要综合运用多方面的知识,采用各种方法和手段,探索解决问题的多种途径,进行艰苦的、长期的、紧张的思维和动手试验,以至多次反复。这样才有可能“急中生智”。这个“急”,就是指人的思维处于高度紧张状态之中。而这正是出现灵感思维的必要条件,是产生智慧的良好环境。
数学是思维的科学,是人们,特别是青少年思维的体操。所以,数学学习,是提高人们思维能力、激发灵感思维、培养智慧的重要途径。
数学智慧,是指在数学学习活动——实际问题的数学解决中,所表现出来的智慧。这在数学史上有许多精彩的典型事例。例如,中国古代数学家祖冲之巧测冬至点,刘徽创设立体模型——牟合方盖,以求解决球体积计算问题;古希腊数学家阿基米德用力学方法解决数学问题,欧几里得的公理化方法;近代数学家欧拉“图”解哥斯尼堡的“七桥问题”,哈代用初等数学方法解决令人们困惑的“色盲遗传”难题;等等。
历史是一面镜子。数学智慧的这些精彩事例,虽然不能重复,很难模仿,却可以给后人以极大的启示。我们在学习数学的过程中,可以借鉴前人和古人的经验。对于科学史上运用数学智慧解决难题的成功之例,我们要仔细思考,悉心体会这些伟大数学家解决难题的思想方法、活用知识的窍门,学习他们锲而不舍的钻研精神,学习他们攻坚克难的勇气和实事求是的科学态度,以及他们不囿于前人成法、独辟蹊径的创造精神,从而激发和提高我们创新思维的意识和能力,增长解决问题特别是解决困难问题的勇气和才干。这对于我们有重要的“启智”作用。
与其他学科中的问题相比,数学问题中的难题最多,所以对那些思想活跃的青年学生来说,最具有吸引力。青年学生的思想就是这么奇怪:越是困难的问题,越是能够吸引他们的研究兴趣,提高他们的关注度。同时,研究数学问题,无须什么设备和条件,只要有一张纸、一支笔和一个头脑即可,因此也最容易进行。哥德巴赫猜想、费马定理等世界著名难题,能够吸引那么多人的关注和兴趣,能够那么长久地被人们孜孜不倦地研究,就是例证。(https://www.daowen.com)
此外,我们所面临的实际问题——社会生产和生活中的现实问题,特别是那些困难问题,都可以用数学知识、数学方法来解决,即所谓“数学地”解决。
正因为如此,在数学学习和研究中,激发人们灵感思维的机会越来越多。学习数学,运用数学思想和数学方法来解决问题,特别是那些困难问题的数学解决,是人们增长智慧的最好、最为简便、最有成效的方法。
让我们在前人和古人智慧的昭示下,在数学学习和问题解决的活动中,培养自己的思维能力和创造能力,增长智慧。
数学思维之美,其最高表现形式,是数学逻辑证明之美。我们举出历史上著名的两个数学证明例证,就可以略见一斑。
例1.证明素数有无穷多个。
这是古希腊时期提出并被证明的难题之一。素数,是除了1以外,只有1和它本身两个因数的正整数,如2, 3, 5, 7,11,13, 17,19, …可以不断列举下去。但是要证明没有最大的素数,或者说素数有无穷多个,就牵涉到无穷,便成为一个非常困难的问题。欧几里得在《几何原本》中给出如下巧妙证明,既简洁,又无懈可击。证明如下:
用反证法:假如素数不是有无限个,而是只有有限个,那么就可以假设素数有n个:p1, p2, p3, …, pn。那么这几个素数的乘积加1,即N=p1p2p3…pn+1必然也是一个正整数,因此它不是素数就是合数。
因为N是两项之和,两项应该有相同的因数。它的前项是所有素数之积,故能被任何一个素数pn整除,但是N的后项是1,显然不能被任何一个素数整除。这是个矛盾,这说明N不能被任何一个素数整除。但是已经假设,所有素数都尽在于此,所以,N除了它本身外,没有素数因数,所以它必然是素数,而且与所有素数p1, p2, p3, …, pn都不同,即它是一个新的素数,而这与素数只有有限个的假设相矛盾。既然素数不是只有有限个,当然就有无限多个。命题便得到证明。
例2.证明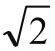 不是有理数(即是无理数)。这也是欧几里得证明的。
不是有理数(即是无理数)。这也是欧几里得证明的。
证明也是用反证法。证明如下:假设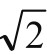 是有理数,便可设为一个分数,不妨设
是有理数,便可设为一个分数,不妨设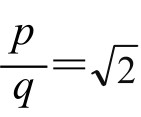 (既约分数)。
(既约分数)。
将等式两边平方,得2q2=p2,于是p2应是偶数,因此p也是偶数。等式两边约去2,由此推出q2也是偶数,故q也是偶数。既然p、q都是偶数,那么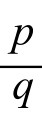 就不会是既约分数,与假设矛盾。这个矛盾说明假设错误,即
就不会是既约分数,与假设矛盾。这个矛盾说明假设错误,即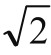 不可能是一个既约分数,所以
不可能是一个既约分数,所以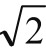 不是一个有理数,而是一个新数,称之为无理数。
不是一个有理数,而是一个新数,称之为无理数。
从以上两个数学难题的证明,可以看出数学逻辑证明之简洁明了,而且不容置疑。除了数学方法之外,用其他任何方法和手段,都不可能进行说明,更不用说是证明了。
我们学习数学,应该重视数学问题的研究和解决,因为问题,被普遍认为是“数学的心脏”。不仅如此,问题还是数学趣味的源泉。许多数学家、数学爱好者,都是因为对解数学题目着迷,而爱上了数学,从而选择数学作为终生奋斗的事业。
首先,数学的内容就是由问题组成的。数学定理是问题,数学公式是问题,数学例题、习题更是问题。没有问题,就没有数学。
学习数学,如果不做题目,那就等于没学。数学教师,如果不会解题,那就是不合格的数学教师,是不会受学生欢迎的。
其次,数学问题是推动数学发展的动力,数学理论正是在解决问题——理论问题和实际问题中前进的。研究数学,就是为了不断研究问题、解决问题——数学自身的问题和现实世界提出的问题。
20世纪之初,由希尔伯特在世界数学家大会上提出的23个数学问题,开启并主导了整个20世纪的数学研究,吸引了全世界数学家的目光,在某种程度上左右了百年来世界数学发展方向。多少数学家被这些问题所吸引,为研究这些问题而痴迷。
最后,数学与文学虽有巨大差异,但也有相通之处,即对于真、善、美的追求是相同的。数学中的问题好比是文学中的诗歌,都是人类思维的精华所在。一首经典好诗,可以长久地萦绕人心,让人终生不忘。其吸引人们心志的魅力,只有数学问题可以相比。一个数学问题也可以长久地存放在人们的脑海中,魂牵梦绕,昼思夜想,非求得解决不可。而且数学题越做越想做,越做越有趣。

图2-4-2 中国数学家华罗庚
我国著名数学家华罗庚,就是从做初等数学题起步,最终成为一代数学大家。陈景润为解决“哥德巴赫猜想”而废寝忘食,不顾“文革”中遭受的迫害,在夜深人静时,趴在厕所墙头上利用那盏小灯的微光,孜孜不倦地在草稿纸上埋头计算。是什么力量促使他能够在如此艰苦的条件下,如此长时间地努力奋斗呢?这只有一个解释:数学问题的魅力实在太大!
我国另一位著名数学家杨乐,于1979年在安师大教学大楼,为芜湖市中学生做过一次科普报告。他在回答学生“您为什么选择数学作为终身职业”的提问时说:“我对数学的兴趣,产生于中学时代,我在证明三角形垂心定理时,发现了书本以外的一种新证明方法,受到数学老师的肯定。这使我对数学产生了浓厚的兴趣和学习数学的信心,最终使我在报考大学时,选择了数学专业。”
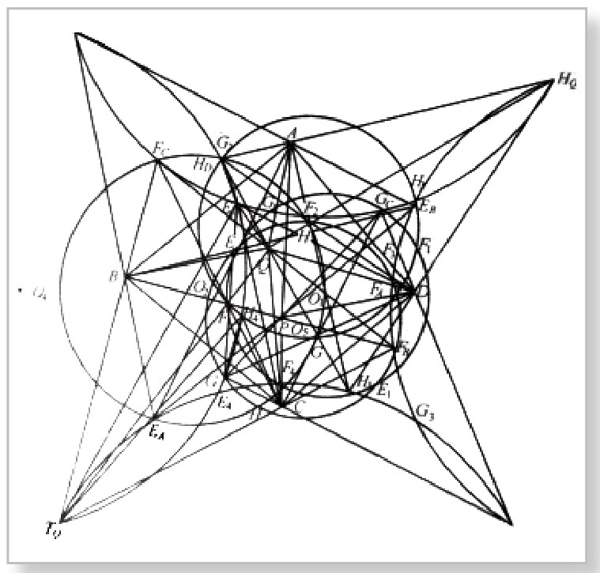
图2-4-3 尚强主编《几何题解》中的图形之一
另一个例子是安师大附中的一个学生,一个对数学痴迷的数学爱好者——王枫。他从初中一年级开始,就利用双休日到书店看高等数学书籍,一年以后,他就读完了微积分、高等代数、解析几何和半本复变函数,而且会做其中的习题,这说明他确实已经读懂了这些高等数学内容。上高中后,他两次进入中国数学冬令营,后被北大数学学院破格选录。他现在早已博士毕业,在浙大数学研究所工作。有人问过他为什么如此痴迷数学,他说是因为在小学参加数学竞赛时,受数学老师指导,做了不少有趣的题目。从此就爱上了做数学题,越做越觉得有趣。家里没有数学书看,就到书店里去看,看上瘾了。
本书作者之一——尚强本人,也是因为在少年时代就喜欢做几何题目,而爱上数学,现在还喜欢琢磨几何难题。其他许多数学爱好者的经历,也都能够证明:数学问题,确实具有特殊的魅力,是数学趣味的源泉。
数学问题本身,富含多层文化意义,承载多种人文精神。所以,在数学教学中不应排斥做数学习题。相反,应该发扬数学问题中的文化意义和人文精神,把解决数学问题作为一种研究来对待,使学生从中不仅获得数学知识,而且还能获得智慧,获得文化享受。
当然,在数学教学中,对待数学题,不能简单地重复练习,更不能搞“题海战术”,不是做题越多越好。
做数学题,首先要对数学题有所选择。题目要扣人心弦,解题要讲求思想方法,讲解解题思路要能够引人入胜,使人听了如沐春风。数学证明过程,要合情合理,令人口服心服。
数学问题,虽然并不都是现实世界的实际问题,但是即使是纯理论题目,也一定有实际背景和理论来源。而理论来源归根结底是现实问题的反映。也就是说,数学问题,大多数是现实的、具体的实际问题的模型,是其他领域里出现的问题的典型。因此,解决数学问题,可以帮助人们去解决其他领域的现实问题,可以启发人类智慧,帮助人们在科学研究中攻坚克难。所以数学解题研究本身,可以触类旁通,开启人类的心智,间接地助推社会前进。
因此,在文化数学的建设中,应该高度重视数学问题的开发,以及解题研究方法,使得问题解决(即做数学题)能够在更大的程度上激发学生的智慧。
