飞越北极的北京—纽约航线
九、飞越北极的北京—纽约航线
2001年7月16日新华社报道:此前一天,7月15日,我国首次开辟“极地航线”——北京—纽约航线,途经蒙古、俄罗斯、北极地区和加拿大。此“极地航线”比原来航线缩短了一个多小时的飞行时间。关于“极地航线”可提出两个数学问题:第一,连接北京、纽约的“极地航线”的最短航程是多少?第二,这条最短的“极地航线”与北极点能够接近到什么程度?
第一个问题,是求球面上两点间的球面距离,这是一个常见的数学问题。第二个问题,是求球面上一点到一个大圆弧的球面距离,这是一个不常见的问题。我们可以用中学课本中的知识来解决它。
为此,我们首先要分析一下已知条件——北京和纽约的经纬度为北京(北纬39.9 °,东经116.4 °)、纽约(北纬40.9 °,西经73.7°),为简化计算,可以视为都在北纬40°线上。北极点N是纬度的极点,那么将两个问题化为数学问题:
(1)求A(北京)、B(纽约)两点间的球面距离;
(2)N点到大圆弧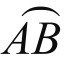 的球面距离。
的球面距离。
解:这是球面几何问题,需要有关球面几何与球面三角知识。
设球心O,连接OA、OB、ON,构成三面角O-ABN。又设∠AON=α, ∠BON=β, ∠AOB=γ,球面△ABN的三个球面角分别为A、B、N。
在图4-9-1上,我们考虑以O为顶点的三面角O-ABN。
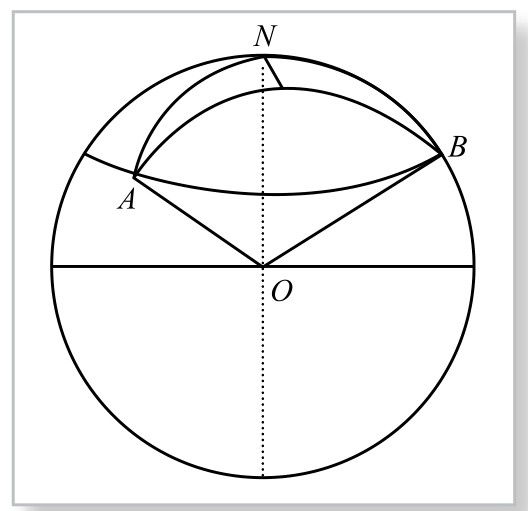
图4-9-1
已知面角α=∠AON=90°-39.9°=50.1°, β=∠BON=90°-40.9°=49.1°,二面角A-ON-B=∠N=360°-(116.4°+73.7°)=169.9°;地球半径R=6370km。
这本来是球面三角的问题,我们要把它化为立体几何中的三面角的问题来解。为此,先推导有关三面角的两个有用的公式。
如图4-9-2,在三面角O-ABN中,设OA=R, ∠BON=β,∠AON=α, ∠AOB=γ。
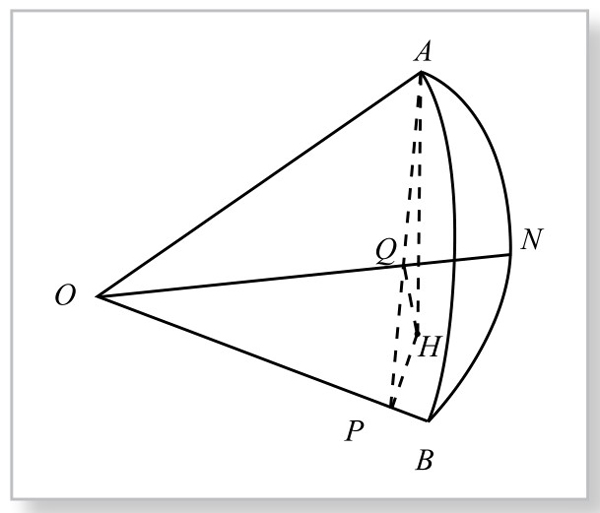
图4-9-2
过A作对面垂线AH, H为垂足;过H作HP⊥OB,作HQ⊥ON, P、Q分别为垂足;连接AP, AQ。则N=∠AQH为二面角A-ON-B的平面角,B=∠APH为二面角A-OB-N的平面角。
折线OQHP在OB上的射影,等于OQ、QH、HP在OB上射影之和,等于OP。而HP在OB上的射影为0, OQ、QH在OB上的射影,分别为
OQ cos β=OA cos αcos β=Rcos αcos β;
QH cos(90°-β)=AQ cos Nsin β
=OA sin αcos Nsin β
=RsinαcosNsinβ
所以,Rcos α cos β+R sin α cos Nsin β=OP=OAcosγ=Rcosγ。
约去R,便得三面角的余弦公式:
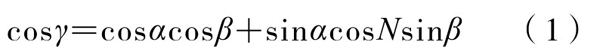
它可以和平面三角形的余弦定理相类比。
另一方面,考虑到AP、AQ在AH上的射影相等——都等于AH,容易得到APsin B=AQ sin N, OA sin γ sin B=OAsin αsin N,或sinγsinB=sinαsinN。同理可得sinαsinN=sinβsinA。
由此得三面角的正弦公式:
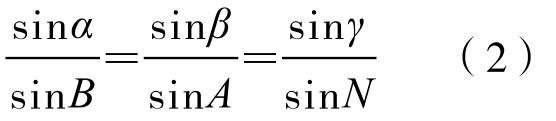
它可以类比于平面三角形的正弦定理。
现用公式(1)和(2)来解决我们的问题。
1.求A、B两点间的球面距离,即大圆弧(劣弧)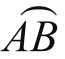 的长。
的长。
将有关数据代入(1)式,有
cosγ=cosαcosβ+sinαcosNsinβ
=cos50.1°×cos49.1°+sin50.1°×cos169.9°×sin49.1°
=-0.1508951
查反余弦函数表得γ≈98.6788°。从而
大圆弧(劣弧)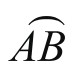 的长=
的长=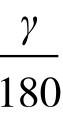 ×π×6370≈10970.86(km)。(π≈3.1415926)
×π×6370≈10970.86(km)。(π≈3.1415926)
连接A, B两点间的小圆弧,近似地等于北纬40°的纬度圈在这两地之间的一段弧长:
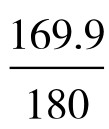 ×π×6370×sin50°≈14469.854(km)。(π≈3.1415926)
×π×6370×sin50°≈14469.854(km)。(π≈3.1415926)
显然,它比AB间球面距离长了约3500 k m。即极地航线比沿北纬40°航线缩短约3500 km。
2.求N点到大圆弧(劣弧)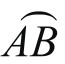 的球面距离。过N点作大圆弧与
的球面距离。过N点作大圆弧与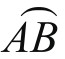 直交,交点为K。先在三面角O-ABN中用公式(1)将有关数值代入,求二面角A:
直交,交点为K。先在三面角O-ABN中用公式(1)将有关数值代入,求二面角A:
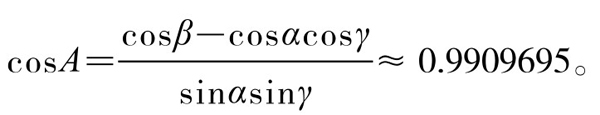
查表得A≈7.7°。
在三面角O-ANK中设∠NOK=ω,二面角A-OK-N为直角。将有关数值代入公式(2),得:
sinω=sinαsinA=sin50.1°×sin7.7°≈0.1027895
从而查表得ω≈5.9°。大圆弧(劣弧)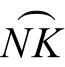 ≈656(km)。这就是北极点到最短“极地航线”的球面距离。
≈656(km)。这就是北极点到最短“极地航线”的球面距离。
可见,这条最短“极地航线”已经深入北极腹地,离北极点非常近。
本章所述,关于数学的大用,只是略举数例。在20世纪70年代,华罗庚先生身体力行,亲自带领“推优小分队”,到全国多个省市和地区,大力推广优选法。本书作者之一胡炳生,作为当年“推优小分队”的一员,在浙江几个地市县,和当地工人、干部一起,运用优选法和统筹法等数学方法,对很多生产环节进行过优选改进,亲眼见到了数学在生产部门和各个环节的指导作用。
正是因为数学“大哉之为用”,所以数学之美,才更加璀璨,更加为人们所赞美。
