借形表数(式)有趣味
七、借形表数(式)有趣味
数学的对象是数和形。数是无形的,而形却能和数处于一个学科之内,这是什么道理呢?原因就在于数与形是可以互相转化的:数里有形,而形中又有数。而若将这种思想运用于解决数学问题中,即能收到化难为易的奇效。请看下面的问题解决。
1.一个纯代数的问题:
解无理方程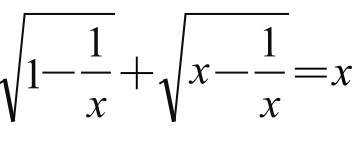 。
。
分析和说明:如果按照常规方法,解无理方程,要用平方来消去根号,使其化为有理方程。这就要经过两次平方,将要出现四次方程。而要解四次方程可就复杂了,且没有一般方法。
我们能否借助作图,来联系几个无理式的关系呢?
虽然这是无理方程,但是其中的无理式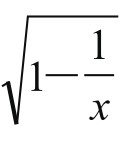 和
和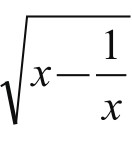 的平方分别与
的平方分别与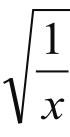 的平方求和,答案却是简单的有理式1和x。这就给我们留下了思考空间。
的平方求和,答案却是简单的有理式1和x。这就给我们留下了思考空间。
若以它们为直角边作直角三角形,那么,其斜边就是1和x。多么简单!具体怎么操作呢?
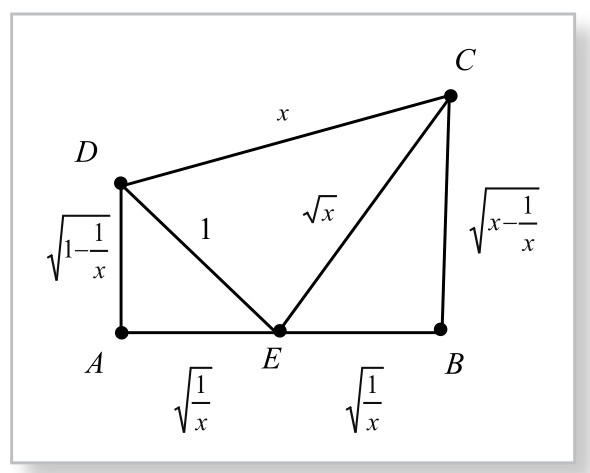
图5-7-1
思考一:以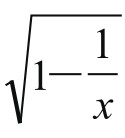 、
、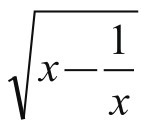 为上下底边,以
为上下底边,以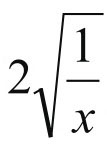 为腰,作直角梯形ABCD,如图5-7-1,则梯形面积为
为腰,作直角梯形ABCD,如图5-7-1,则梯形面积为
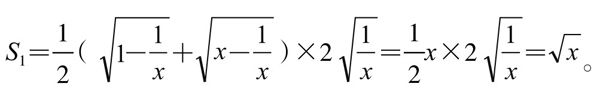
而S△ADE+S△BCE=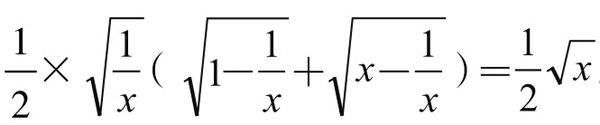 。(https://www.daowen.com)
。(https://www.daowen.com)
由此可见,S△CDE= S1-(S△ADE+S△BCE)=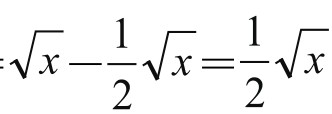 。
。
由勾股定理知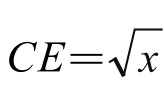 ,DE=1,而S△CDE=
,DE=1,而S△CDE=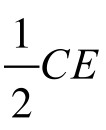 · DEsin∠CED=
· DEsin∠CED=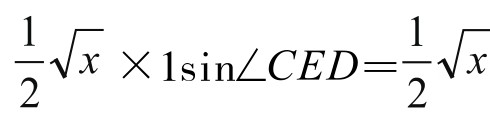 ,所以sin∠CED=1,得∠CED=90 °。
,所以sin∠CED=1,得∠CED=90 °。
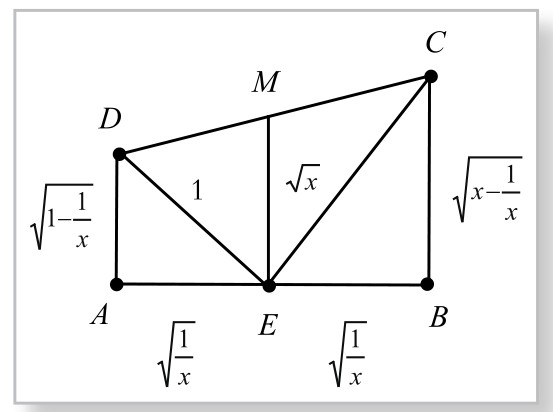
图5-7-2
因此,△CDE为直角三角形。过CD中点M作底边平行线ME,则ME是等腰梯形的中位线,故ME=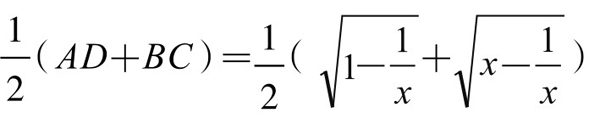
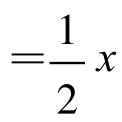 。而ME又是Rt△CDE斜边上的中线,故DC=2ME=x。
。而ME又是Rt△CDE斜边上的中线,故DC=2ME=x。
在Rt△CDE中,用勾股定理,应有CE2+DE2=CD2,即有x+1=x2,这是二次方程,容易解得x=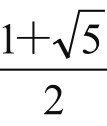 。
。
此亦即所求无理方程之解。
思考二:前面是作等腰梯形,来联系有关的无理式,使无理方程化为有理方程(二次方程)。我们能否将作图简化一点呢?——矩形?三角形?再试一试。
试以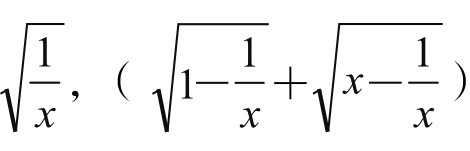 =x为两边,作矩形ABCD,如图5-7-3,其中
=x为两边,作矩形ABCD,如图5-7-3,其中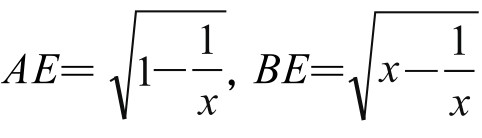 ,连接CE、DE,由上述同样理由,知△CDE为直角三角形,从而得x+1=x2,解得
,连接CE、DE,由上述同样理由,知△CDE为直角三角形,从而得x+1=x2,解得

图5-7-3
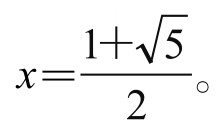
思考三:能否进一步改为三角形呢?试以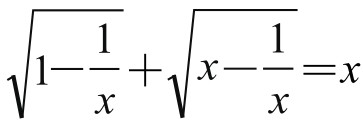 为底边,以
为底边,以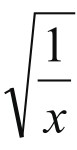 为高,作三角形,如图5-7-4。同样方法,知道所作三角形为直角三角形,于是得到关于x的二次方程:x+1=x2,同样解得
为高,作三角形,如图5-7-4。同样方法,知道所作三角形为直角三角形,于是得到关于x的二次方程:x+1=x2,同样解得
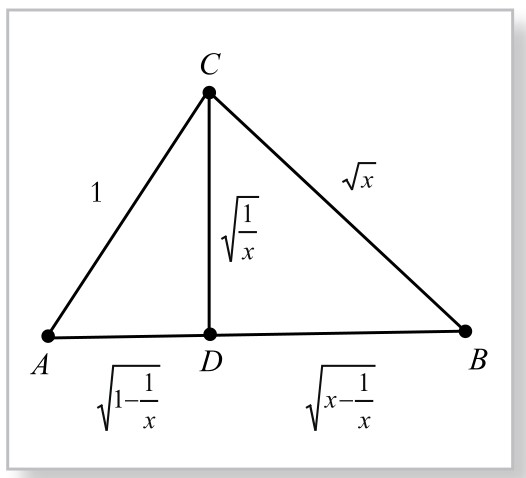
图5-7-4
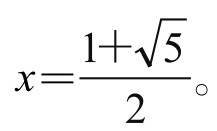
以上三种方法,发现无理方程内在的含未知数x的无理式的有理关系,从而使关于x的无理方程化成二次方程,从而大大简化了原问题。比较三种作图方法,图形的不断简化,使问题的解法越来越简单。
将数量关系转化为形(线段长度和图形面积关系),再将形还原为代数式。从中可以看出形与数的内在联系,多么和谐,多么美妙!许多代数问题和三角问题,都可以如此地去思考,化数为形,形数交融,得到美妙的解决途径。
