简化,简化,再简化
六、简化,简化,再简化
问题的解决,我们希望它越简单越好。因此我们重要的思维原则,就是简单化原则,务使问题的解决方案简化,简化,再简化。如果能将其最后化归成人所共知的基本问题,那么,问题就算解决了。试想一想,我们解题的过程,哪次不是将其不断化简的过程。其实,计算机之所以能够解决那么复杂的数学题,也是简化的结果。因为事实上,计算机只能做最简单的加法——“1+1=10(二进制数)”。而将其他的运算,都化成这种运算的连缀和叠加——用一串简单的运算(程序),来表达复杂的运算。这也就是我们解题的基本策略。
例如,解方程,总是设法将其降低次数,最后化成二次方程。这样,只要利用二次方程求根公式,就一定能够求得它的解来。在解几何作图题时,总是设法运用一连串的基本作图方法来完成它。要解决任何问题,总是从最简单处入手。
(一)简化第一例
问题1(天津市数学竞赛题):
下面哪一个数一定不是某个自然数的平方数(其中n是任意正整数)?
(1)3n2-3n+3;
(2)4n2+4n+4;
(3)5n2+5n-5;
(4)7n2+7n+7;
(5)11n2+11n-11。
这是一个很有意思的经典问题。但如果从大处想,作一般性证明,那就非常困难了。对于这类判断题,通常我们用排除法,逐步淘汰。如果看出了哪个式子是自然数的平方,它就被淘汰了。先以第一个为例。它不是平方数吗?
思考一:二次方程3n2-3n+3=k2(*)没有正整数解吗?
这是二元二次方程正整数解的判定问题,是数论中很难的问题之一,就连一般大学数学教材,都不讲。要一个中学生去做,当然很困难。但如果,在(*)式中取k为具体自然数1, 2, 3,将问题简化成:
思考二:方程3n2-3n+3=1, 3n2-3n+3=2, 3n2-3n+3=3有无正整数解?
这就变成判断二次方程正整数解的存在问题,根据二次方程求根公式,就有办法来解决。虽然稍微麻烦一点,但中学生是能够解决的。
我们再来简化一下,在(*)式中取n为具体自然数1, 2, 3,将问题变为思考三:当n=1, 2, 3时,3n2-3n+3是平方数吗?(https://www.daowen.com)
这就变成一个简单的算术问题,连小学生都能够回答:当n=2时,该式等于9,它是3的平方,故(1)被淘汰。同理,当n=2时,5n2+5n-5=52, 7n2+7n+7=72也是平方数,故(3)(4)也被淘汰。当n=3时,11n2+11n-11=112,(5)也被淘汰。
因此,(1)、(3)、(4)、(5)都被淘汰。最后剩下的(2)必是应选之项。
这里,有人要问:为什么你不对(2)进行直接的检测呢?——其实,在思考和检验的过程中,当然要考虑(2)是否被淘汰。但当令n=1, 2, 3时,它都不是平方数时,是继续令n=4, 5, 6, …去检测它呢?还是暂时放弃它,跳过去呢?聪明的读者,一定会同意后述做法:先将(2)跳过去。因为,如果(2)就是我们要选的,那么,这样去验算,是不会有结果的。我们跳过(2),是灵活性的表现。
从上述的思维过程中,我们看到将原来极其困难的难题,一步步简化成连小学生都能够解决的问题。这不仅仅是解题的技巧,也是解题的思维原则——简单化原则所起的大作用。
问题2(2002年五羊杯初中数学竞赛初三题17):
五羊大学建立分校,校本部与分校隔着两条平行的小河。如图5-6-1,甲、乙表示小河,A为校本部大门,B为分校大门。为方便人员来往,要在两条小河上各建造一座桥,桥垂直于河岸。图中的尺寸是:甲河宽8m,乙河宽10m;A到甲河垂直距离40m, B到乙河的垂直距离20m;两河间距离100m, A、B两点水平距离(与小河平行方向)120m。为使A、B两点间来往路程最短,两座桥都按这个目标而建,那么,此时A、B两点间来往的路程是多少?
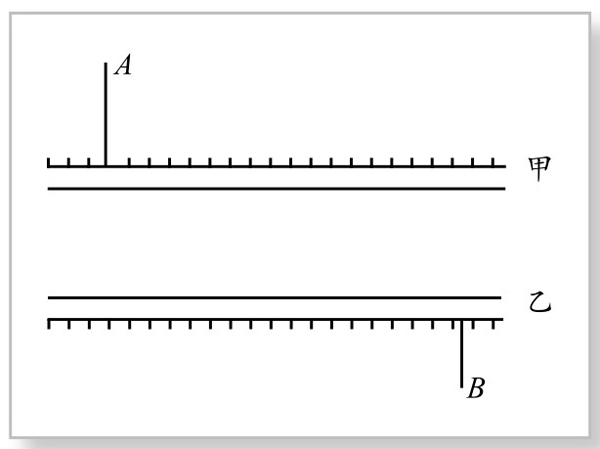
图5-6-1
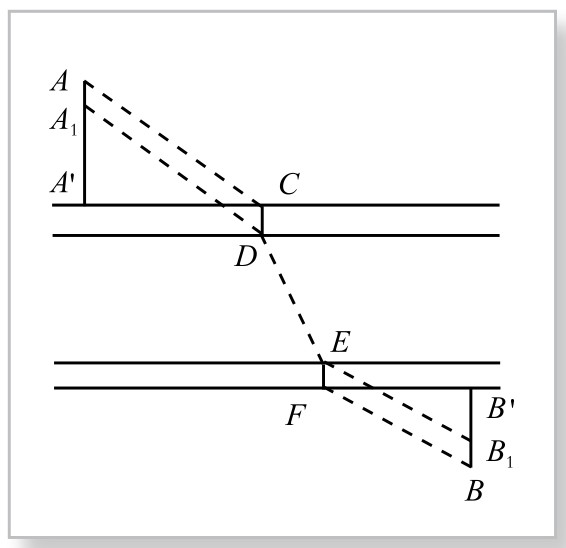
图5-6-2
思考一:设在小河甲上建造桥CD,在小河乙上建造桥EF,则在A、B间来往的路线是折线ACDEFB。若在AA′上取AA1=CD,在BB′上取BB1=EF,连接A1D、EB1,那么,除了桥以外,从A到B在陆地上走的路程,应是折线A1DEB1。因为两座桥的长度是不能减少的,所以A、B间路程的长短,决定于这条折线的长短。显然,当且仅当A1DEB1成一条直线时,从A1到B1有最短距离,因而A、B间有最短距离。这时A1B1与甲河北岸的交点D1,就是甲河的桥址,与乙河南岸的交点E1,就是乙河的桥址。
由此得到计算方法如下:过B1作河岸的平行线,交AA′的延长线于K,如图5-6-3,则易知A1KB1为直角三角形,两直角边A1K=(40-10)+10+100+8+(20-8)=160, KB1=120,斜边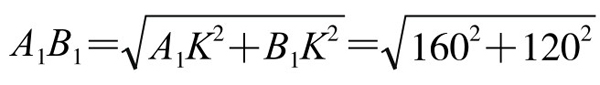 =200。
=200。
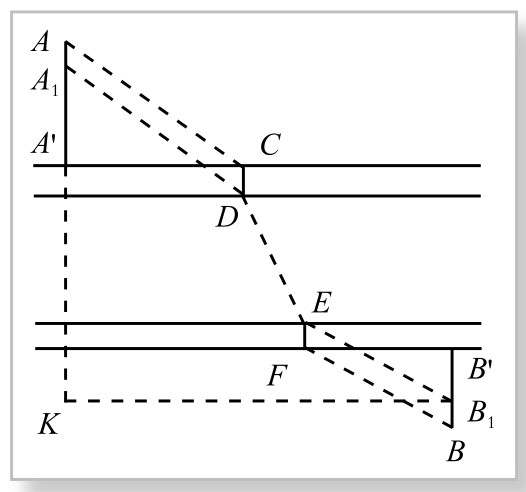
图5-6-3
从而,AB间的最短距离=200+10+8=218(m)。
思考二:设想小河甲与乙,都缩成了一条线(宽度为0),那么,显然A→A1、B→B1。而这两点之间的最短距离就是直线A1B1,如图5-6-4所示,它的长度就是A1B1=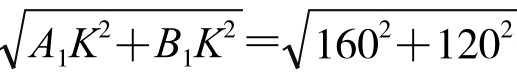 =200。加上两座桥的长度,于是我们问题的答案就是:从A到B的最短路程等于200+10+8=218(m)。
=200。加上两座桥的长度,于是我们问题的答案就是:从A到B的最短路程等于200+10+8=218(m)。
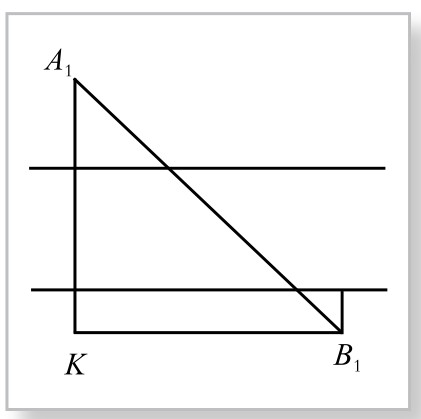
图5-6-4
相比之下,这第二种思路,简单得多,也优美得多。自然,这种优美的简单性,是在经过认真思考后得到的。因此,数学的简洁美,确实具有方法论上的意义。
对于数学简洁美的追求,往往是人们学习数学、研究数学的一种动力。有的数学题本身,就包含了某种因果关系的简单性,在解题中我们揭示出了这种简单性,就能够感受到它的简妙,得到美的享受。
