序方,数字图阵新玩法
十四、序方,数字图阵新玩法
2002年,国际数学家大会在我国召开时,著名数学家陈省身先生为青少年数学爱好者题词——“数学好玩”,这对我们广大数学教师来说,有很大的启发。因为只有使得青少年学生觉得数学“好玩”,才能对它有学习的兴趣;只有对它有兴趣,才能主动地、积极地学习它。怎样才能使学生觉得数学好玩呢?除了联系实际把课本上的数学知识讲得生动有趣以外,还要不断发掘数学中有趣的题材,使其成为动脑筋的数学游戏。序方和序方分块问题,就是这样一种新的有趣的发展性的数学问题。
2002年澳大利亚数学竞赛有这样的一个问题:如图5-14-1,将三阶序方分成3块,每块数字之和(该块的值)都是15;而且每块数字都连成一整块(连通块)。
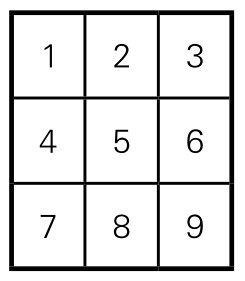
图5-14-1
请注意,这里所说的“序方”,不是常说的“幻方”。
三阶“序方”虽然也是由1, 2, …, 9这九个不同数字组成的数字图阵,但是其中数字的排列,是顺序排列的,没有要求每行、每列数字之和相等。在数学上,相似与相同,有天渊之别。序方与幻方,只是形式上相似,但无论在性质上,还是“玩法”上,都有根本区别。
但是,由“序方”出发,产生的数学问题,却是很有趣的新问题:要把这九个数字所在方格,划分为三块(连通的整块),使得每块所含的数字和相等。
对于三阶“序方”来说,分三块,是个比较简单的问题,只要仔细想一想,便能得出答案:三块的数字组成是[6, 9], [7,8], [1, 2, 3, 4, 5],(如图5-14-2)这三块都是连通的,而且数字和都等于15。
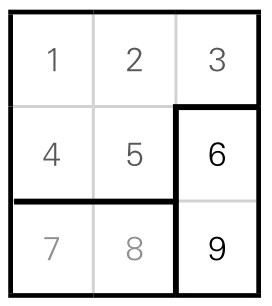
图5-14-2
如若序方的阶数增多(如图5-14-3、5-14-4),提出同样的问题,就不那么简单了。一般地,n阶序方是:由n2个正整数1, 2,
3, …, n2,按照自然顺序,排成n行n列的正方形数字图阵。玩法是:将n阶序方分成m个连通块,使其中每块数字之和相等。这称为“序方等值分块问题”。
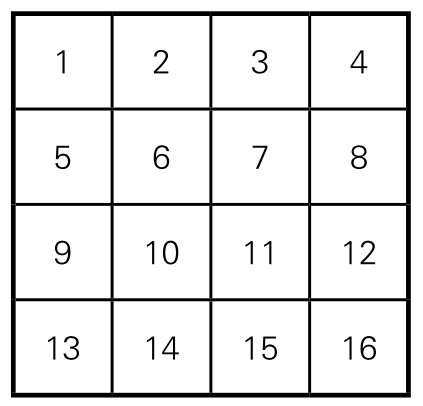
图5-14-3

图5-14-4
序方等值分块问题,是数学家Dijiswa提出来的,被称为“Dijiswa Square”。
关于n阶序方等值分块问题,有两点值得我们注意:
第一,这是一个开放性的数学问题。一般说来,n阶序方不一定都能够进行等值分块;如果可以等值分块,也可能有多种等值分块法。
其二,序方分块中的每一块,尽管可以形状各异,但要求都是要连通,亦即同一块的所有数字都彼此相连。
为方便起见,我们将n阶序方分成等值块的块数r,称为序方的“商”;这时每一块的值,称为该序方的“r商块值”。例如,四阶序方只能分为2个等值块,即四阶序方的“商”只能取2,商值为68。但是其分法不是唯一的。例如,有下面三种不同的分法(图5-14-5至5-14-7):
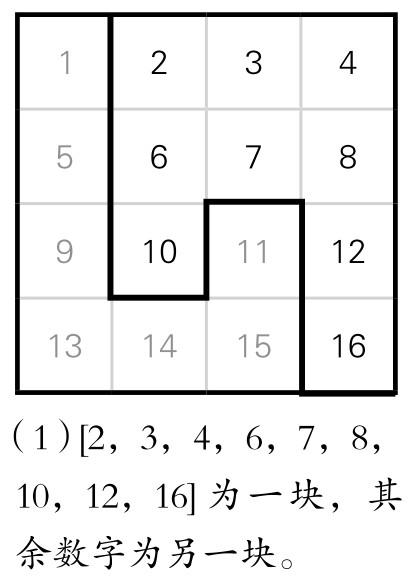
图5-14-5
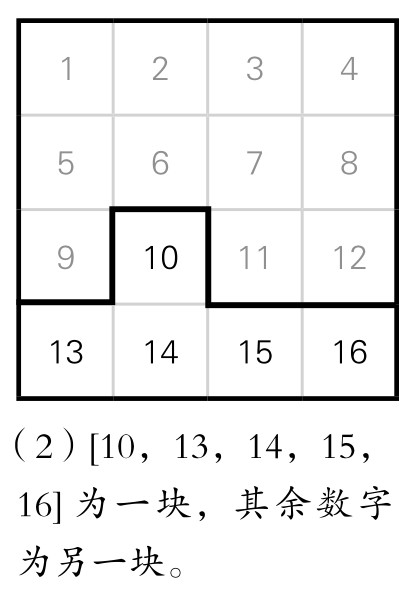
图5-14-6
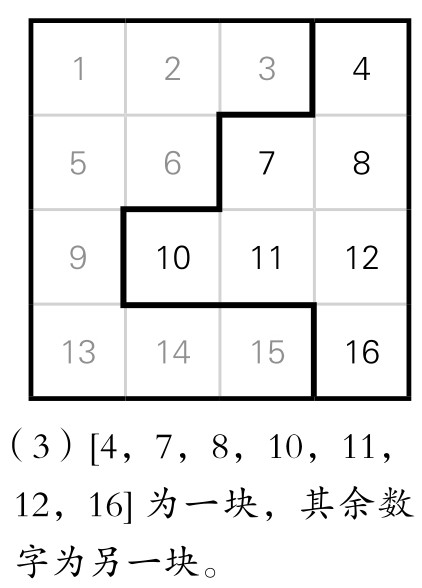
图5-14-7
这样的分块法,是怎么发现的呢?——先盯住最大数字,看与它相邻的数字之和,若不足数,再向外扩展开来寻找合适的数字。到临近商值时,再进行调整:若不足数,则以小换大;若多余时,则以大换小。当然需要照顾到整块的要求。
但并不是任何阶的序方都能够进行等值分块。例如,五阶序方(图5-14-8)则不能进行任何等值分块。事实上,五阶序方中所有数字之和为13×25=325,如果可以等值分块的话,只能分为5块、13块或25块;5块的值是65,13块的值是25, 25块的值是13。但是25与其邻近的几个数字之和,都不可能为65,因此含有25的一块,它的值无论如何都不可能是65,更不可能是13。同样,含有24这一块的值也绝不可能是25。(https://www.daowen.com)
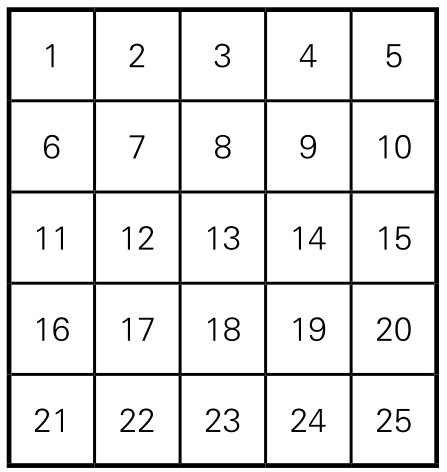
图5-14-8
而六阶序方可以分成3个等值块,等值块的商值为222。有很多种分块方法,例如下面的三种分法(图5-14-9至5-14-11):
第一种分法
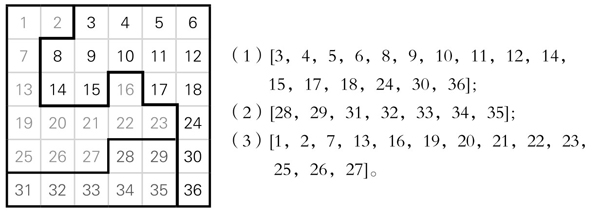
图5-14-9
第二种分法
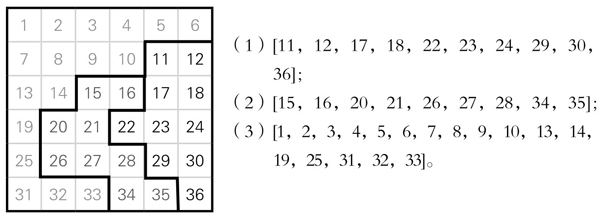
图5-14-10
第三种分法

图5-14-11
除此以外,可能还有别的分法。请读者试着去寻找。
我们还可以进一步提出以下问题:有多少种方法将六阶序方分成3个等值块?可以将六阶序方分成2个等值块,使每块的值都是333吗?可以将其分成6个等值块,使每块的值都等于111吗?等等。
下面我们来讨论八阶序方的等值分块问题。
因为八阶序方所有数字之和是2080,所以八阶序方如果可以等值分块的话,可能存在多种分块法,如下表5-14-1所列:
表5-14-1

(商小于商块值)
下面我们只讨论商数为4的情况。这时的商块值为520。下面给出两种分法(图5-14-12、5-14-13):
第一种分法

图5-14-12
第二种分法
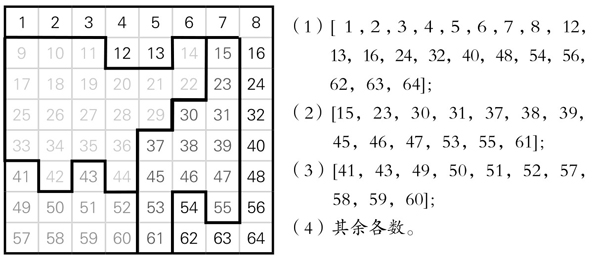
图5-14-13
再讨论商数为2的情况,等值块只有两块,等值块的商值为1040。我们只给出一种解(图5-14-14):
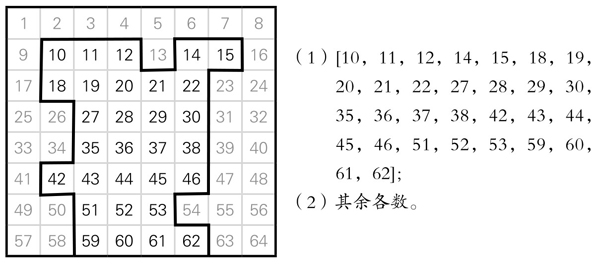
图5-14-14
除此以外,读者还能够给出其他的分块方法来吗?
关于序方,还有其他类型的问题,例如,定值异型块的存在问题。所谓“定值异型块”,就是给予和数为定值的整块区域是否存在。如在八阶序方中,是否存在块值为100的连通的整块区域?作为发展性问题,读者可以自行研究。
