几何图形之美及其应用
六、几何图形之美及其应用
对称图形具有对称美,是人们最容易感受到的形式美。
基本几何图形——直线、线段、等腰三角形、正多边形,圆、椭圆、双曲线、抛物线,以及立体图形中的正多面体、圆柱、正棱锥、正圆锥等,都是对称图形。曲线中的摆线、心脏线、悬链线、双叶线、玫瑰四叶线等,也都是对称图形。直线形端庄,正直;曲线形柔美,舒展。它们都令人心情愉悦。所以许多建筑物,都利用数学中的对称性,进行设计。例如,古希腊的神庙(图2-6-1)、中国的古塔(图2-6-2)等等,大多是对称外形。
图2-6-1 古希腊时代的雅典神庙

图2-6-2 中国宋代的应县木塔
在建筑物的构型上,直线形,可以彰显其雄伟高大,刚劲有力,多见于高大建筑物,如神庙、高楼大厦等;曲线形,则可以突出其优雅柔美,多见于桥梁、高速公路立交桥等建筑。下面列举一些著名建筑物(图2-6-3至图2-6-6)。

图2-6-3 跨越大江的悬索桥,悬索呈悬链线形

图2-6-4 港珠澳大桥——空前的施工难度、顶尖的建造技术

图2-6-5 埃及胡夫金字塔(等腰三角形)

图2-6-6 希腊帕特农神庙
胡夫金字塔和帕特农神庙这两座世界著名建筑物的外形,都是可以放在一个长宽满足黄金比的黄金矩形之中。图2-6-7的加拿大国家电视塔,它的工作大厅的位置也在全塔的黄金点上。这说明从古至今,数学美在大型建筑中都有体现。

图2-6-7 加拿大国家电视塔
(一)数学对称美及其在解题中的应用
时间无头无尾,空间向任何一个方向都可以不断地延伸,而相对的两个方向都是对称存在的。世界万物都是对立统一的,都包含有矛盾的两个方面,这两个方面是对立的。而统一就包含在对立之中。这反映在数学上就是对称性。
正数与负数、运算与逆运算、命题与逆命题、微分与积分,以及对偶定理、对偶命题等等,都是对立统一的,都含有对称的意义,并包含奇异的和谐。正方形、菱形、圆、圆锥曲线等,都是对称图形。数学式子中的对称性,也时有所见,如对称多项式、对称不等式。
在解题时,利用图形和式子的对称性,往往可以收到事半功倍的效果。(https://www.daowen.com)
例1.如图2-6-8,六边形ABCDEF的各个内角相等,且AB+BC=11, FA-CD=3,求BC+DE之值。
分析与求解:题目中所给的六边形,是一个不对称的图形,处理起来就比较复杂,不易发现已知量和未知量之间的联系。如果把它化为一个对称图形,那么问题就容易解决了。能做到吗?
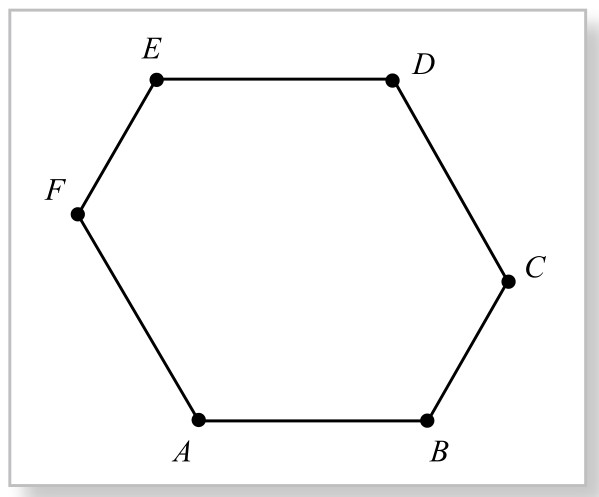
图2-6-8
我们来试一试。
这虽然是一个不规则图形,但其中有规则的因素:它的六个内角都相等。根据多边形内角和定理,知道它每个内角都等于120°。于是我们有以下几种方法,来构造规则的对称图形。
方法1:如图2-6-9,将各边延长,构成一个正三角形PQR。如图设线段,则AQ=FQ=f, CR=BR=b, DP=EP=d,从而,PQ=d+e+f=QR=f+a+b=PR=d+b+c,于是,BC+DE=b+d=PR-c=(a+b+f )-c=(a+b)+( f-c)=11+3=14。
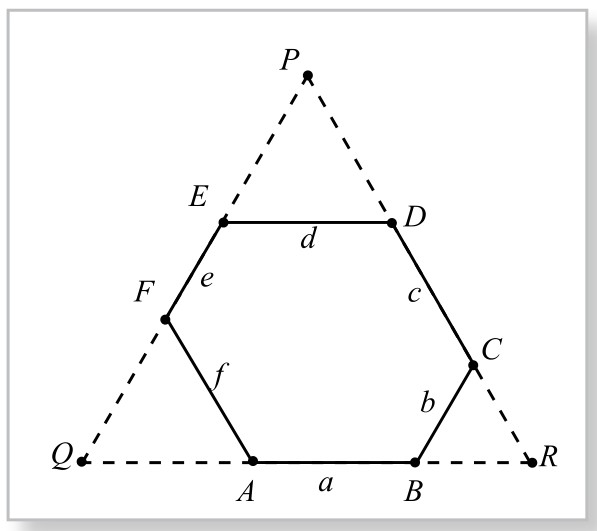
图2-6-9
方法2:如图2-6-10,延长BA, EF交于P,延长BC、ED交于Q。如图设线段构成平行四边形PBQE,则DC=CQ=DQ=c, AP=AF=PF=f,且a+f=c+d,故d-a=f-c=3,从而BC+DE=b+d=b+d-a+a=(a+b)+(d-a)=11+3=14。
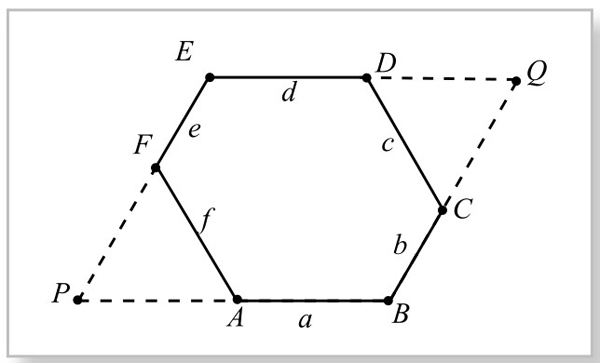
图2-6-10
以上证明的思想,就是将原来不规则的图形,补成规则的、对称的图形。此外,我们还可以将它补成其他类型的对称图形,如长方形、等腰梯形等。大家可以试一试。
(二)非对称几何曲线
例如,射线、不等边三角形、非等腰梯形、任意四边形、任意多边形、阿基米德螺线、对数螺线等,都是非对称图形。它们各自都有优美之处,表现之一,便是非对称的奇异美。尤其是在造型上,无论是在自然界,还是在现代建筑的体现上,都是另类“怪物”。它们突破常规,打破传统,另辟蹊径。
如自然界中许多奇异的生物,其外表奇形怪状,具有非对称的奇异之美。再如,世界著名的悉尼歌剧院(图2-6-11),其外形为曲顶蛙形,且大小、高低不同,独具魅力。而其最大的妙处是,建筑内部的聚音效果特别好,能够使任一座位上的观众,都能够清晰地听到舞台中央的歌声,回声、杂音干扰都减到最小。我国2020年通过竣工验收工作的雅西高速公路(图2-6-12),穿行在高山峡谷之间,被称为云中天路。重庆市区路网(图2-6-13),则纵横交错,多层立交重叠,充分展现了曲线之美。这些建筑都包含精妙数学思维和高超数学技术,都是数学美外化为形式美的体现。

图2-6-11 悉尼歌剧院外形

图2-6-12 雅西高速公路——天路雄姿

图2-6-13 重庆市区高架立交桥之美丽风景
