二、勾股与测天
二、勾股与测天
勾股定理,被认为是数学史上的第一定理,是人类智慧的结晶。但是,它在东西方数学发展史上的作用和地位,却大不相同。在中国古代,勾股定理是归纳的结果,来源于古人出于某种目的进行实际测量(例如测量日影长短,以制定历法;测量地势高低,以疏导洪水)的实际活动。而在古希腊,勾股定理则是演绎推理的结果,来源于几何理论。
相传距今约4000年的黄河流域,洪水泛滥,大禹为治理洪水,采用疏导的方法。为测量地势,他右执规矩,左执准绳,走到哪里就量到哪里。这里所说的规矩、准绳,都是测量用的工具。特别是“矩”,是最重要的测量工具之一。
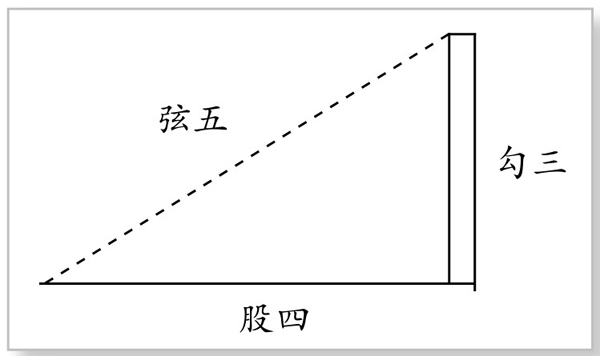
图4-2-1 勾三股四弦五图
矩可以用来画直角和垂线。矩不同于现在画图用的三角板,它是由两根木条制作而成,并构成直角的曲尺,没有斜边。如图4-2-1所示,将其中较短的边称为“勾”,较长的边则称为“股”。只有当这两边构成直角时,才能准确测量高低远近。如果不垂直,那么用其来测量,便会差之毫厘,失之千里。那么怎样才能保证“勾”与“股”这两边构成直角呢?这是个非常困难的问题。
我们的祖先在多次试验和实践,经过无数次失败之后,终于发现了“勾三、股四、弦五”的定理!即取勾长为三单位,股长为四单位,若能用一根五单位长的线恰好连接勾股两边的端点成一直线“弦”,那么,这勾与股两条边,就一定垂直。由此定理(实际上是勾股定理的逆定理),便能够很方便地制作出标准的测量工具——矩。这真是个了不起的发现!
大家不要以为“勾三、股四、弦五”只不过是勾股定理的特例,并不能算是发现了勾股定理。其实,这是勾股定理最重要的特例。而且这是中国古代劳动群众,在长期劳动实践中的伟大创造。人们利用这一发现,才能判定和制作出两边垂直的矩,也只有用这样标准的矩,才能进行准确的测量。我们可以这样合情推理:人们正是从这简单的特例,逐步发现勾股定理的一般情形。而反过来,若直接用勾股定理的一般情形,是制作不出两边垂直之矩的。
中国古代的先贤们,不仅利用勾股定理(及其逆定理)制作标准的测量工具——矩,而且巧妙地利用矩或联合利用两个矩,进行各种复杂的高低远近的测量工作。其中以祖冲之进行日影测量,制定历法,最为精妙。(以下可参阅书末参考文献[12]P33-37)
中国自古以来就是“以农立国”,而农业对气候的依赖性极大。人们发现,一年的气候变化似乎与太阳的位置有关。在一年之中,日影长短是周期性变化的,与气候的寒暑交替的规律一致:中国位于北半球,在太阳底下立一根木桩,一年之中有一天木桩的日影最长,这一天被人们称为“冬至”;有一天木桩的日影最短,这一天被称为“夏至”。因为日影长时更容易测量,故把冬至这一天定为一年(回归年)的开始。那么如何才能准确地测量出日影的长度呢?首先要保证的便是木桩与地面垂直,这样测量出的日影才是准确的。
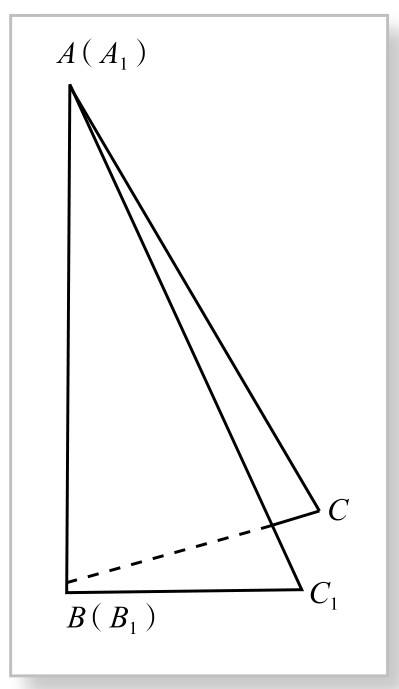
图4-2-2
要将木桩垂直于地面,抽象来看,就是要使一条直线垂直于一个平面。那么,我们应该怎么办呢?在远古时期,中国的先民们就发现如下用矩之道:将大小相同的两个矩的短边(勾)放在平地上,将两个矩的长边(股)合在一起,若能重合成一条线段,那么,这重合的股边,便垂直地面。如图4-2-2所示。实际上,这相当于一条立体几何公理:若一条直线垂直于平面上两条相交直线,则该直线与平面垂直。
历法,是年、月、日和节气安排的时刻表。但是,时间无头无尾,瞬息即变,人们是如何测定和记录它的呢?古人发现,将一根圭表(测量日影长短的标杆)竖直立于地上,一天之中它在正午时刻的影子长度最短,而在一年的不同季节里正午日影长度又是不同的:冬至最长,然后逐渐缩短;夏至最短,然后又逐渐增长。在一年之中,周而复始。
因为影子长时容易测量,故测量冬至点的日影长度,以确定一个回归年的开始时刻,就成了天文历法的重要工作。
但是,仅凭测量圭表正午影长来定冬至点的做法,是不准确的。原因是:
第一,这只能确定哪一天正午的圭表日影最长,不能确定冬至点所在的时刻。而一般说来,冬至点并不正好在正午。事实上,一年大约有365+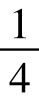 日,如果第一年冬至点在正午,第二年就应在傍晚,第三年在半夜,第四年在早晨。所以,即使冬至点有可能在某年的正午,也要连续进行四年测量,才能确定。
日,如果第一年冬至点在正午,第二年就应在傍晚,第三年在半夜,第四年在早晨。所以,即使冬至点有可能在某年的正午,也要连续进行四年测量,才能确定。
第二,只能在冬至日附近连续多天天气晴好时测量才行。如果遇到天气不好——下雨、下雪,或者阴天,都无法进行日影测量。那么,又要重新开始,再进行连续四年的测量。
因此,这种方法是不可能测准冬至点的。在祖冲之之前,冬至点的确定,虽然有测量数据为依据,但实际上不是测量出来的,而是估计出来的。
冬至点的测量(估计)误差,必然造成回归年长度的误差。即使每年只差0.1日,过了50年,积累误差也会相当大——一年就要相差5日。到了这时,这部历法就不再能反映季节的变化,更不能预报日食、月食等天文现象,那么就要改历了。所以,如何准确地测量冬至点,就成了历代天文学家、数学家关注的大问题。
祖冲之为了制定新的历法,运用数学智慧,创造了科学的新方法,解决了这个难题。具体做法如下:他于(南朝)刘宋大明五年(461年)冬至前后的一个半月内,选了三个晴天,进行了三次正午的日影长度的测量,具体数据见《宋书·历志》,记载如下(日期为农历):
10月10日(A)——影长10.7750尺(a);
11月25日(B)——影长10.8175尺(b);
11月26日(C)——影长10.7508尺(c)。(https://www.daowen.com)
为简化计算,他做了如下合理假设:
(1)在冬至前后日影关于冬至点是对称的;
(2)在一天之内,日影变化是线性的,即它与时间成比例。
如图4-2-3所示,设冬至点为Y, A关于Y的对称点为X;AB的中点为M,则
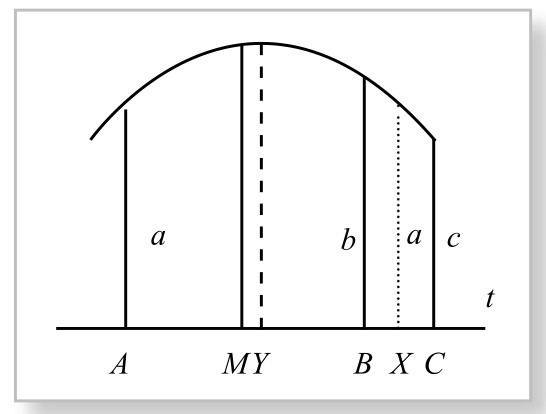
图4-2-3
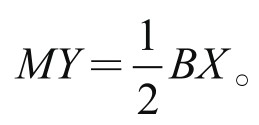
由假设(1),因为b>a>c,所以A点关于冬至点Y的对称点X,应在B点与C点之间。
我们注意到:B点到C点,正好是一整天,再由假设(2),则应有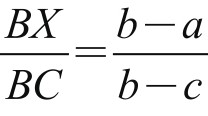 或
或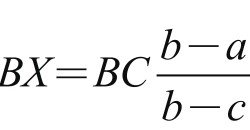 。
。
根据我国古代计时制度,一天分为100刻。
于是将BC=100,及a、b、c数据代入公式得
BX=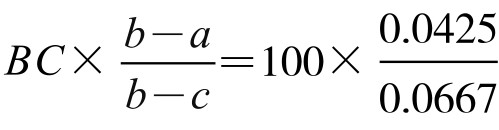 ≈64(刻), MY=
≈64(刻), MY=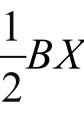 =32(刻)。
=32(刻)。
因为M点是(农历)十一月初三日午夜零时,故这一年的冬至点是十一月初三日午夜零时后32刻。换成现在的时间,这年的冬至点大约相当于这一天早晨7时41分。
祖冲之测量冬至点的数学智慧表现在以下三个方面:
首先,他的两个假设是合理的、科学的,符合实际情况。这样,就使原来单靠经验和估计来测算冬至点的传统方法,建立在数学理论基础之上,成为科学的测算方法。
其次,方法简单易行。它使冬至点的测算不受天气影响,且大大缩短了测算时间:从四年或更长时间,缩短到可在一年之内完成。实际测量时,只需要在冬至前后大致对称的时段里,分别测算几天正午的日影长度;然后选取三个数值a、b、c(其中有两天是连续的),使b>a>c,即可。
最后,可以大大提高测量的精确度。传统冬至点测量方法,只能精确到1天以内,而祖冲之的测算法,则可以精确到1刻以内(1刻=24×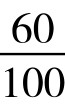 =14.4分钟)。
=14.4分钟)。
正因为如此,祖冲之首创的冬至点测算法,一直为以后历代历算家所尊崇和采用。
由于祖冲之对冬至点的测算精确可靠,所以他据此制定的历法——《大明历》所定的年、月、闰周的数值,都达到了前所未有的精确度:
(1)1回归年=365.24281481日。
与实际情况相比,1000年才多半日,其精确度在当时世界上遥遥领先;在中国,直到南宋《统天历》(1199年)才被超过。
(2)1朔望月=29.5305915日。
与实际情况相比,每月误差不到0.5秒,领先世界500多年;直到北宋《明天历》(1064年)才有更好的结果。
