数学是运动的艺术
三、数学是运动的艺术
远古时期的人们,虽然没有科学知识,但是他们能通过眼、耳、鼻、舌、皮肤等人体器官接触外界,可以观察和感知到天地万物在不停地运动:天空中的风雨雷电,夜晚的月亮和星辰闪烁,冷暖寒暑的周期变化,花开花落,四季更迭,如此等等。
当然,古人最易感知的是天地形状和季节变化。因为这与人类的生存关系最大。天高难问,只能想象。中国的先民们最初的想象是“天圆地方”,即所谓“盖天说”。古人吟唱道:“天似穹庐,笼盖四野。”形状为圆的天,怎么能盖住四方形的大地呢?有人解释道:盖不住的大地四角,是大海。大海太远,无人能到。于是又出现“浑天说”和“宣夜说”。但都因不能自圆其说而不了了之。
西方古哲人对天地观测,不仅注意记录和总结,而且善于思考和推理。古希腊托勒密提出了“地心说”的宇宙模式,认为日月星辰,都以地球为中心,在各自不同的圆形轨道上周而复始地运行。直到16世纪,哥白尼提出“日心说”,而后伽利略、第谷和开普勒等,通过多年对天文观测数据的分析总结,论证了“地心说”的错误。实际上,包括地球在内的各个行星,都以太阳为中心,在各自的椭圆轨道上运动,而太阳则在椭圆的一个焦点上。“日心说”科学地解释了地球上人们所感到的四季更迭、天上星座周期变化的规律。17世纪,牛顿更进一步,运用新发明的微积分理论,著《自然哲学的数学原理》(1687年),在前人工作的基础上,提出万有引力公式,将天体运行的规律,建立在严密的数学理论基础之上。
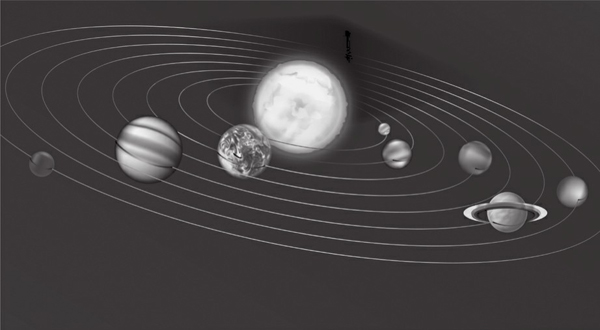
图2-3-1 太阳系行星运行轨道略图
如果说音乐是听觉的艺术,绘画是视觉的艺术,那么数学就是一切运动的艺术。没有什么运动,不能用数学公式进行表述和描述。在数学家眼里,数学符号和数学公式,就是关于天地万物运动的艺术。
试看地球公转运动:
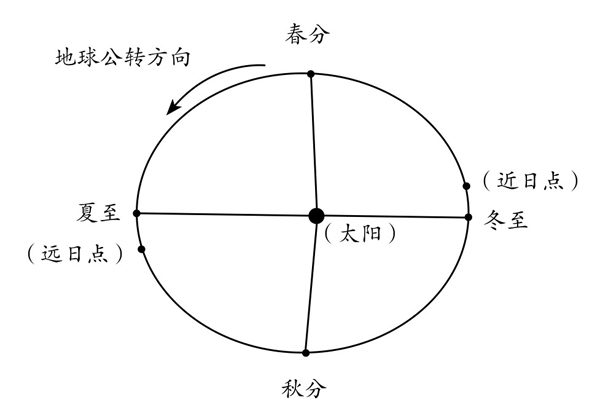
图2-3-2 地球绕太阳公转图
地球在一个近似于圆的椭圆轨道上运动,太阳在椭圆的一个焦点上(如图2-3-2)。通过精确计算,我们可以知道地球椭圆轨道的长、短半轴及两个焦点的位置。于是就可以知道地球与太阳的远距离数据、近距离数据,以及地球的运行速度。根据开普勒第二定律,太阳与地球的连线扫过的面积与时间成正比,而连线每扫过15°为一个节气,所以在近日点附近的两个节气之间的时间较短,而在远日点附近的两个节气之间的时间较长。通过计算,便可以确定地球一个回归年的时间长度、每个季节的节点时间。对于中国传统的阴阳合历的历法制度而言,还有设置闰月、确定二十四节气时刻等,结果都可以准确地被计算出来。
如此远大无边的天地万物,都可以运用数学公式加以精确计算,真是令人惊叹不已,多么伟大的艺术啊!数学家的数学艺术,难道比艺术家的艺术逊色吗?
公式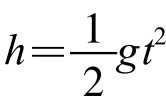 ,描述了物体在只受重力作用下自由落体的距离与时间的关系,其中g为重力加速度,在一般中低纬度地区,其值定为9.80米/秒2。
,描述了物体在只受重力作用下自由落体的距离与时间的关系,其中g为重力加速度,在一般中低纬度地区,其值定为9.80米/秒2。
又如速降线数学公式,刻画出了一个有质量的物体最快降速所经过的运动轨迹。悬链线数学公式,则描述了一个质量均匀的绳索,在自然悬挂情况下的形态。
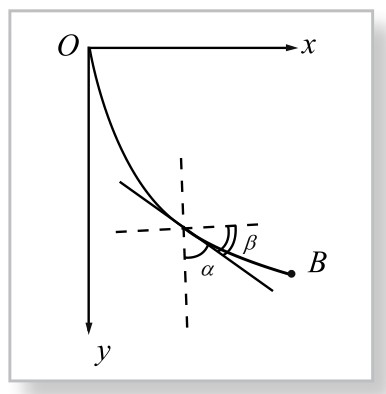
图2-3-3 速降线
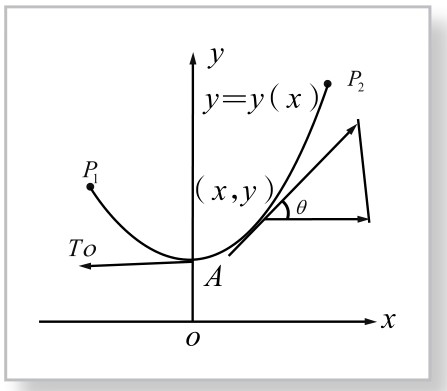
图2-3-4 悬链线
即使是现代数学,如群论、非欧几何、拓扑学、分维度几何等,也是现实世界中各种对称运动、混沌运动和大宇宙空间运动的反映,及对其进行研究的工具。
