哈代与色盲遗传之困
五、哈代与色盲遗传之困
(一)一个惊人的难题
色盲,虽然不是什么严重的疾病,但它是人的一种先天性视觉障碍。大约在20世纪初,有人发现色盲是可以遗传的。于是提出了一个惊人的问题:色盲既然能遗传给下一代,那么,将来会不会全世界的人都成为色盲?眼睛是人体十分复杂的器官,色盲又与遗传因素有关。当时,人们还不了解遗传基因的结构,根本没法了解色盲在遗传基因上的原因。所以,这似乎是当时无法解决的难题。
这个问题被提到了哈代那里。哈代(1877—1947)是英国大数学家,自称是纯粹数学家,对实际问题不感兴趣。但是,这回可是个例外。他对这个问题不但有兴趣,而且从概率统计的观点出发,仅用初等代数知识,就巧妙地解决了这个难题。请看他的奇思妙想。

图4-5-1 哈代
(二)哈代的分析
他分析了大量临床统计资料,得知以下情况:
1.色盲者中,男女都有,但男性患者比女性患者多得多;
2.父亲色盲、母亲正常,其子女不色盲;
3母亲色盲、父亲正常,其子女中男孩色盲、女孩正常。
因此,他判断:色盲的遗传与性别有关。当时人们知道的情况是:男女性别的差异,与遗传基因中的性染色体有关。每个人的体内有23对染色体,每对染色体中的2条染色体形态基本相同,分别来自父亲和母亲;其中有一对特殊的染色体——性染色体,决定人的性别。男性的性染色体是XY,女性的性染色体是XX。在遗传给下一代时,母亲赋予子女的总是X,父亲随机地给予子女X或者Y,所以男女出生的概率是1∶1。
既然色盲与性别有关,所以色盲者一定是性染色体上出了“毛病”。那么,究竟是X出了“毛病”,还是Y出了“毛病”呢?——一定是X,而且这条“异常”染色体会世代遗传下去。
为什么能肯定“异常”染色体是X呢?这可用反证法来证明:假如“异常”染色体是Y,女性就不会有色盲,因为女性染色体中没有Y。但是,有女性色盲存在,只是比男性色盲少而已。所以“异常”的一定是X,而不是Y。
那么,为什么男性色盲比女性多呢?这是因为女性有两个X,如果其中有一个异常、一个正常,仍然可以维持正常。我们暂称此为“次正常”(非色盲)。
这样,男性就分为两类:正常和色盲。女性则分为三类:正常、次正常和色盲。
根据这些分析,就可以利用数学方法,来估计下一代人中的色盲比例。
为了方便数学处理,哈代作了如下合理假设:
其一,在两类男子和三类女子之间,夫妇配对的机会是随机的。
其二,“异常”染色体(记作“X-”)在所有染色体中所占比例p,在男、女染色体X中的比例也保持不变。
其三,子女中男女出生比例为1∶1。
(三)建立数学模型和计算
男性中正常和色盲两类,以F、S表示;女性中正常、次正常和色盲三类,分别以Z、C、K表示。则F、S在男性中所占比例分别为q、p(q=1-p);Z、C、K在女性中的比例,分别为q2、2pq(因为女性有两个X ,可以任选一个)、p2。因此,男女色盲数占总人口数的比例为: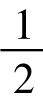 (p+p2)。
(p+p2)。
夫妇配对有6种类型,在夫妇总体中各占比例如下:
第一类(F, Z)——男、女均正常,q3;
第二类(F, C)——男正常、女次正常,2pq2;(https://www.daowen.com)
第三类(F, K)——男正常、女色盲,p2q;
第四类(S, Z)——男色盲、女正常,pq2;
第五类(S, C)——男色盲、女次正常,2p2q;
第六类(S, K)——男女均色盲,p3。
以下分类计算这6类夫妇的子女中色盲的概率。
第一类夫妇,显然子女中不会有色盲。
第二类夫妇(F, C)子女的染色体搭配有4种情况,如表4-5-1所示:
表4-5-1
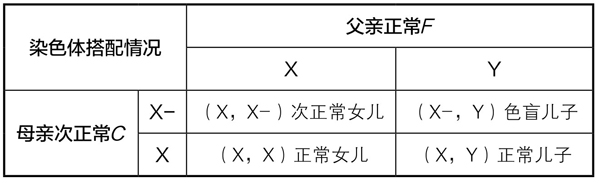
4种情况中有1种是色盲,即这类夫妇的子女中有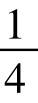 是色盲,在下一代人口中所占的比例是2pq2×
是色盲,在下一代人口中所占的比例是2pq2× 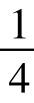 =
=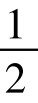 pq2。
pq2。
第三类夫妇(F, K)子女的染色体搭配也有4种情况(表4-5-2):
表4-5-2
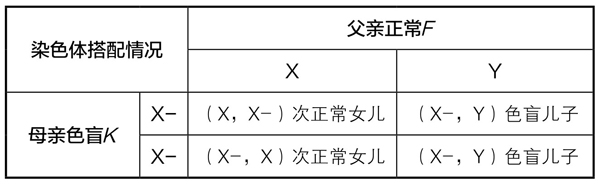
4种情况中有2种是色盲,故这类夫妇的子女中有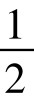 是色盲,在下一代人口中所占的比例是
是色盲,在下一代人口中所占的比例是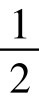 p2q。
p2q。
第四类夫妇(S, Z)子女的染色体搭配也有4种情况(表4-5-3):
表4-5-3
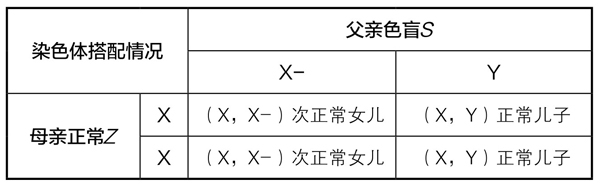
此类夫妇的子女不会有色盲。
第五类夫妇(S, C)子女的染色体搭配也有4种情况(表4-5-4):
表4-5-4
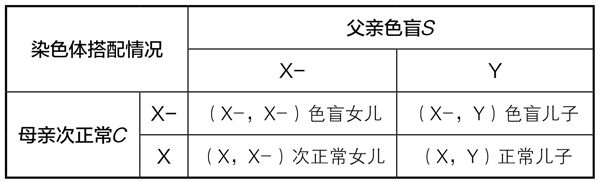
这类夫妇的子女中有一半是色盲,在下一代人口中所占的比例是2p2q× 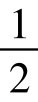 =p2q。
=p2q。
第六类(S, K)的子女,显然一定是色盲,其在下一代人口中占p3。
将以上6类(实际只有4类有色盲子女)夫妇的子女中色盲的比例数相加得:
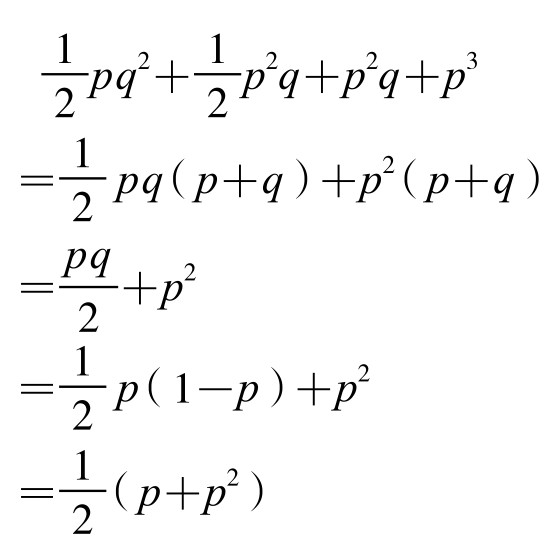
此即下一代人口中色盲所占的比例。
(四)结论
我们惊奇地发现:它与上一代人(即父母辈)中色盲所占比例完全相同!
由此可以得出结论:色盲虽然会遗传给后代,且随着总人口的增加,色盲的绝对数量会增加。但是,色盲在每代人中所占的比例不会增大。所以,绝对不会使全人类都变成色盲!
到此,面对这个惊人的难题,哈代运用他的数学智慧,仅用简单的中学数学知识,就巧妙地解决了。这不能不令人惊叹,惊叹数学之大用,数学之大美!
