从河图洛书到完美幻方
相传,我国远古伏羲时代,黄河有龙马负图出水,是谓“河图”。大禹治水时,洛水又有老龟负书出水,是谓“洛书”。其实“河图”“洛书”(如图5-1-1、5-1-2所示)都是由点数排列而成的。
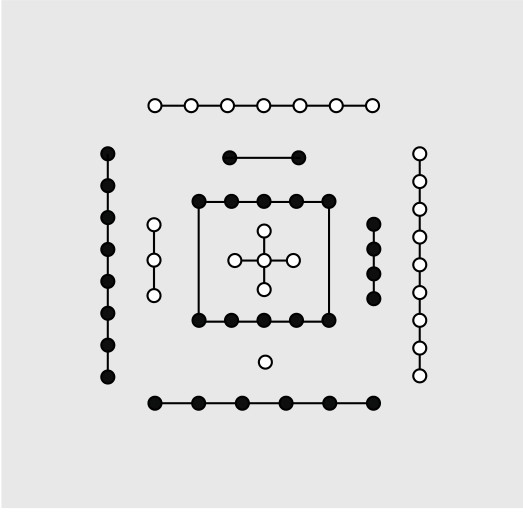
图5-1-1 河图
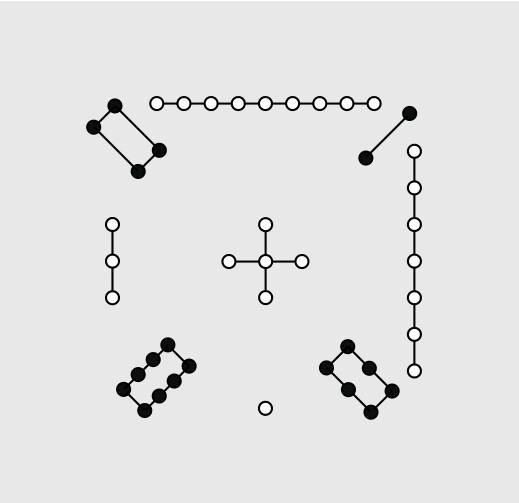
图5-1-2 洛书
如果以数字代替点数,则变为由1, 2, 3, …, 9这九个数字排列而成。其中“洛书”则成为如图5-1-3所示的数字图阵。但这不是一个随便做出的数字图,其中数字排列大有讲究:它的每行、每列三个数之和,都是15。而且两条对角线上三个数字之和,也是15。这就绝不是自然之物,而是人类精妙的思维结晶。
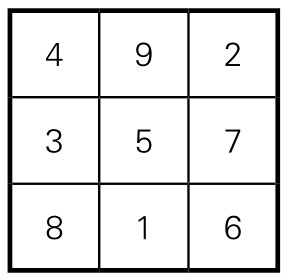
图5-1-3
类似这样的数字方阵,中国古代称之为“纵横图”,西方则称之为“幻方”。
上述数字图5-1-3,中国古代称为九宫,现在称为三阶幻方。13世纪,中国数学家杨辉将三阶纵横图(幻方),推广到四阶、五阶方阵,以至于其他形式的连环图。如图5-1-4所示的“四四图”,每行每列四个数字之和(称为幻和)都等于34;“五五图”(图5-1-5)的幻和等于65。他还研究出幻方的编制方法。
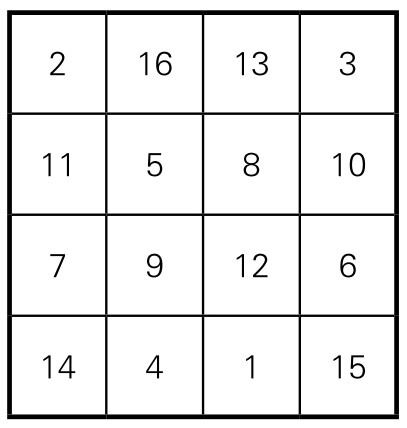
图5-1-4
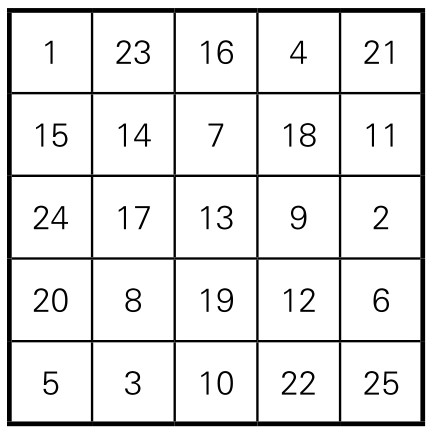
图5-1-5
(一)完美幻方向宇宙昭示地球人的智慧
幻方,以其巨大的、奇妙的魔力,吸引着许多人的兴趣。世界各国研究者、业余爱好者,经过不懈的努力,不断有所发现,有所创造,并且把幻方应用到生产实验设计、网络设计等方面。
20世纪后半期,当人类把人造卫星发射上天,开启航天时代以后,便想到宇宙外星人的存在,以及如何与之建立联系的问题。
宇宙空间之大,远非地球人所能想象到的。宇宙除了地球有生命存在以外,很可能还存在其他星球有类似地球人的生命形态,即外星人的存在。这并非异想天开。如果真有这样的天体存在,其上有智慧生物,我们地球人应如何去与他们打招呼和联系呢?——写信?不行。因为彼此语言不通。
——发电报?不行。因为信息的密码不同。有什么好办法呢?
我们或许可以用图画来表达地球人的面貌和情况。但如何反映地球人的聪明才智呢?当时我国数学家华罗庚提出一个绝妙的想法:用点子表示数目,画一个四阶完美幻方,即如图5-1-6所示。如果把图中的点子数目,换成数字,它便是如图5-1-7所示的四阶数字幻方。

图5-1-6智慧的完美幻方
为什么把它叫作“完美幻方”呢?因为它实在太完美了!我们来说说它的奥妙:
1.它首先是一个幻方,具有幻方的所有性质。它每行、每列和两条主对角线数字之和都等于34。
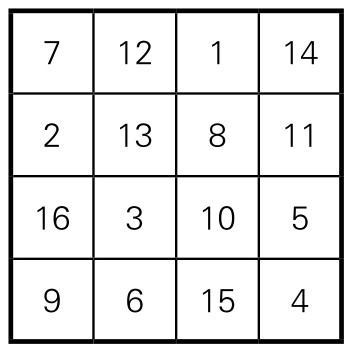
图5-1-7
2.若把两个幻方并起来,如图5-1-8,除了两条主对角线(用实线表示)外,还有六条斜对角线(左右各三条,用虚线表示),其上的数字之和也是34。
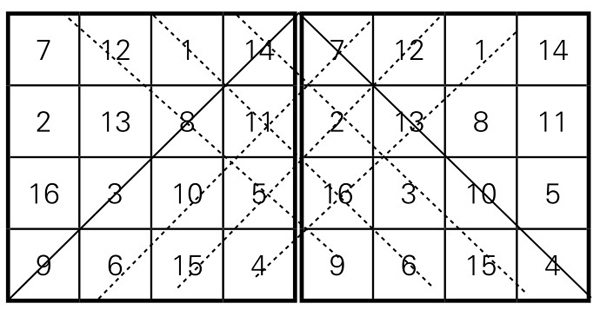
图5-1-8
3.四个角上的四个数字之和也是34。
4.对边中间两个数字和也是34。
5.中间的四个数字和也是34。
6.用中心线把它分为四块,每块的四个数字和也是34!
真是太完美了!如果要用一个字来形容它的“美”,那就是——妙!实在太妙了。
这真是数学之大美,人类智慧之奇妙!
所以,将此完美幻方带上卫星,发射到外太空,可以向外星人告知地球人智慧的发展高度,以其作为彼此沟通的信使,是很恰当的。
(二)幻方的两种简单构造法(https://www.daowen.com)
幻方神奇,一般人要想编制一个五阶幻方,若不知道窍门,那确实很难。
经过历代中外幻方爱好者的努力钻研,现在已找到多种幻方的编制方法。在此介绍两种奇数阶(不限于五阶)幻方的编制方法。
1.顺序斜排法
以五阶幻方为例,来加以说明。
先将五阶方阵,扩充至九阶方阵。
第一步,在中间的内接菱形的格子里(包括边线上的格子),从左边中间一格起,在菱形的格子里,依次写入1, 2, 3, …, 25,如图5-1-9。
第二步,将中间菱形格子以外的小格擦去,如图5-1-10。
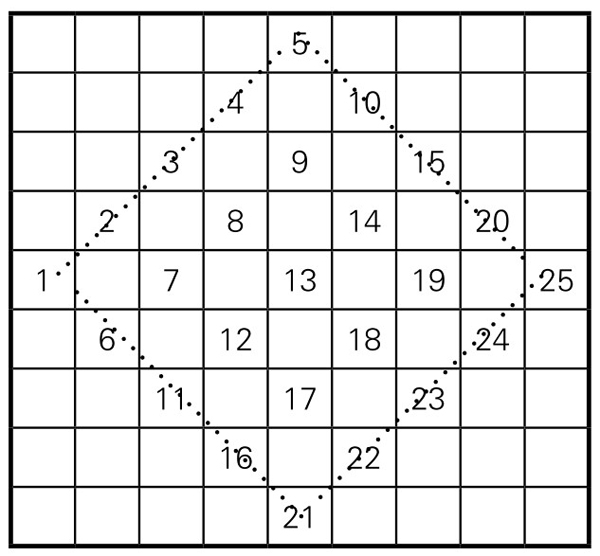
图5-1-9
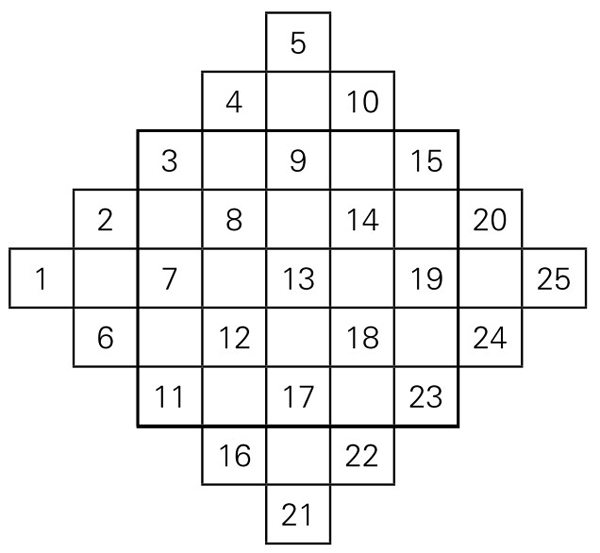
图5-1-10
第三步,中间五阶正方形数字图阵保持不动,将四边外的“品”字形格子剪下来,如图5-1-11的四个小图。
第四步,将这四个小图对换位置(左右对换,上下对换),并将其中的数字,按照相应的顺序,填入到大图的空格中,如图5-1-12。这样便完成了一个五阶幻方的编制,如图5-1-13。
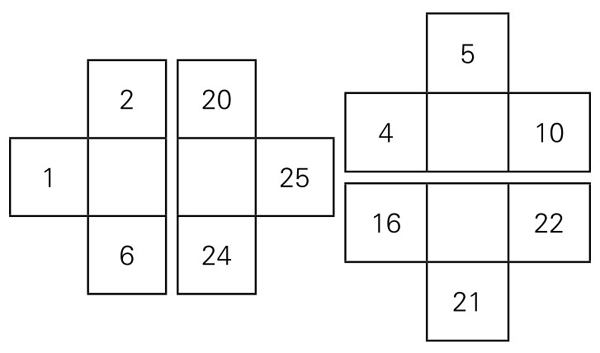
图5-1-11
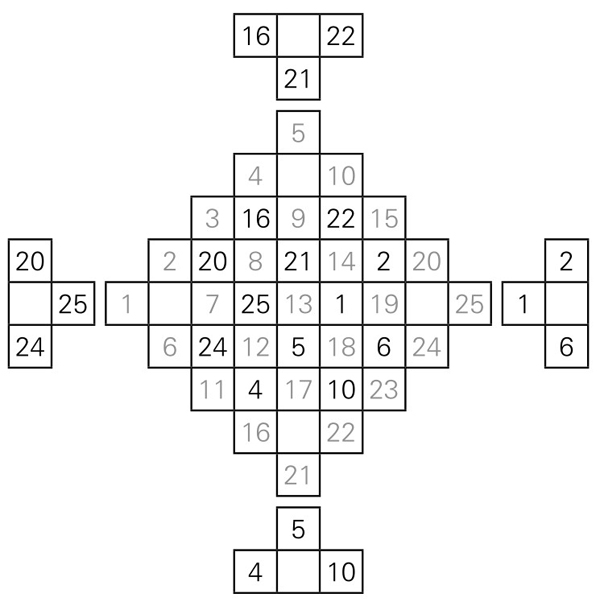
图5-1-12
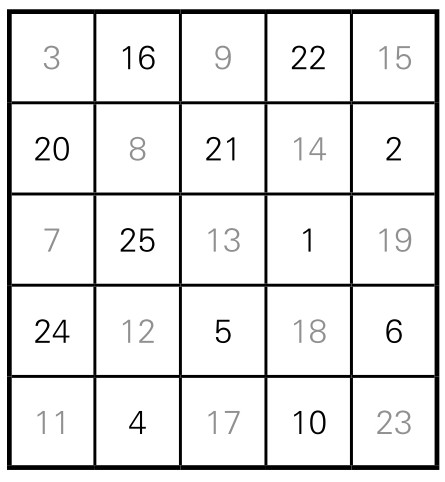
图5-1-13
大家可以通过计算,验证它确实是一个符合条件的五阶幻方。
2.双偶数阶对称填数法
对于双偶数(即形如n=4m的偶数),有个方便的幻方编制法。现以八(8=4×2)阶幻方为例来说明。
第一步,因为8是4的倍数,可以用横竖中心线把八阶方阵分为4个相等的四阶小方阵。
第二步,在左上的一个四阶小方阵的每行上,任意取两个格子画个小圆圈“○”,共画8个。
第三步,将此画过圆圈的小方阵,上下、左右对称地反射到其他三个四阶小方阵上。这样整个八阶方阵上的小圆圈有32个,正好占据一半格子,而另一半为空格。
第四步,从左上角第一格开始,依次写数字1, 2, 3, ……直到64。但凡是有“○”处,跳过去不写。如图5-1-14,图上有一半格子填入了数字,一半格子是圆圈。
第五步,从方阵的右下角开始,再依次填写1, 2, 3, ……直到64。不过,跳过已经填有数字的格子,仅在“○”处填数字。这样做的结果如图5-1-15, 64格都填上了数字,且64个数字不重复。这样填出的方阵,就是一个八阶幻方。
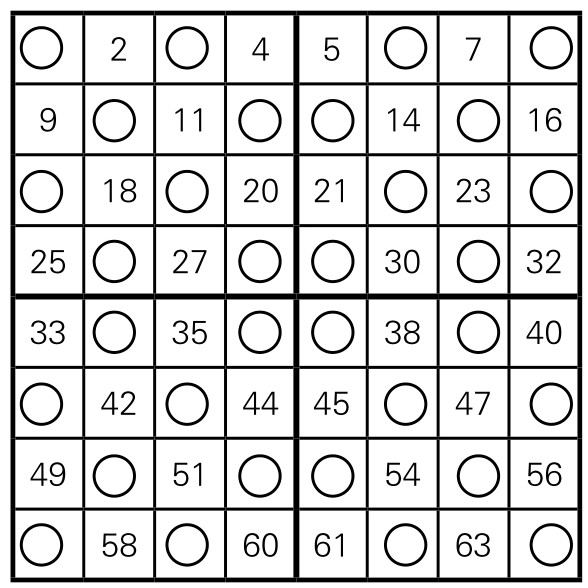
图5-1-14
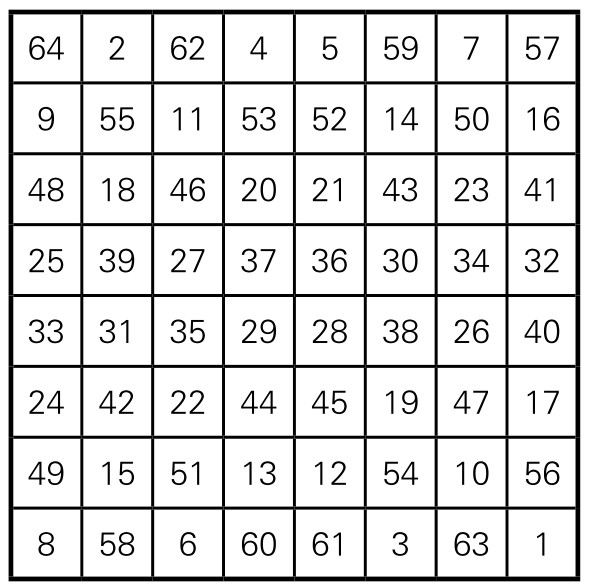
图5-1-15
如果在开始时,换一种方式填入小圆圈,其他步骤照做,那么,我们会得到一个新的八阶幻方。可见,同一阶幻方不止一种,而是有很多种。至于究竟有多少种,这又是另一个复杂的数学问题。
幻方诞生在中国,后来才传入西方。但是现在世界各地,都有不少幻方的研究者和爱好者。有世界性的幻方组织、幻方协会、幻方刊物。中国也有很多幻方研究者和爱好者,成立了“中国幻方协会”,并出版杂志《中国幻方》。我国还有研究者创造过不少新的幻方。如安徽芜湖市的杨弋,在他年仅六岁时,就因巧解“八阶双重幻方”的最小和,而获得了中央四部委授予的“21世纪之星”称号(百名之一)。他还创制出了十阶完美幻方(图5-1-16)。
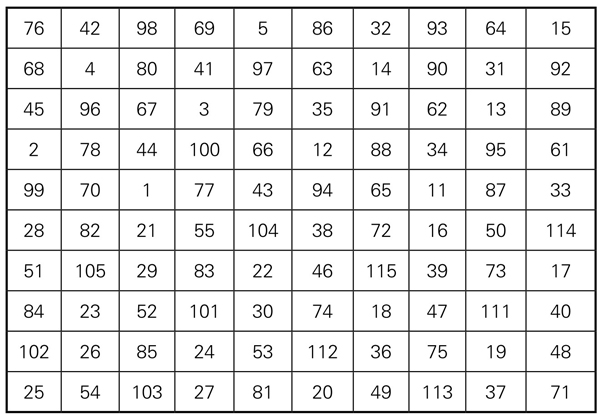
图5-1-16 杨弋编创(非典型)十阶完美幻方
面对如此精彩绝伦的完美幻方,我们能作何评价呢?只能用一个字——“妙”!
