从拣石子游戏探究怪题奇解

二、从拣石子游戏探究怪题奇解

（一）问题的缘起

刊载于1978年8月19日《参考消息》上的IMO-20试题印刷上的错误，使得其中第三题十分难解。全国各地掀起了一股研讨该题的热潮，从中学数学教师到大学数学教授，都从不同思路，用不同方法给出自己的解答，印出过多种解答材料。其中张国铮先生的正确解答发表最早。早在《中学数学教学》创刊之前，安徽师范大学数学系和函授部合编的《数学函授教学》就发表了张国铮先生给出的解答。后来，又是张老最先将龚升教授从美国寄来的IMO-20英文试题和解答翻译成汉语，在《数学函授教学》1979年第二期上发表，成为国内关于IMO-20试题解答的最早正确文献。

刊登在1978年8月19日《参考消息》上的I M O-20试题第三题：

设f, g:Z+→Z+严格递增函数，且f（Z+）∪g（Z+）=Z+, f（Z+）∩g（Z+）=Ø, g（n）=f（f（n））+1，求f（2ω）。这里Z+是正整数集合，Ø是空集。（8分，英国）

其中最后结论“求f（2ω）”是“求f（240）”的误写。但是这个错误，使一个函数求值的计算题，变成了求函数f（n）一般函数表达式的问题。其难度大大提高，对于一般中学数学教师，乃至于大学数学教授而言，都是个大难题。因为这两个函数的表达式十分古怪：

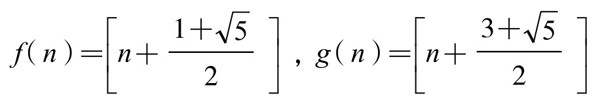
求其表达式，已超过中学生和大学生的数学水平。要求出这样的函数表达式，相当困难。安徽师范大学数学系当时的副主任张国铮先生，从数学家闵嗣鹤发表在《中国数学杂志》（《数学通报》前身）1951年第二期的《由拣石子得到的定理》一文中，得到启发，找到了它的第一个解答，并发表在1979年初出刊的安徽师范大学主编的《数学函授教学》上。

（二）二人玩的“拣石子”游戏

随意放两堆石子，甲乙二人轮流从中拣取，游戏规则如下：

1．二人轮流取，轮到谁取，必须取，不可以不取。

2．可以只从一堆中取，也可以同时从两堆中取。若只从一堆中取，随便取多少个（至少一个）；若同时从两堆中取，也随便取多少个，但两堆要取一样多。

3．最后完全取光者为胜。

此游戏若有人知道诀窍，则先取者必胜。该诀窍是给对方留下“先输组”:（1, 2）（3, 5）（4, 7）（6，10）（8，13）（9，15）（11, 18）……（f（n）, g（n））……

前20个“先输组”如表5-2-1所列：

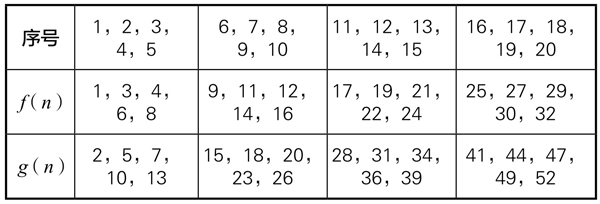
譬如，甲给乙留下了（1, 2），按规则，乙无法一次拿光。乙取后，留给甲的有四种可能：（0, 2）（1，1）（1, 0）（0，1）。于是，按规则，甲都可以一次拿光而得胜。

又如，甲给乙留下（3, 5），那么乙取后留给甲的，有11种可能：（0, 5）（1, 5）（2, 5）（3, 4）（3, 3）（3, 2）（3，1）（3, 0）（2, 4）（1, 3）（0, 2）。

于是，甲相应地应该给乙留下（0, 0）（1, 2）（2，1）（1, 2）（0, 0）（2，1）（2，1）（0,0）（2，1）（1, 2）（0,0）。就是说，或者甲直接获胜，或者留给乙“先输组”（2，1）或（1, 2），最后还是甲获胜。

若两人都知道诀窍，那么，只要一开始两堆石子数目不是“先输组”，那么谁先取谁获胜。

假定开始时两堆石子数是（a, b），又若a＜b（a=b则可以一次拿光得胜），且（a, b）不是先输组。

（1）若a等于某个f（n）, b＞g（n），或等于某个g（n），那么都可以通过减少b或a，而给对方留下“先输组”（f（n）, g（n））。

（2）若a等于某个f（n），而b＜某个g（n），设b-a=n′＜n，

则n′=b-a＜n=g（n）-f（n）（这是函数f（n）、g（n）的性质）。

因为g（n′）-f（n′）=n′=b-a，所以a＜a-f（n′）=b-g（n′），这个共同的差数，记为k（正整数）。这时，只要两边同取k个石子，留下的就是“先输组”:（f（n′）, g（n′））。

（3）函数f（n）, g（n）性质（证明略）。

令f（n）的值域F={f（n）}, g（n）的值域G={g（n）}，则有：

1. f（n）与g（n）皆严格递增；

2. F∪G=Z+, F∩G=Ø；

3. g（n）=f（n）+n；

4. g（n）=f（f（n））+1。

因为F∪G=Z+, F∩G=Ø，即函数f（n）、g（n）的值域之和，恰好完全覆盖了整个正整数集。故若（a, b）不是“先输组”,（1）（2）包括了所有情况。

这个游戏中的两个函数f（n）, g（n）恰好就是IMO-20届第三题中的那个形式古怪的函数。

所以按照《参考消息》上错误印刷的问题，其答案就是

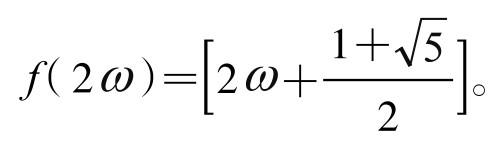
其实题目的原意只是求函数f（n）的一个值f（240）。用函数（f n）的一般表达式，反而不好计算。需要用该函数的性质g（n）=f（n）+n才方便计算。

1978年8月19日的《参考消息》之所以发生这样不该发生的错误，据说是因为当年IMO-20届数学竞赛在罗马尼亚首都布加勒斯特举行，当时正好有一个科技方面的中国代表团在该市访问。团员中有个数学爱好者，对此颇感兴趣，便在匆忙中将试题抄写下来，由于抄写的字迹潦草，把其中的结论“求f（240）”中的240写成2ω。而《参考消息》的编辑也没有认真核对，就很快见报了。无意中引发了一场不大不小的数学界“风波”。

本书作者之一胡炳生，当时也是研究此题解答的当事人。他求出了函数f（n）的一种递推表达式：

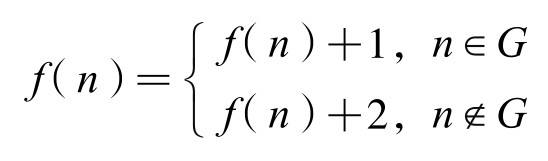
根据上述递推公式，从f（1）=1开始，便可以依次写出函数f（n）的值，然后，在其空格处依次填上函数g（n）的值，就可以得出所有函数值。

鉴于求函数表达式的难度太大，作者（胡炳生）曾经大胆猜测：题目印刷可能有错，题目的要求也许不是求函数f（n）的一般表达式，而是求它的一个值，例如求f（200）。认为2ω可能是200的误写。虽然没猜准具体函数求值，但是对题目要求结论的方向，倒是猜对了。

由于1978年8月19日的《参考消息》对IMO-20试题的印刷错误，带给了中国数学界关于国际数学竞赛的热情，并由此而兴起，历久不衰。这样看起来，这个错误在无意中，也未必不是做了一件有意义的好事情。