由赌博问题引出的大学问
八、由赌博问题引出的大学问
(一)故事由来
在17世纪的法国,有个颇有文化素养的赌徒梅累,在赌博中遇到一个棘手的问题:得分问题。
先来说说当时欧洲赌博游戏的规则:一般是二人对博,双方各出同等赌资,放在一起作赌注,事先约定先得几分者为胜。每局胜者得1分,最后胜者获得全部赌资。梅累遇到的“得分问题”是:A、B二人各出金币32枚作赌注。约定先得4分者获胜,获得全部64枚金币。但是由于某种突发情况,在A得2分、B得1分的情况下,赌博终止。试问:这时应该按照什么比例来分配这64枚金币?
梅累虽然是一个熟练的赌徒,但是不能解决这个难题。于是他向法国天才数学家——帕斯卡(1623—1662)求教。而帕斯卡又把这个问题写信给他的朋友——被誉为“业余数学家之王”的费马(1601—1665)。
经过思考和研究,费马和帕斯卡从不同的思路上给出了各自的解法。
(二)费马的方法
费马的逐步排列法:设想赌局继续再进行4局,总可以得出最后结果。于是他列举出各种胜负可能情况,以计算各人的胜负可能性:
1.A胜4局,B全负,这只有一种情况——aaaa;

图5-8-1 费马
2.A胜3局,B胜1局,这有4种情况——aaab, aaba, abaa, baaa;
3.A胜2局,B胜2局,这有6种情况——aabb, abab, abba, baba, bbaa, baab;
4.A胜1局,B胜3局,这也有4种情况——bbba, babb, abbb, bbab;
5.B胜4局,A全负,这也只有一种情况——bbbb。
以上共有16种情况,其中有11种情况A胜;其余5种情况B胜。从而A、B二人的获胜率(机会)之比应为11∶5。因此,A应得赌金为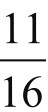 ×64=44个金币;B得其余的20个金币。
×64=44个金币;B得其余的20个金币。
(三)帕斯卡的数字三角形法(https://www.daowen.com)
帕斯卡则从他发现的数字三角(帕斯卡三角)出发。他设想:赌局开始,在数字三角的顶点上放一颗棋子,第一局若A胜,将棋子向左下移到第二行;若B胜则向右下移动棋子到第二行。第一局后,不论谁胜,棋子都会移到第二行。第二局后,棋子一定会移到第三行上。只是若A胜棋子向左下移一行,B胜向右下移一行。依此类推,第三局,棋子移到第四行。第四局后,棋子移到第五行。

图5-8-2 帕斯卡
若A胜3局,B胜1局,则棋子向左下移3次,向右下移1次。棋子移动的路线有以下四条:
1(向左)→1(向左)→1(向左)→1(向右)→4;
1(向左)→1(向左)→1(向右)→3(向左)→4;
1(向左)→1(向右)→2(向左)→3(向左)→4;
1(向右)→1(向左)→2(向左)→3(向左)→4。
则不论如何,最后棋子都移到第五行的第二个数字4上。这个数字4,恰好就是A胜3局,B胜1局的所有可能情况。
同理,第五行上第三个数字6,就是从顶点1移动棋子四次到达这个数字上的所有可能路径的总数。
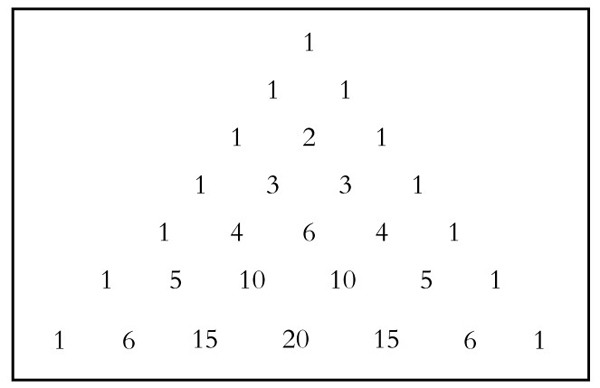
图5-8-3
因为A若胜4局、3局、2局,连同已经获胜的2局,A都先胜4局,故A胜;若A只胜1局,或全输,B才能够获胜。
因此,对应第五行上的前3个数字1、4、6就是A获胜的所有可能情况;而第五行后两个数字4、1则是B获胜的所有可能情况。于是A、B获胜的可能机会之比应为:(1+4+6)∶(1+4)=11∶5。这与上面费马的推理计算结果完全相同。
到此,梅累的得分问题,便彻底解决。
若用排列、组合符号表示,那么帕斯卡的方法和结果可以表示为:
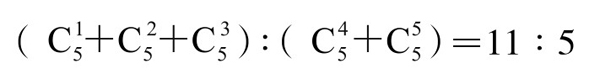
比较两人的思路和解法,虽然后者思路要复杂一些,但是利用排列组合,可以将以上问题的解法,推广到一般情况。例如,A、B二人各需再胜m局和n局,那么,终局的棋子应该落在第m+n+1行上,且二人获胜机会之比为:
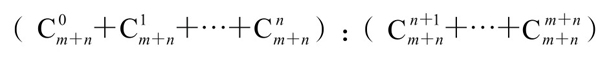
由此得分问题,引发数学家对概率论的研究,而使得随机事件的研究成为数学的重要门类。因为,在概率论问世之前,数学的研究对象虽然已经从定量发展到变量,但是对于变量之间的关系,仍然是固定的。例如行车的距离、时间和速度之间的关系一般是:距离等于速度与时间的乘积,计算公式为s=vt。然而实际上,车行进在路上,并非匀速,速度v本身是个随机变化的量。所以根据这个公式计算得到的结果,与实际结果有差距。所以,随机数学,更加接近实际情况。而由赌徒得分问题所引发的概率论,是随机数学这门大学问的源头。
