一题多解,奇思妙想
十二、一题多解,奇思妙想
数学解题不在于数量多,而在于选择好题,在解题的思路、方法上多下功夫。抓住一个问题,从多角度、多视角、多思路上去发掘解答的途径和方法。做到一题多解,一题多想,一题多用。
通常学生拿到一个题目,想出一种方法做出来了,就完事了。不去追求解答的繁简,不去考虑解法的优劣。其实,首先想到的解法未必就是最好的方法。好的解法往往在反复思考之后才能够得到。所以我们要求学生在得到题目的解答之后,应该要好好地想一想:还有更好的方法吗?努力使解法更简单,更优美。
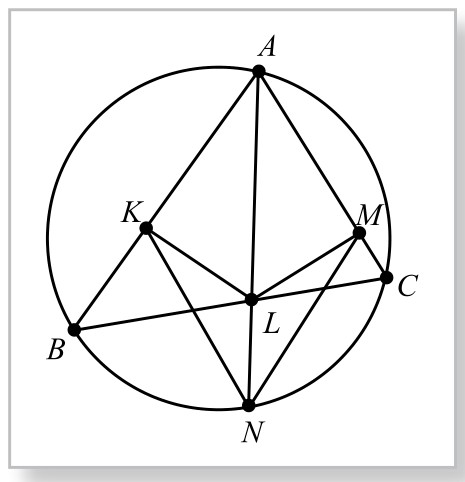
图5-12-1
例1.(I M O-28)如图5-12-1,锐角△ABC中,A角平分线AL交外接圆于N点,过L作LK⊥AB, LM⊥AC,垂足分别为K、M,求证:四边形AKNM面积等于△ABC面积。
分析和证明:这是一道不算太难的几何证明题。
证明的思路很多——割补法、面积公式计算、等积变换法等。
证法1.(割补法1)如图5-12-2,比较四边形AKNM与△ABC,有共同部分——四边形AKLM。对其余不重合的部分进行等积变形:过N点分别作NS∥LK, NT∥LM,分别交AB、AC于S、T。则△NKL与△SKL等积;△NLM与△TLM等积。
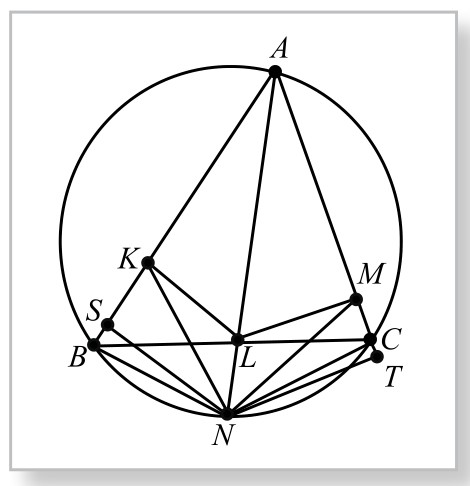
图5-12-2
如果剩下的部分——△BSL(多出的)与△CTL(不足的)等积的话,问题就解决了。即问题变成证明:S△BSL=S△CTL。
因为L在∠A平分线上,它到AB、AC的距离相等,故只需要证明两三角形的底边相等,即只要证明BS=CT即可。而这可以通过证明△BSN≌△CTN得证。
因为这是两个直角三角形,有NB=NC, NS=NT。故问题得证。
这个证明方法,是否最好呢?有没有更为简单明确的方法呢?——有。
证法2.(割补法2)如图5-12-3,四边形AKNM与△ABC公共部分为△AKM,对其余部分进行变换和割补:过N作MK的平行线,交圆于另一点A1,连接A1K、A1M,则△NKM与△A1KM等积。再连接A1L、A1B、A1C,则因四边形AKNM是菱形,知对角线AN⊥MK,而NA1∥MK,故亦有AN⊥NA1,故知AA1是圆的直径。因此∠ABA1与∠ANA1都是直角,即A1B与LK垂直于AB;A1C、LM都是AC垂线。
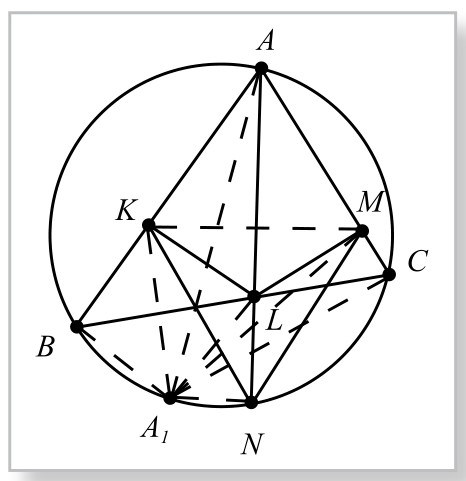
图5-12-3
从而△A1KL与△BKL等积,△A1LM与△CLM等积。又由于△LKM是公共部分,于是,凹四边形A1KLM分两部分,分别移到△ABC中。最后达到割补的目的。结论得到证明。
上述证法,都是进行两次割补,才能证明二者等积。能够一次变换而达到证明的目的吗?——请看下面妙法:
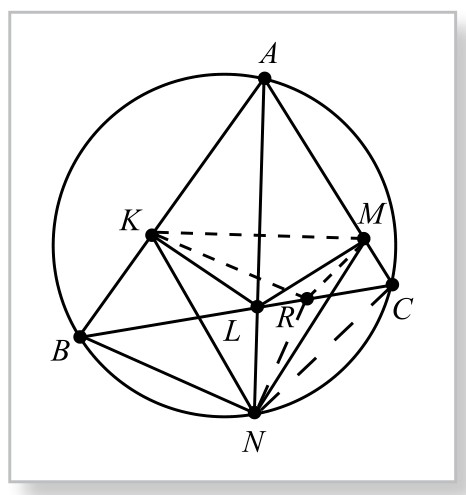
图5-12-4
证法3.(割补法3)如图5-12-4显然,因为LK⊥AB, LM⊥AC,所以四边形AKLM内接于圆,设其外接圆交BC于另一点R,连接RK、RM、RN。于是∠KRL=∠KAL=∠CAL=∠NBC,而有BN∥KR。同理可证NC∥RM。
考虑二形相同部分四边形AKRM以外的部分——凹四边形KNMR,将其分为△NKR与△NMR,分别平行移动它们顶点至B、C,则知它们分别与△BKL、△CMR等积。从而只此一次等积变换,就使四边形AKNM与△ABC等积。简便得多。
以上证明方法,都是设法进行等积变换和割补,达到所证目的。那么可以直接计算各自面积,证明二者相等吗?——可以。请看下面的证法:
证法4.(面积公式计算)连接菱形对角线KM,设△ABC的外接圆的半径为R,由正弦定理知
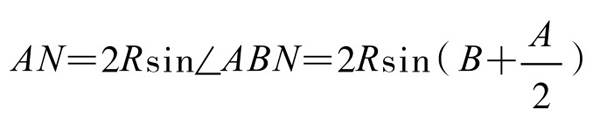
KM=ALsin A(AKLM共圆,AL为直径)
在△ACL中由正弦定理,有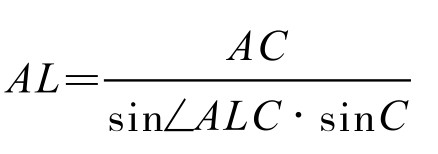
代入得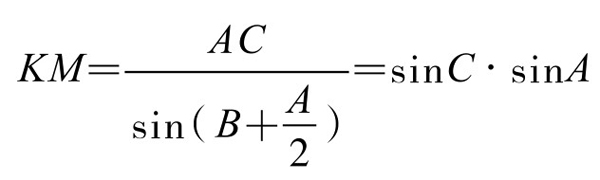
现计算菱形AKNM面积:
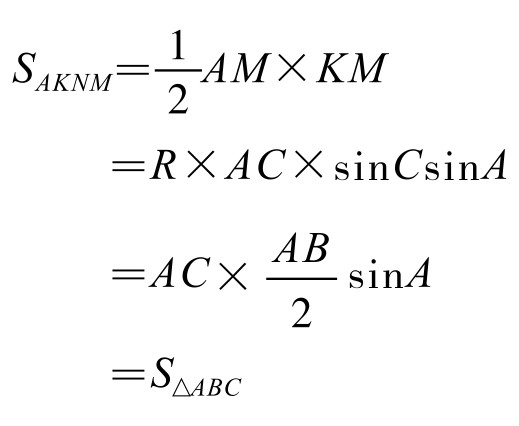
这是我国选手,一位女同学给出的新证法。多么简单,多么漂亮!
以上四种证明方法,以证法3、4两种为好。第三种想得巧妙,第四种做得轻松,最为可取。(https://www.daowen.com)
到此为止,好像已经穷尽了所有证法,特别是后两种证明方法是那样漂亮,似乎不需要再挖空心思去想什么新办法了。其实不然。还有更加精巧简单的证明方法呢!请看一位中学生的奇思妙想:
证法5.如图5-12-5,设∠A=2α,过C作CD⊥AN, D为垂足。则∠BAN=∠CAN=α。
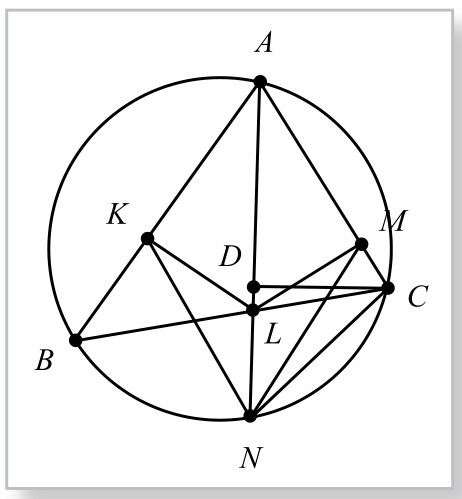
图5-12-5
于是,△ABC面积为
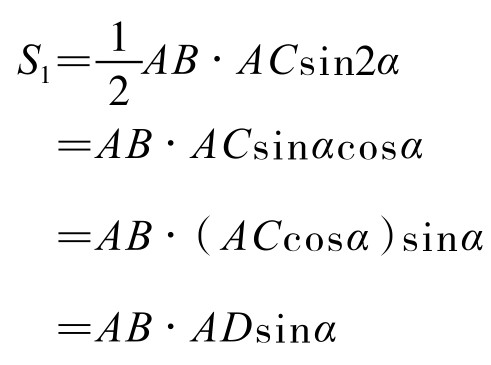
菱形AKNM面积为
S2=2S△AKN=2× 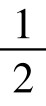 AK · ANsin α=AK · ANsin α
AK · ANsin α=AK · ANsin α
欲证S1=S2,只需证AB · AD=AK · AN或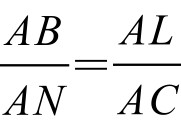 即可。
即可。
但Rt△ACD∽Rt△ALK,而有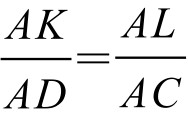 ,因此,只需证明
,因此,只需证明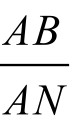 =
=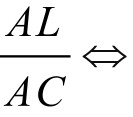 △ABN∽△ALC即可。
△ABN∽△ALC即可。
而因∠BAN=∠CAL, ∠ANB=∠ACL,故△ABN∽△ALC成立。即命题成立。
从这题的五种证明方法来看,以这一题为中心,把有关两个不同形状图形面积相等的各种证明方法都集中起来,沟通了各种方法之间的内在联系。而且将此类问题的证明思路,一一列举,加以分析和比较对数学知识的系统整理和有机联系很有好处,对数学解题方法的掌握更有好处。
例2.如图5-12-6,正方形ABCD中一点E,使∠ABE=∠BAE=15°,求证△ECD为等边三角形。
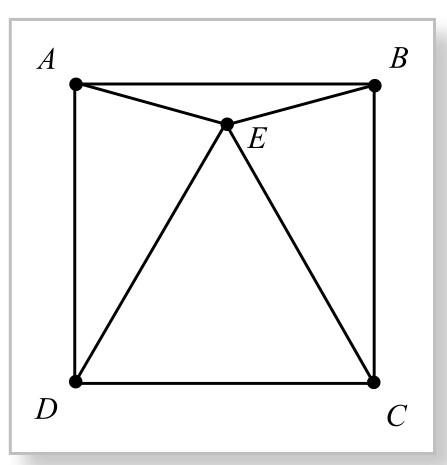
图5-12-6
题说:这是一道传统的经典几何题,以往初中数学课本,都以此题作为说明如何使用“同一法”的例题。但是,若不用同一法,则不易想到综合证法。其实直接证明的方法很多。有人曾经列举出20多种证法,其中有几种颇有巧思,值得介绍。
欲证△ECD为等边三角形,由于图形的对称性,AE=BE, ED=EC,所以,实际只需要证明ED=DC或EC=CD即可。
证法1.如图5-12-7,以BE为边向内作正△BEF,连接FC。
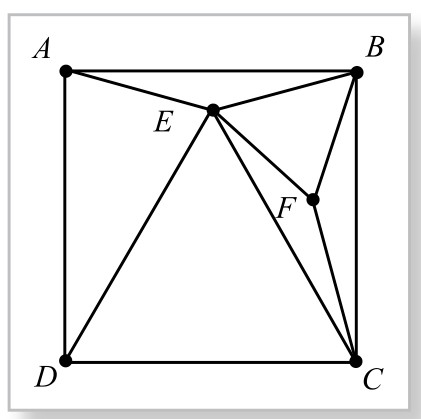
图5-12-7
在△ABE与△BCF中,BE=BF, AB=BC, ∠CBF=90°-60°-15°=15°=∠ABE,故△ABE≌△BCF。从而有∠BCF=∠BAE=15°, ∠BFC=180°-(15°+15°)=150°;∠EFC=360°-60°-150°=150°=∠BFC, CF公用。因此,△BCF≌△ECF,从而BC=EC=CD,证毕。
证法2.如图5-12-8,以AB为一边,向形外作正三角形ABF,连接EF交AB于点H。则因△ABF与△ABE皆为等腰三角形,根据三线合一性质易得EF⊥AB, EF平分∠AEB。即知∠FEA=∠FEB=75°=∠FAE=∠DAE,从而知FE∥AD,且EF=FA=AD, ADEF为平行四边形,而知AF=DE=AB=CD,证毕。
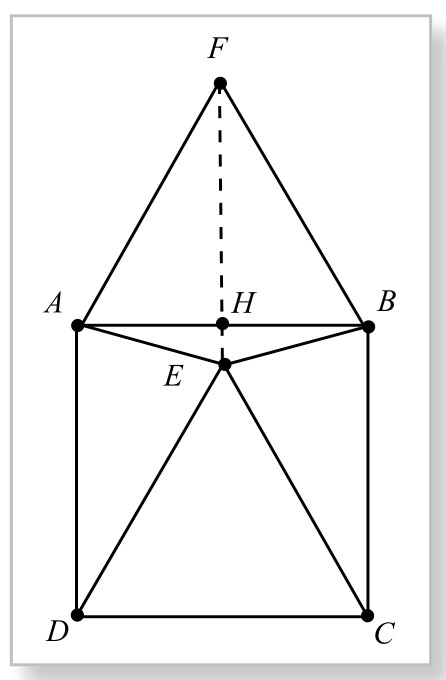
图5-12-8
以上皆是构造正三角形,下面证法则用三角计算。
证法3.如图5-12-9,设正方形边长AB=2,过E作AB、CD垂线,分别交AB、CD于F、G。由半角公式,知EF=AFtan∠FAE=AF t a n15 °=t a n15 °=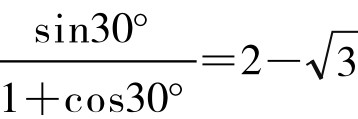 ,由此知,EG=FG-EF=2-(2-3)= 3,因而tan∠EDG=
,由此知,EG=FG-EF=2-(2-3)= 3,因而tan∠EDG=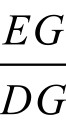 =
=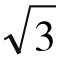 ∠EDG=60°,因此△ECD是等边三角形。
∠EDG=60°,因此△ECD是等边三角形。
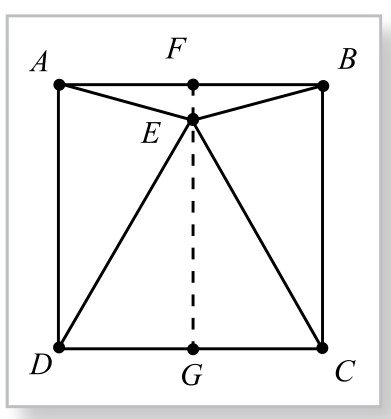
图5-12-9
下面一种证明方法,另辟蹊径,用的是“四两拨千斤”之法,更为奇妙。
证法4.如图5-12-10,设正方形一边长AB=2。过D作AE垂线DH,再过E、H作AB垂线分别交AB于F、G。则∠ADH=15°, AH=AD s i n15°, AG=AH c o s∠HAG=AH c o s15°=AD s i n15°c o s15°=AD 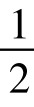 s i n30°,由此有AG=
s i n30°,由此有AG=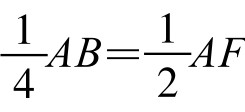 ,即G为AF中点。
,即G为AF中点。
又因EF、GH同为AB垂线,故二者平行,因而知H也是AE中点。
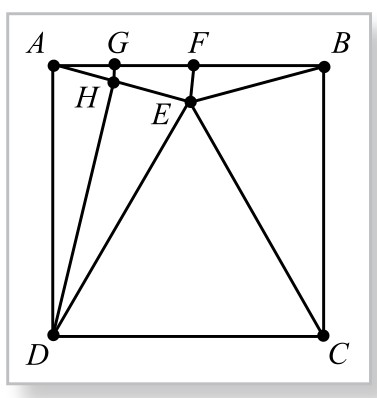
图5-12-10
于是在△DAE中,底边AE的高线DH也是底边的中线,从而△DAE为等腰三角形,即证AD=ED=DC。证毕。
奇巧吧!仅从GH计算起,发现G点是AF的中点,进而得知H是AE中点。于是证得△DAE是等腰三角形,使问题得证。这真是奇妙!
以上两种三角证法,前者用到正切的半角公式,而后者只用到正弦的倍角公式,相比之下,后者更为简单。
其他还有不少好的证明方法,留给读者去想吧。
选择内涵丰富的好题,通过一题多解的研究,可以提高我们的发散思维能力,开拓想象空间,是培养学生数学学习兴趣的重要途径。
