双马人口论数学解析
六、双马人口论数学解析
这里所说的“双马”,是指英国人口学家马尔萨斯(1766—1834)和中国人口学家马寅初(1882—1982)。
二人虽然相距百年,地理距离也相距万里,但他们都是人口学研究方面泰斗级的专家。

图4-6-1 马尔萨斯

图4-6-2 马寅初
世界上人口问题,都是重要的社会问题。但作为社会学的一个专门学问提出,始于英国的学者马尔萨斯,他在1798年发表的《人口论》堪称人口学的创始之作。他认为一个国家或地域的人口增长速度,与人口基数p(t)成正比,人口增长率为r,其数学模型为:
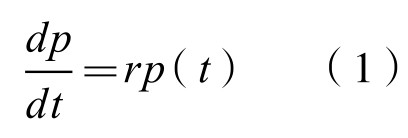
为简便起见,可以假定在短时间里人口增长率不变,即认为r是常数。于是(1)式是一阶线性齐次微分方程,容易分离变量,再积分:
由(1)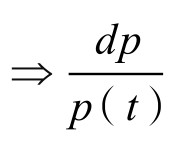 =rdt,
=rdt,
再积分得
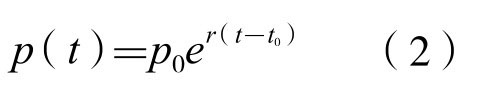
这就是所谓的人口增长的“指数模型”。
例如以1961年为起始时间t0,当时全世界人口基数为30.6亿,又假设增长率为r=0.02,即人口年净增长率为2%。那么,将这些数据代入公式(2),便得到:
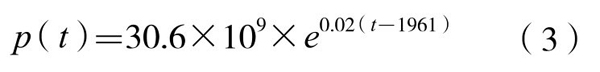
这个数学模型究竟符不符合实际情况呢?现在对上述模型进行检验:用(3)式来计算1700—1961年间,全世界人口增长情况,结果是这200年间,每34.6年人口增长1倍。而实际情况是每35年增长1倍,与理论结果非常接近。所以,马尔萨斯人口理论,曾经盛行一时。(https://www.daowen.com)
但是,若用该公式来预测未来人口增长趋势,则令人不安。因为(3)式表明:人口数量是时间的指数函数,当t→∞时,人口总数p(t)→∞。例如,用此公式计算2035年的人口,竟达到2200万亿!那时,地球上每个人立足的地方,只有1平方英尺,连站立都困难。这显然不是人们所希望的,因为地球的承载能力是有限的。
所以后来学者对马尔萨斯模型提出了改进意见,在微分方程的右边,增加一个“竞争项”,建立新的数学模型:
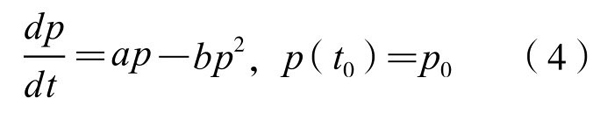
其中a, b均为常数,称为“维他系数”;第二项“-bp2”,称为竞争项。一般来说b比a要小得多。因此,当p(t)不是很大时,第二项可以省略,便成为(1)式。而当p(t)较大时,该项就必须考虑。(4)式是伯努利型的一阶微分方程,它的解为:
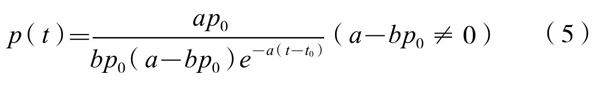
在(5)式中若令t→∞,则p(t)→ 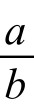 。当0<p0<
。当0<p0<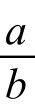 时,p(t)单调增加,函数图像大致呈S形,其拐点在p=
时,p(t)单调增加,函数图像大致呈S形,其拐点在p=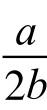 处,如图4-6-3所示。
处,如图4-6-3所示。
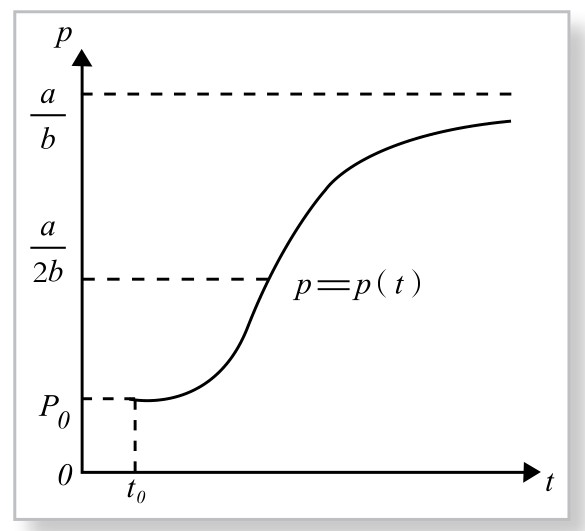
图4-6-3
由生物学实验可以推算得a=0.029,根据1961年人口实际数字,算得b=2.941×10-12。
将a、b的值代入(5)式,再令t→∞,则得p(t)→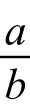 =98.6(亿),这就是所预测的未来世界人口的最大值。
=98.6(亿),这就是所预测的未来世界人口的最大值。
当然,由于世界各地社会发展情况差异很大,人口数的波动也很大,所以,公式(5)的可靠性究竟有多大,还有待于时间的检验。但是,这可以为我们制定人口政策,提供一个重要参考。
我国的马寅初先生于1957年发表了一篇重要论文——《新人口论》,提出关于我国人口控制的一种新的理论。他与马尔萨斯的不同之处是,他认为国家人口不能简单地说越多越好,而应当有所控制和计划。他的新人口论的观点是:一个国家或地区的人口增速,不仅与人口基数有关,而且应受地域资源最大承受能力的制约。每个国家和地区,都有最大可承载人口量。超过这个最大承载量,就可能造成经济和社会问题,给人们带来饥饿、疾病等灾难。中国即使地域辽阔,资源丰富,也有一个人口最大承载量(设为M)。假设现有人口为p,那么M-p就是人口增长空间。增长空间越大,增长速度就越大;增长空间越小,增长速度就应该越小。即人口增长速度不仅与人口基数成正比,与人口增长空间也成正比。于是他提出人口增长的新公式:
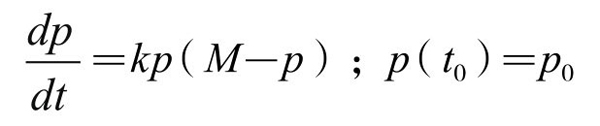
把上式改写为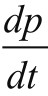 =αp-βp2。
=αp-βp2。
其中α=kM, β=k;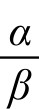 就是人口最大承载量M 。
就是人口最大承载量M 。
由此可得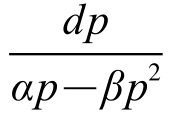 =dt或
=dt或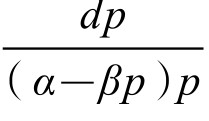 =dt。
=dt。
两边积分,得:
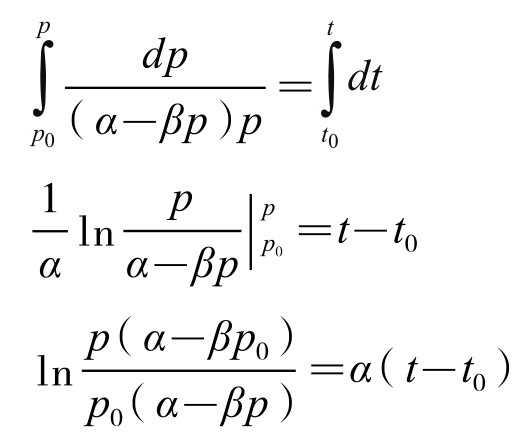
最后得到人口增长公式:P(t)=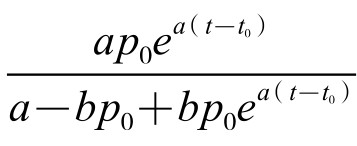 。
。
其图像与图4-6-3大致相同。
法国和美国都曾经用此公式预测过人口趋势,计算结果与实际情况吻合。我国以此公式为依据,用1990年全国人口普查数据,若按照千分之一人口增长率计算,再由生态学家测得的α=0.029,可以算得β值约为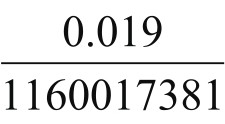 。带入上述公式,可以算得p(t)当t→∞时的极限值:
。带入上述公式,可以算得p(t)当t→∞时的极限值:
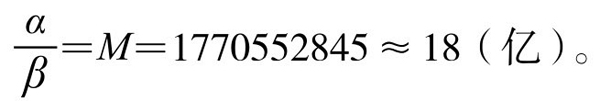
即如果按照马老当时提出的人口政策(实行计划生育),我国人口增长的极限值,可限制在18亿以内。仁者长寿,马寅初先生活到了100岁,在2019年中华人民共和国成立70周年之际,他被评为“最美奋斗者”。
