五、数与算式之美
五、数与算式之美
(一)数字之美
数字,即1, 2, 3, …,何美之有?且看下面的举例。
1.奇数与偶数
1, 3, 5, …奇数者也,有无穷多个。2, 4, 6, …偶数者也,也有无穷多个。它们二者相间排列,构成整个正整数集合。
两个奇数之和为偶数,而两个偶数之和,仍为偶数。一个奇数与一个偶数之和却是奇数。
关于偶数有一个著名的猜想——哥德巴赫猜想:任意一个大于5的偶数,可以表示为两个素数之和(简称为N=“1+1”问题)。欧拉将其改为等价命题,任意偶数n,只要n>5,就可表示为两个素数之和,如8=3+5,10=5+5,12=5+7,14=7+7, …有人已经用计算机对大于5的10万以内的偶数进行验证,这个猜想都正确。但是因为偶数无穷多,不可能一一验证。用实际计算去逐个验证的不完全归纳法,是无法证明此猜想的。时至今日,这个猜想,仍旧只是猜想。
在100多年前,1919年,挪威数学家布伦,将哥德巴赫猜想弱化,改作:任何一个大于5的偶数都能够表示为两个素数因子不超过6个的合数之和,简称为N=“6+6”定理(1932年已被英国埃斯特曼证明)。由此思路前进,合数的因子个数被不断缩小。到1940年,已经有人证明了N=“4+4”。这之后,我国数学家王元连续证明了N=“3+4”和N=“2+3”。
与此同时,匈牙利数学家兰恩开辟了另一条思路——大偶数是一个素数与一个不超过6个素数因子的合数之和,他证明了N=“1+6”。我国数学家潘承洞于1962年证明了N=“1+5”,紧接着,王元证明了N=“1+4”。1966年“文革”前夕,陈景润证明了N=“1+2”。这是迄今为止世界上最好的结果,被称为“陈式定理”。
你看,从一个不起眼的偶数问题,引出了如此激动人心的大问题。这真是数学花圃中的一朵奇葩。
哥德巴赫猜想,也可以用奇数来表述:任意一个大于7的奇数,可以表示为一个奇数和两个素数之和。其实质与上述猜想内容一致。因为任何一个大于7的奇数,总可以分成奇数3与一个大于5的偶数之和,这便成为前面欧拉改述的猜想的表述。
2.素数与合数
所谓素数,就是除了1与它本身以外,没有其他因数的正整数。最小的素数是2,接着便是3, 5, 7,11,13,17,19, 23, 29, 31, 37, 41, 43, 47, 53, 59, …除了第一个素数2是偶数外,其他所有素数都是奇数。
关于素数的第一个话题,就是素数有多少个。前面已经说过,素数有无穷多个,而且首先是由欧几里得在《几何原本》中用反证法证明的。
从素数序列的前几个素数,便可以发现,素数的分布是不规则的。在1—10区间内有三个素数,在11—20区间内却有4个素数,在21—30区间、31—40区间内各有2个素数,在41—50区间内有3个素数。那么,素数的分布到底有没有规律呢?这是个至今还没有定论的数学难题。正因为是个极难的难题,所以,一直吸引着很多数学家关注和努力攻关,虽然尚未解决,但是已经发现很多有趣的、关于素数分布的逼近公式。
3.孪生素数
在素数序列中有一些相邻的素数(两数间只隔一个偶数),如3, 5, 7(一组“三胞胎”),11与13,17与19, 29与31, 41与43等,都是孪生素数,100以内有8对孪生素数,最大的一对是71与73;1000以内有35对孪生素数,最大的一对是881与883。但与素数出现的情况一样,孪生素数也有无穷多个,其分布也无规律可言。例如在601—700之间有3对孪生素数(617与619, 641与643, 659与661),但在661—809之间,间隔超过140个数字,却没有一对孪生素数!
到2002年,人们找到的最大一对孪生素数为33218925× 2169690-1与33218925×2169690+1,是18072位的大数。但是,关于孪生素数是否有最大值,或者说,孪生素数是否有无穷多个,到目前为止,也没有定论,是个未解之谜。
4.完全数
一个正整数N,如果它的所有因数(除去它本身)之和,正好等于它自身,即被称为完全数。最小的两个完全数是6和28。试看,6的因数为1, 2, 3,而1+2+3=6。28的因数有1, 2, 4, 7,14,它们的和为1+2+4+7+14=28。
完全数,最早是毕达哥拉斯学派提出来的。他们认为这样的数非常完美,故以“完全数”命名之。欧几里得在《几何原本》中还给出一个判别完全数的定理:如果1+2+22+23+……+2n-1=2n-1是素数,则2n-1(2n-1)是完全数。6和28,分别对应n=2, 3的情况。后来,人们根据这个定理,找到一系列完全数。如对应n=5,得496;对应n=7,得8128,都是完全数。
1644年法国数学家梅森提出猜想:当n=2, 3, 5, 7,13, 17,19, 31, 67,127, 257这11个素数时,2n-1是素数。后经多位数学家验证果然如梅森所言,分别找到对应的11个完全数。其中第8个对应n=31的完全数,是由已经双目失明的欧拉,仅凭心算得出的,堪称奇迹。为纪念这位猜想大师,人们把形如2n-1的数,称为“梅森数”。不过,梅森漏掉了一个n=61(素数),其对应的M61=261-1也是一个梅森数,261-(1 261-1)是第9个完全数。到2013年为止,已经发现的梅森素数有48个,最大的一个,其数字位数超过1000万。
但是,数学家科尔于1903年却证明当n=67(素数)时,对应的M67=267-1不是素数,而是一个合数。从而对梅森猜想给出了否定证明。
这个故事说明,数学的某些猜想,在没有彻底证明之前,只能是猜想。而如果能举出一个反例,便立即给予否定证明。2010年,年仅21岁的中国年轻数学家刘路,就是用举出反例,证明(否定证明)了“西塔潘猜想”(后面还要细说)。
如果把一个正整数的所有因数(包括该数本身)相加,和等于该数的2倍,则说这个数是2倍完全数。那么,有没有3倍,以至多倍完全数呢?回答是肯定的。
据王青建编著的《数学开心辞典》(书末所附参考文献[8])所载,现在发现的3倍完全数有6个,其中最小的是120。120的因数有1, 2, 3, 4, 5, 6,8,10,12,15, 20, 24, 30, 40, 60,120,容易求得它们的总和等于360,恰是本数120的3倍。
经数学家和数学爱好者们不断努力,人们还发现30240和32760是两个4倍完全数,以及5倍,乃至8倍完全数。目前已经发现的多倍完全数超过1000个,其中8倍完全数就有400多个。可见,仅就正整数而言,关于完全数这一个特种数,就是个“富矿”,有那么多丰厚的宝贝可挖。
5.亲和数
与完全数有关系的,是亲和数。其意义是:若A, B是两个正整数,而A的所有因数(不包括该数本身)之和等于B;B的所有因数(不包括该数本身)之和等于A。那么,就称A, B为一对亲和数。第一对亲和数是220和284,是毕达哥拉斯发现的。读者可以自行验证。自那以后,寻找亲和数的进展很慢。因为寻找亲和数,关系到两个数的因数,要发现它们,就困难多了。直到1636年,法国“业余数学之王”费马才发现第二对亲和数,17296=24×23×47与18416=24×1151(读者可以自行验证)。其后笛卡尔也找出一对亲和数(据书末参考文献[10])。到1750年,大数学家欧拉一口气找出59对亲和数(他发表的62对亲和数中有3对错误)。欧拉的杰出数学发现,鼓舞了很多后来者,不断发现新的亲和数。至今人们已经发现1000万多对亲和数。其中有一对较小的亲和数(1184和1210)是由一个16岁的小男孩发现的。
亲和数的推广形式,是多个正整数因数之和循环一圈:A的因数和等于B, B的因数和等于C, ……最后又回到原来的A。例如12496(A)的真因数(不包括该数本身)之和为14288(B), B的所有真因数之和等于15472(C), C的真因数之和等于14536(D),而D的真因数之和等于12496,又回到了原来的正整数A。于是A→B→C→D→A形成5个循环亲和数。
6.雷劈数(卡普利加数)
印度数学家卡普利加(Kaprekar)在一次雷阵雨后,见到公路旁一块标有数字3025的里程碑被雷劈为两段,其两块上的数字分别为30和25。作为数学家,卡普利加对数字有特殊的敏感性。他敏锐地发现这两个数字之间有着巧妙的联系:两块上的数字相加之后再平方,竟又回到原来的数,即
(30+25)2=552=3025
于是,人们便称这类数为卡普利加数,或雷劈数。
这种奇怪的“雷劈数”,还有别的吗?至今人们已经找到几十个这样的“雷劈数”。例如:01, 09, 45, 99, 703, 22222, …
452=2025,而20+25=45;
992=9801,而98+01=99;
7032=494209,而494+209=703;
222222=493817284,而4938+17284=22222;
…………
近来,有位数学老教授李长明先生发现一类有趣的卡普利加数。文章发表在《高等数学研究》上。
7.数字排列和移动
a)将1, 2, 3, …, 9这九个数字排列成三行,使其成三个三位数a, b, c,能否使b=2a, c=3a?这是一个实习教师,面对一群顽皮的初二“差班”学生临时想出来的一道智力游戏题。谁知,就是这道数字排列题,把躁动的学生“镇住”了,使得他们逐渐安静下来,认真思考。而且有一位学生居然还想出了一个正确答案。这说明有趣的数学题,能够引起学生的兴趣,促进其对数学题目的积极的思维活动。
那么,这个数字问题的答案是什么呢?那个学生首先得到的答案如下:
a=327, b=654, c=981。
其实,除此以外,还有三组答案:
a=273, b=546, c=819;
a=192, b=384, c=576;
a=219, b=438, c=657。
至于是否还有别的答案,倒是个困难的问题。因为,一时找不到,并不等于不存在其他答案。这需要仔细分析,排除一切其他可能。
b)在等式中能够移动的数字
一般来说,在一个确定的数字等式中,各个数字的位置是固定的,不能随便移动。不然,等式便要被破坏。但是有的等式中的数字,却很奇怪地可以移动,而使等式仍然成立。当然这种情况是罕见的。正是因为罕见,所以人被好奇心驱使,容易产生研究兴趣。《数学开心辞典》中提供了一些有趣的实例。
例1.在由1, 2, …, 9组成的等式18×297=5346(数字不重复)中,能够将其中的数字9,从297中移动到1,8之间,而使得等式仍然成立,即198×27=5346。
你感到惊奇吗?这就是数学的奇异美!你还能发现其他类似的能够移动数字的等式吗?——请看:
例2.27×594=16038,将9移动到2与7之间,而得297×54=16038;36×495=17820,将9移动到3与6之间,而有396×45=17820。
这两个等式中的9,都从乘式的第二个数中移动到第一个数的两个数字之间。多么奇怪,又多么美妙啊!至于其他类型的等式中也有类似怪异的现象出现。
例3.以下无理等式,数字可以自由进出根号:
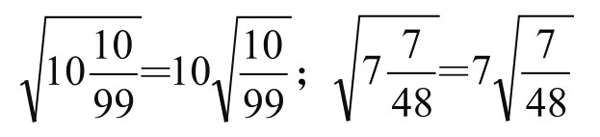
一般的有: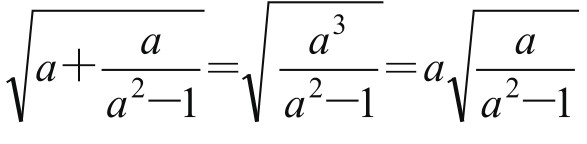
可见,数字移动到根号外,是有理论根据的,并非随便移动。
数字能够移动,运算符号也能在等式中移动。例如:
例4.8×767123287=876712328×7
奇怪吧!算式中数字的顺序没有变,而其中的乘法符号“×”,却从开头移动到了末尾。
后来人们还发现数字等式中指数符号也能够下移。请看:
例5.25×92=2592;34×425=34425。
例6.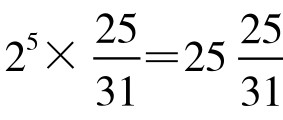 ;
;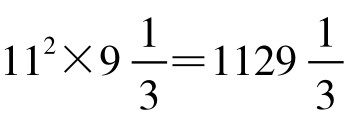 。
。
数字等式中这种数字、运算符号移动的奇异现象,还有许多。读者可以在书后的参考文献中找资料去看,或者自行研究。或许能够发现数字等式中一些新的意想不到的奇异之美。
(二)异形算式的奇异美
1.循环节的循环
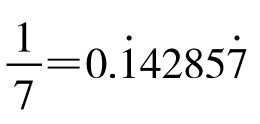
这是以7为分母的单位分数,是个循环小数,循环节为6位。若将这个循环节6位小数分别加倍,便得到其各个倍数如下:
2×142857=285714;
3×142857=428571;
4×142857=571428;
5×142857=714285;
6×142857=857142。
若再以7相乘,则得全9数:7×142857=999999。
其实,如此情况是有数学理论根据的。凡是素数p,以p为分母的单位分数,有p-1位数字循环节,则必有以此循环节倍数循环的现象;若以p相乘,则必得全9数。例如以19为分母的单位分数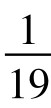 ,是个有18位小数循环节的循环小数。其循环节的倍数,也有类似现象。
,是个有18位小数循环节的循环小数。其循环节的倍数,也有类似现象。
2.“吉祥数”8
8,这个普通的数字,在某些地方(如我国南方)被美化,甚至是被神圣化。例如,宾馆或酒楼,即使是二、三层楼的房间(包间),也要编号为281, 282, …或821,822等等。
在数字算式中,含8的数字,也有特别的花样形式。
例1.正整数的平方数的末尾数,只能是0,1, 4, 5, 6, 9,不可能是8。但是正整数的立方数的尾数,却可以是8,88,888。
立方数的末尾数为8的正整数尾数只能为2。经检验,一位数只有2一个;两位数有两个:42和92,它们的立方数的尾数均为88:423=74088, 923=778688。
立方数尾数为888的正整数只能是三位数,共有四个:192, 442, 692和942。
例2.数字8的魔力分数数列:
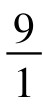 ,
,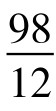 ,
,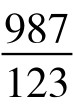 ,
,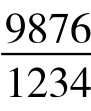 ,
,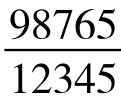 , …,
, …,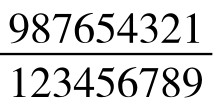
分子递减,分母递增。这个分数数列,还可以延续。分子依照递减法则,应该为:9876543210, 98765432100+(-1)=98765432099,987654320988, 9876543209877, …分母则递增,应该加10,但又只增加一位,故为1234567900,以下应该是12345679011,123456790122,…若寻其规律,分母可表示成无穷级数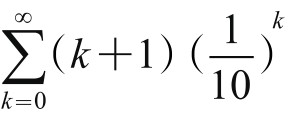 ,分子则为
,分子则为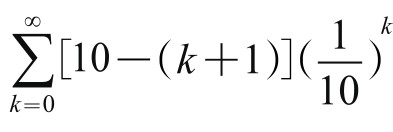 。
。
分子数列之和为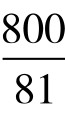 ,分母数列和为
,分母数列和为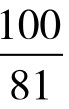 。
。
二者相除则得商数,恰好是8。亦即上述分数无穷数列中,分子数列之和,与分母数列之和,二者之比,恰好是8。岂不妙哉!
3.缺8数的奇妙性质
N=12345679是个缺8数,我们来看它的9倍数有何特点:
9N=111111111, 2×9N=18N=222222222,
3×9N=27N=333333333, …, 9×9N=81N=999999999。
若用3的倍数(9除外)去乘它,则又会得到另一类特殊形式的“三位一体”数,如:
3×4×N=12N=148 148 148, 3×5×N=15N=185 185 185,
21N=259 259 259, 24N=296 296 296, 78N=962 962 962……
如果倍数再大一些,乘积便增加一位,但也有奇异的形式。如:
84N=1 037 037 036,87N=1 074 074 073,
165N=2 037 037 035,807N=9 962 962 953……
把首位数加到末尾数上,仍然是“三位一体”。
4.宝塔算式
132=169
1332=17689
13332=1776889
133332=177768889
可以再往下算出宝塔的基层。
又如:22×22=484
222×22=4884
2222×22=48884
22222×22=488884
…………
多么有趣的算式宝塔!类似的算式宝塔,还有很多。有兴趣的读者,可以参看王青建先生主编的《数学开心辞典》。
5.无据算式
例1

例2

这两个算式,若按算术运算法则来说,是没有根据的,即是无据运算。但是其最后结果,确实正确无误。容易算得:
8888×3333=29623704;77777×66666=5185081482。
