追求π精确史上的数学巧思
四、追求π精确史上的数学巧思
(一)人类对于圆周率π精确近似值的不断追求
在前面,我们已经对圆周率π近似值的研究历程,做过叙述。大致分为三个时期:几何方法(割圆术)时期、分析时期以及机器计算时期。目前用计算机求得π的近似值已经超过10万亿位,远远超过实际运用的需要。但是,无论是在初期人们手工计算,还是运用分析公式计算,都经历了十分艰难的过程。例如最后一位手工计算纪录创造者——数学家鲁道夫(1540—1610),用割圆术几何方法,计算出圆周率小数点后35位准确值,创造了用几何方法计算的最高纪录,为此,几乎用尽了他一生的精力。而人类在追求π精确近似值上花费了几千年的漫长时间。
分析时期,从法国数学家韦达(1540—1603)开始。他发现π的无穷数列或无穷分析表达式,开始用分析方法,来求得π近似值,到1947年美国人伦奇用分析方法,手工计算出π的808位小数近似值,创造人类用纯手工计算的最高纪录。就是说从π的35位小数提高到808位,用了将近300年。而自从1946年人类发明电子计算机以后,利用计算机编程,上机运算,得到的π值的小数位飞速上升。1949年第一次用电子计算机计算,就得到π的2037位小数近似值,以后更是直线上升:
1961年:100265位;
1967年:500000位;
1983年:8388608位;
1989年:超过10亿位;
1995年:达到64亿位……
可见,数学发展之快,其中计算技术和计算方法的更新换代,显示出巨大威力。
然而在数学史上,对于π近似值的探究中,也有一些奇葩的故事。其中所蕴含的数学思想方法,特别是一些奇思妙想,有着精彩的思维之美,值得我们欣赏和借鉴。
(二)阿基米德首创割圆术
公元前3世纪,古希腊数学家阿基米德(前287—前212)首创割圆术,用圆的内接正多边形和外切正多边形,不断倍增其边数,用其周长来不断逼近圆的周长。阿基米德用圆的内接正n边形周长Cn、外切正n边形周长Pn,从内外两方面来逼近圆周。并且用几何方法,证明了关于Cn和Pn的递推公式:
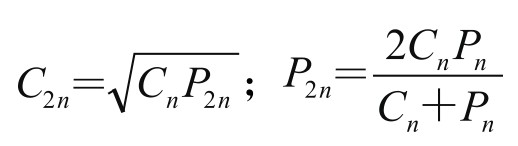
即圆内接正2n边形周长C2n是内接正n边形周长Cn与外切正2n边形周长P2n的几何平均值;而圆外切正2n边形周长P2n,是内接正n边形周长Cn与外切正n边形周长Pn的调和平均值。
若将圆外切正多边形与内接正多边形周长,从六边形开始,排列成一列:
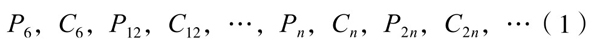
若设圆的半径R=1,那么,C6=6, P6=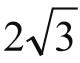 。于是,从数列的第三项起,利用这两个公式,就可以依次计算P12, C12, P24, C24等值。多么简单!
。于是,从数列的第三项起,利用这两个公式,就可以依次计算P12, C12, P24, C24等值。多么简单!
公式的证明,只需要以多边形的一边来进行考虑即可。简证如下:
如图5-4-1,设AB=an为圆O内接正n边形边长,AF=BF= 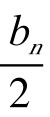 为圆O外切正n边形边长之半,AC=BC=a2n为圆O内接正2n边形边长,DE=b2n为圆O外切正2n边形边长,而C为DE的中点。则由△ADC∽△ACB, △AFB∽△DFE,从而有
为圆O外切正n边形边长之半,AC=BC=a2n为圆O内接正2n边形边长,DE=b2n为圆O外切正2n边形边长,而C为DE的中点。则由△ADC∽△ACB, △AFB∽△DFE,从而有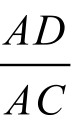 =
= 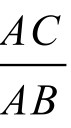 AC2=AB·AD,即
AC2=AB·AD,即
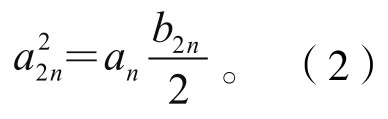
及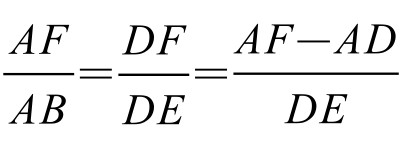 ,即
,即
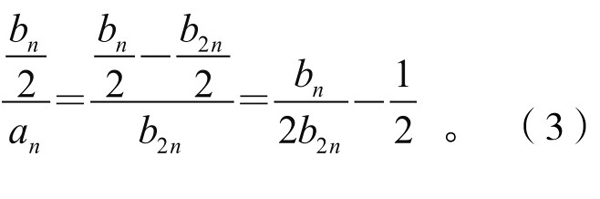
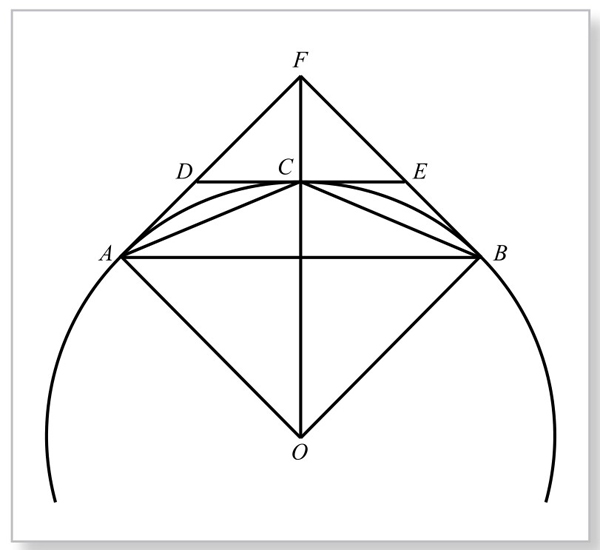
图5-4-1
将(2)式两边同乘以(2n)2,有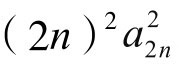 =(2n)2 ·
=(2n)2 · 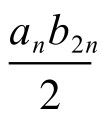 。此即
。此即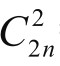 =CnP2n或C2n=
=CnP2n或C2n=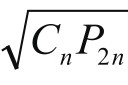 ;亦即C2n是Cn, P2n的几何平均值。
;亦即C2n是Cn, P2n的几何平均值。
将(3)式两边同乘以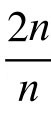 ,有
,有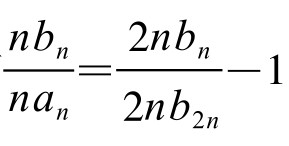 ,或
,或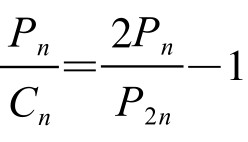 。两边除以Pn,得
。两边除以Pn,得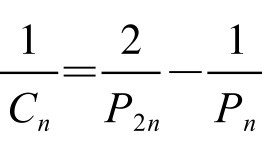 或
或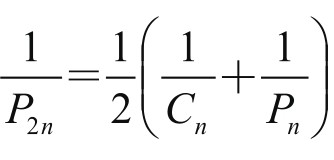 ,亦即P2n是Cn,Pn的调和平均值。
,亦即P2n是Cn,Pn的调和平均值。
他发现的这两个递推公式是很高明的。这样就能从正6边形开始,利用这两个递推公式,倍增圆内接和外切正多边形的边数,依次计算得圆内接、外切正12、24、48、96边形周长序列(1),从而得到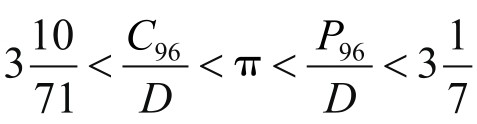 ,其中D是圆的直径。由此求得圆周率π的近似值,以及其上界和下界。如果取π精确到0.01的近似值,那就是π≈3.14。
,其中D是圆的直径。由此求得圆周率π的近似值,以及其上界和下界。如果取π精确到0.01的近似值,那就是π≈3.14。
(三)刘徽对割圆术的改进
刘徽是中国魏晋时期(公元3世纪)的数学家。他呕心沥血为《九章算术》作注,为中国古代数学作出了许多杰出贡献,其中就包括他所独立创造的“割圆术”和“徽率”。
《九章算术》第一章“方田”三十一、三十二题是圆的面积计算题,用的公式为“半周×半径=圆面积”;在具体计算时,以π=3入算,即圆面积=3×半径×半径。(1)
结果误差较大。对此,刘徽作了长篇注文,以求改进。
他首先指出,以π=3按公式(1)算出的结果,不是圆的面积,而是圆内接12边形的面积。为什么呢?请看图5-4-2:设圆半径为r, ABCDEF为圆的内接6边形,其一边之长AB=r。
现将圆内接正6边形“割”成正12边形。其中四边形OAPB是筝形,它的两条对角线AB和OP互相垂直且都等于半径r,它的面积等于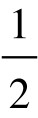 ×AB×OP=
×AB×OP=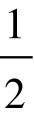 ×r×r。
×r×r。
而圆内接12边形恰好由6个这样的筝形组成,所以,它的面积是S12=3r2。因此,用公式(1)来计算圆的面积,显然是不妥当的。若以π=3作圆周率来计算圆面积,会造成较大误差。
其次,他进一步将圆内接正12边形“割”成正24边形、正48边形、正96边形,并用这些圆内接正多边形的面积来近似表达圆的面积。
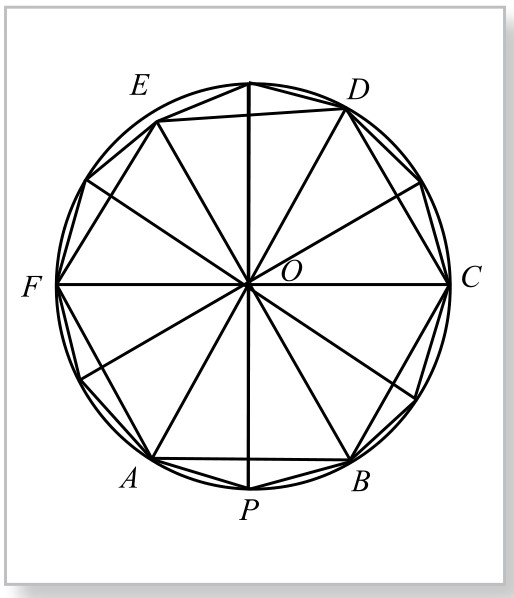
图5-4-2
为了求出这些多边形的面积,他设圆的半径为1尺,用勾股定理算出它们一边之长a12, a24, a48, a96。仿照上面的办法,用筝形面积公式算出圆内接正96边形和内接正192边形的面积:
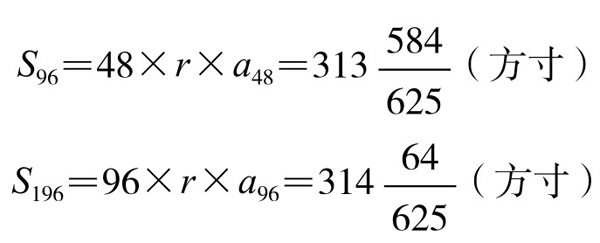
最后,推导不等式(现称“刘徽不等式”):
S192<S圆<S192+(S192-S96)
在图5-4-3中,设AB为圆内接正96边形的一边,AC=BC为圆内接正192边形的相邻的两边,EF为过C点的切线,ABFE为矩形,OC=OA=OB为半径。显而易见,扇形O-ACB的面积S扇界于筝形OACB面积S筝与五边形OAEFB的面积SOAEFB之间:
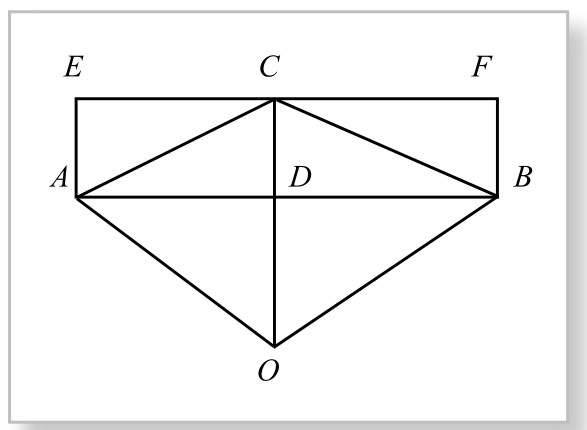
图5-4-3
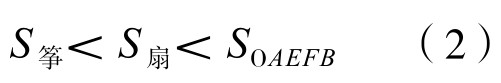
而SOAEFB-S筝=S△ACE+S△BCF=S△ACD+S△BCD
=S△ABC=S筝-S△OAB
故(https://www.daowen.com)
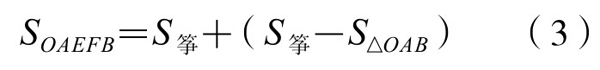
将(3)式代入(2)式右边,得
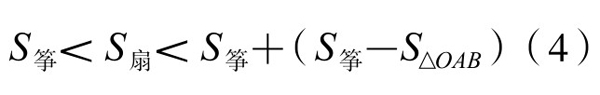
将(4)式两边同乘96,得
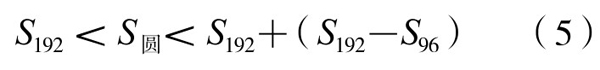
一般地,对于正整数n而言,我们有刘徽不等式S2n<S圆<S2n+(S2n-Sn)。将S96、S192的数值代入(5)式,得

“弃其余分”之后,求得近似值S圆≈314(方寸)。因为圆的半径为1尺,所以间接地求得圆周率π≈3.14。
前面说,刘徽独立地创用割圆术,但在世界科学史上,“割圆术”不是刘徽的首创,而是古希腊数学家阿基米德的首创。这并不妨碍尊重刘徽的独立创造之功,而且不等式(2),确是刘徽的个人创造,现在我们仍然把它叫做“刘徽不等式”。利用这一不等式,只需要计算圆的内接正多边形面积,不用再计算圆的外切正多边形面积,就可以同时得到圆周率的上界和下界。这也是刘徽工作的优点。
(四)从3.14到3.1416
阿基米德和刘徽,都是用割圆术算得π≈3.14,只有两位小数近似值。
这在精密计算中,略显粗糙。如何能在割圆术的基础上,进一步提高π值的近似小数数位呢?中国古代数学家祖冲之(429—500)做出了重大贡献。他先将3.14提高到3.1416,以后又进一步创用新法,得到π的七位小数近似值,并将这一纪录保持一千年以上。这节先讲他是如何得到π的四位小数近似值3.1416的。
π的两位小数近似值3.14,在我国常被称为“徽率”。而四位小数近似值3.1416,因为远比3.14精确,因此也被称为“优率”。
“优率”出自《九章算术》注中,但这段文字是刘徽所注,还是祖冲之所注,至今未有定论。若为刘徽所注,则在公元263年之前;若为祖冲之所注,则在公元462年以前。不论何者(依据作者考证,这段文字系祖冲之所注),在世界上都是最早的。国外,它最早出现在印度数学家阿耶波多(476—550)的《阿耶波多历算书》(499年)中,比中国的文献要晚。
从3.14到3.1416,不仅是精确度有很大的提高,而且在推导的方法上也有本质上的改进。从《九章算术》关于推导“优率”的注文来看,优率的导出,用了“外推归纳法”。方法如下:
刘徽在求得徽率的计算时,设圆的半径R=1(尺),圆内接正6、12、24、48、96、192边形的面积已经求得,分别为
S6=2.598076, S12=3,
S24=3.1058286, S48=3.1326286,
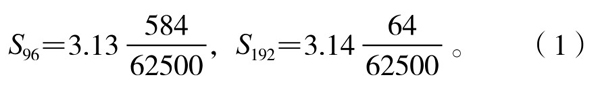
为了估计Sn随着n增大的变化趋势,作上述数列前后两项之差,得到以下“差幂”序列:
△6=S12-S6=0.401924, △12=S24-S12=0.1058286,
△24=S48-S24=0.0268, △48=S96-S48=0.006716,
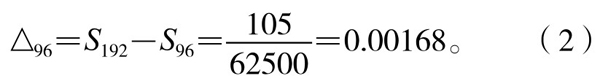
作此序列后项与前项之比,得差幂的增长率序列:
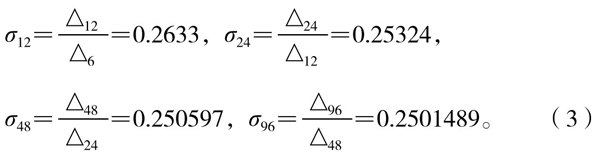
与前两个序列相比较,序列(3)有按比例变化的趋势(可以称为“拟等比数列”)。如果以正12边形S12为准(即“以十二觚之幂为率消息”),它与前后项“差幂”之比σ12≈0.26作为此“拟等比数列”公比的话,那么就能“外推”得:
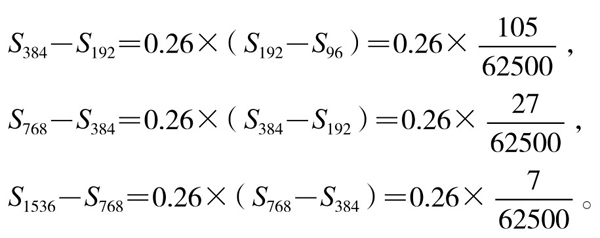
三式相加,得S1536-S192=0.26× 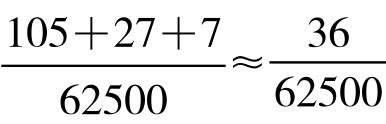 。
。
于是得到
S圆≈S1536=S192+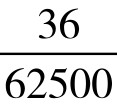 =
=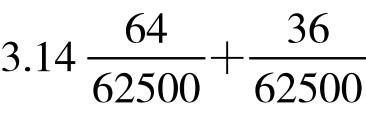 =3.1416(尺2)。
=3.1416(尺2)。
考虑到圆的半径为1(尺),所以得到的圆面积值,就是圆周率近似值π≈3.1416。这便是“优率”的由来。
从以上推导过程来看,仅根据刘徽已有的数据,无须继续割圆,就得到如此高精确度的“优率”,实在巧妙得很!在方法论上,是一个了不起的创造。
(五)祖冲之发现“盈朒”二数的巧思
我国古代伟大的数学家祖冲之(429—500),以其关于圆周率研究的杰出成就享誉世界。他求得“盈、朒”二数:
3.1415926<π<3.1415927
领先世界超过千年。可惜由于祖冲之的著作《缀术》早已失传,他究竟是怎样推出这“盈、朒”二数和“祖率”的,却成了千古之谜。作者曾经根据《隋书·律历志》等史料,比较了刘徽和祖冲之关于圆周率研究的异同,提出了对祖冲之关于“盈、朒”二数算法的合情推理,以探求祖冲之伟大创造的思路和方法。其思想方法大致如下:
1.刘徽设圆的半径为1单位(尺),从计算圆的内接正多边形面积出发,通过求圆面积,间接地求得圆周率近似值——徽率π≈3.14。祖冲之则设圆的直径为1(丈),计算圆内接正多边形的周长,直接得到圆周长的近似值,从而求得圆周率近似值。为了使计算简化,他导出了圆内接正多边形周长的递推公式:
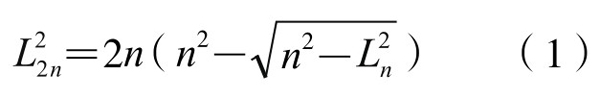
证明如下:如图5-4-4,设圆直径AP=d=1(丈), AB=an, AC=a2n, CE=cn,于是
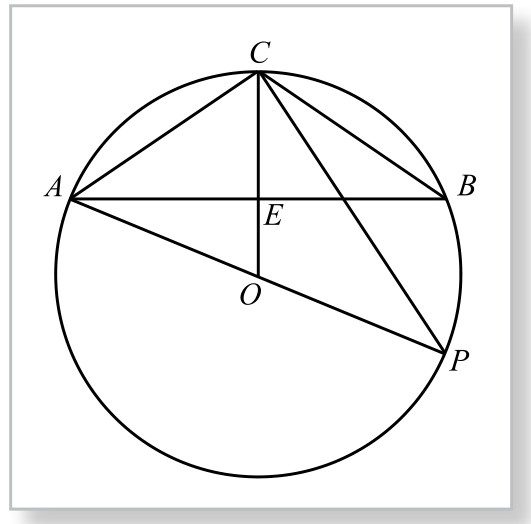
图5-4-4
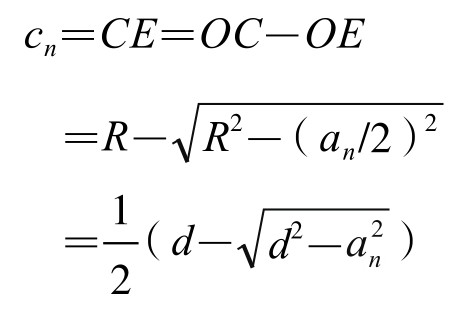
由Rt△CAE∽Rt△APC,得CE∶AC=AC∶PA,即cn∶a2n=a2n∶d,从而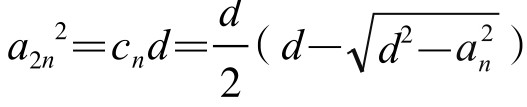 。
。
将d=1(丈)代入,再乘2n2,便得公式(1)。
2.计算圆内接正多边形周长序列{Ln}前几项,求其差序列和比序列,并以此来探究Ln的增长趋势。
从L6=3开始,利用公式(1),依次算出L12、L24等。每次开方取8位小数,并对第8位小数“四舍五入”,得

其中圆括号()内的第8位小数已按四舍五入处理过了;以下同此。
做序列(2)前后两项的差序列:
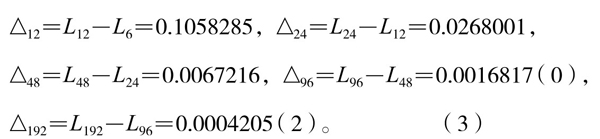
再做序列(3)后项与前项之比序列:
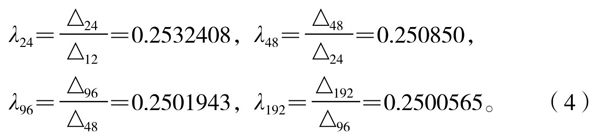
由此可见,序列(3)似乎逐渐趋向于一个定值(0.25),因此称此近似的等比数列为拟等比数列。
取λ=λ192为此拟等比数列(3)的“公比”,来估计L384, L768, …, L12288之值。
假设拟等比数列(3)从△192以后为以λ为公比的等比数列,那么便得到递推公式:
△384=L384-L192=λ△192,
即L384=L192+λ△192=3.1415576(9)。
同理可得
L768=L384+λ△384=L384+λ2△192=3.1415839(8),
L1536=L768+λ3△192=3.1415905(6),
L3072=L1536+λ4△192=3.1415921(0),
L6144=L3072+λ5△192=3.1415925(1),
L12288=L6144+λ6△192=3.1415926(1)。
若用L12288作圆周的近似值,再用刘徽不等式,就得到了盈、朒二数:
L12288=3.1415926<L圆=π<L12288+(L12288-L6144)=3.1415927。
从上述合情推理可以看出,祖冲之在计算圆周率“盈、朒”二数过程中,不囿于前人成法,表现出了高超的数学智慧和创造精神。祖冲之的这一数学成就超越时代千年之久,真是个奇迹。
