二、万类归宗
二、万类归宗
人类社会的发展,有赖于科学技术的发展和进步。而数学是打开科学的金钥匙,是各种科学技术的基础。马克思曾经在《数学手稿》中阐述数学对于社会发展和科学技术的作用,他说:“一门科学,只有当它成功地运用数学时,才能达到真正完善的地步。”事实证明,各门类科学,首先是物理、化学,然后是生物、经济学,接着是人文科学、生态学、环境科学、社会学,直到现在的文学艺术,都逐渐渗透了数学,逐步走上数学化的进程之中。
(一)数学与物理学
这几乎不用多说了。所有物理定律,都是由数学公式表达的。从天文、力学、光学、电磁学,直到原子物理,没有哪一科没有数学的支撑。而且,正是由于数学定理的发现,才催生出物理学的发现。如公元前3世纪古希腊数学家阿波罗尼斯(约前262—前190)在《圆锥曲线论》中给出关于圆锥曲线的理论及其性质,虽然此后很长一段历史时期没有发现它的应用,但却催生了欧洲中世纪关于天文学的新发现,并用圆锥曲线的理论和公式,来描述太阳系行星运动的规律。后来牛顿发明微积分,更从高等数学观点,严格证明了天体运行的规律。
太阳系中各大行星的轨道不同,运动周期不同,它们运行有什么规律呢?天文学家开普勒根据长期实际天文观测的数据,得出太阳系行星运动三大定律,其中第三定律的数学公式为: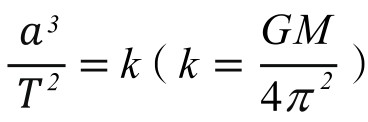 ,即绕以太阳为焦点的椭圆轨道运行的所有行星,其各自椭圆轨道半轴的立方与周期的平方之比是一个常量。它把非常复杂的太阳系各大行星运动秩序,说得多么地简单,多么地精妙!
,即绕以太阳为焦点的椭圆轨道运行的所有行星,其各自椭圆轨道半轴的立方与周期的平方之比是一个常量。它把非常复杂的太阳系各大行星运动秩序,说得多么地简单,多么地精妙!

图3-2-1 太阳系行星轨道运行图
牛顿的万有引力公式,则把宇宙中任意两个天体之间的相对运动规律,都给出数学说明。假设两个可以看作点的物体,各自质量分别为M与m,距离为r,那么二者之间的引力等于引力常数G乘以二者质量乘积除以距离平方。
即有如下公式(万有引力公式):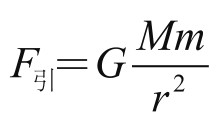
其中引力常数G约为6.67×10-11N · m2/kg2。
19世纪英国数学家和物理学家麦克斯韦(1831—1879)提出的电磁方程组的微分表达形式:
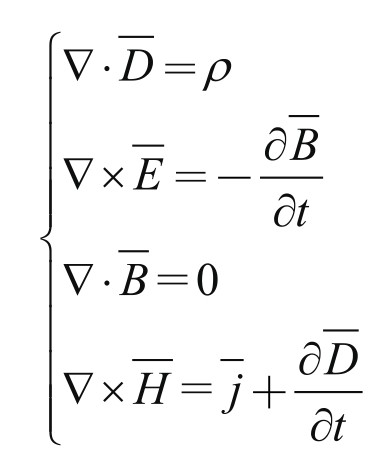
这一理论使人们认识到电与磁本质上都是波,建立了电与磁的相通性,阐释了电、磁与光一样都具有波动性,以及光的传播速度。这是数学与物理学典型的光辉结合而取得杰出成就的案例。其中算子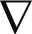 表示微分向量
表示微分向量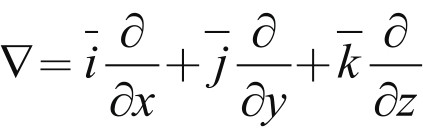 。
。
20世纪最杰出的科学成就,理应是电子计算机的发明和应用。而二进制计数法的发明,构筑了现代电子计算机算法语言的理论基础。电子计算机只能识别两个信号(电流的接通和断开),用1表示接通,用0表示断开。用二进制数码来进行编码,可编写出任意长的程序,进行计算和信息的传递。这才拉开了现代信息时代的大幕。
(二)数学与化学
化学研究物质的化学反应过程,以及物质的化学性质,离不开定量研究,这必然涉及计算。化学方程式,也借助数学公式的思想方法,进行推演和分析。
元素周期表,便是根据元素原子量大小进行排列的。各种原子结构、晶体对称形式与数学群论中对称群的计算结果一致。
最有意思的是,1996年获得诺贝尔化学奖的三位科学家,他们的贡献之一是发现了富勒烯。这是由60个碳原子组成的分子,这些碳原子连接成若干个正五边形和正六边形,类似于今天人们所见的足球形状,故又称其为“足球烯”(图3-2-2)。根据多面体欧拉公式V-E+F=2,可以计算得出其中正五边形有12个,正六边形有20个。这与足球表面形状一致。其中的数学道理,在后面第四章有一节专门讲述。
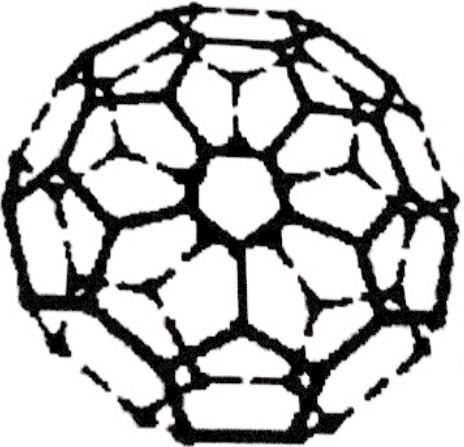
图3-2-2 足球烯
(三)数学与绘画
原始人类在狩猎与劳动中,与大自然亲密接触,引发他们对日月星辰、山川河流等大自然景物的崇拜,在部族中出现图腾崇拜,并刻画在山崖的壁画之中。东西方很多地方,都发现画有史前文化的壁画。古人们将他们的狩猎对象和自然景象,刻画在崖壁上,或山洞里,并从随意地刻画,到逐渐出现直线、圆、椭圆、三角形、菱形、长方形等几何图形。如西安半坡出土的距今五六千年的人面鱼纹彩陶盆就出现了方格图形等几何图形的刻画。
距今约4000年的大禹治水时期,已经有用于作图和测量的工具——规和矩。殷商时代的甲骨文中已经有“规”和“矩”二字。山东嘉祥县东汉石室(公元2世纪)中,有“伏羲手执规,女娲手执矩”的画像石(图3-2-3)。

图3-2-3 山东石室“规矩”画像石
自从黄金比例被发现之后,欧洲绘画与数学产生了更密切的关系。特别经过大艺术家达·芬奇大力提倡,人们将比例,特别是黄金比例广泛用于人体绘画中。他说:“美感完全建立在各部分之间神圣的比例关系上。”并详细指出人体各部分的比例。例如人体的肚脐位置,是全身的黄金点,人体各部分也都有一定的比例(图3-2-4)。
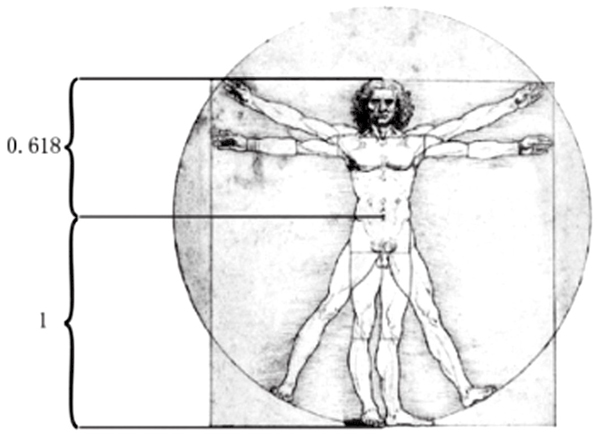
图3-2-4 人体绘画的黄金点
其后,德国人阿道夫·蔡辛在所著《人体比例的新理论》(1854年)中把黄金比例推崇为“打开自然和艺术形态构造之谜的金钥匙”。法国印象派画家舍勒特更是极力推崇黄金比例在绘画中的运用,以至他“用黄金分割原理来画出他的每一幅油画”。
现代计算机技术的发展,已经将数学与美术结合成一门新的学科——数学美术学。现在,计算机可以用简单的数学公式,经过千百次,以至上亿万次迭代,产生出电脑分形图画,复杂程度令人难以置信。而且人们可以将电脑绘画技术用于纺织印染、装潢设计等方面,大大增强了视觉效果,提高了艺术表现力。
以下,是由数学大师曼德尔布罗制作的若干分形图画(如图3-2-5所示),它们是通过数学公式进行迭代,由电脑自动生成的奇妙绘画作品。其奇妙如同梦幻,是人工所不能达到的。

图3-2-5 分形几何电脑图画
(四)数学与音乐
数学与音乐的关系,在中国古代就被十分重视。《史记·律书》中有对“律数”的相关记载,《汉书》以后的历代史书中,都把音乐与历数合编为《律历志》, “律”是指音律(音乐), “历”是指数学和历法。
相传黄帝派泠纶砍下昆仑山山阴(山的背阴处)之竹,取其竹节均匀的竹管一节,长9寸,直径3分(即其长度与直径之比为30∶1)。用此竹管吹出的音调,规定为标准音,名为“黄钟”,定其声音为“宫”【相当于现在的C调第一个音1(duo)】。
将此竹管长度定为81(等分),按照“三分损益”方法,得到十二个长短不同的竹管。用它们吹出音调,分别得到高低不同的“六吕”“六律”共十二个音调(构成一个完整的音程)。具体方法是:将黄钟(宫)竹管截去(损)三分之一,得到长54的竹管,用它吹出的音调定“林钟”(徵)。再将此竹管增加(益)三分之一,得到长72的竹管,吹出的音调,定为“太簇”(商)。继续损去三分之一,得到长48的竹管,吹出“南吕”(羽)。再三分益一,得到长64的竹管,吹出“姑洗”(角)。上述损益过程列表如下:
表3-2-1

但是,如此三分损益不是很准确,不能满足五声音阶的需要(中国古乐正是如此)。经过千余年的音乐实践,人们不断研究音程的科学划分。人们希望将其按比例分为12等份(对应12个半音),而使得高八度“宫”的频率恰好提高一倍(竹管则缩短一半)。怎么样才能做到呢?我国明代,朱氏皇族中出了个异类王子,数学家兼音乐理论家朱载堉(1536—1611),他解决了这个问题。他把一个音程按照比例分为12个半音,称为“十二平均律”,列表如下:
表3-2-2

欲使数列{ai}成等比数列,且a12=2a0。设其公比为q,则应有a12=q12a0,因此q12=2, q=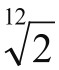 。此即是“十二平均律”,它是现代音乐的理论基础。这在当时是世界首创,比西方音乐理论家梅森(1588—1648)正式发表“十二平均律”(1636年)要早50年左右。
。此即是“十二平均律”,它是现代音乐的理论基础。这在当时是世界首创,比西方音乐理论家梅森(1588—1648)正式发表“十二平均律”(1636年)要早50年左右。
不仅如此,我国古代还利用黄钟竹管定音,制作铜编钟、石磬等乐器,以供祭祀礼仪使用。这还仅仅是黄钟定音制作乐器之用,此外还有“黄钟起度”的重要意义。因为有趣,不妨在这里介绍一下。
中国古代对于度量衡制度及其量器的标准的确定,是很重视的。因为,那时朝廷对民众收税,都是收取粮食布匹等实物,都要用度量衡标准量器来衡量物体的长短、容积和轻重。而量器的大小如何确定,对民众、对官府,都是一个重要的大问题。国家为了取信于民,想出一套制定度量衡标准量器的比较客观的办法,这便是“黄钟起度”的由来,而且记载于《汉书·律历志》上。“黄钟起度”的具体办法如下:
首先是长度单位。黄钟长度定为9寸。它的九分之一就是1寸,10寸为1尺,10尺为1丈。于是有了长度单位。
其次是体积单位。黄钟竹管的体积,定为1合,10合为1升,10升为1斗,10斗为1石(担)。
再次是重量单位。用籽粒均匀的粟(小米)1200粒,使其恰好装满一个黄钟竹筒,则其中粟的重量定为12铢,24铢为1两,16两为1斤(我国古代1斤16两制)。于是重量单位定下来了。
这样确定的度量衡单位有什么意义呢?我们知道,度量衡单位的大小,制定者可以随意规定,但其与百姓纳税交粮关系甚大,而朝廷为维护自身的公平性,要有个客观标准。但是以何为客观标准呢?怎么样才能让百姓相信呢?
黄钟竹管,就能给出一个客观标准。因为,用黄钟竹管定出的声音高低,已经用铜编钟记录下来,并被摆在庙堂之上。如果有谁不信,可以听听黄钟竹管吹出的声音,与铜编钟中的“宫”(黄钟)调声是否一致(以同频率声音的共振来判断)。于是,就用声音频率这种客观存在,保证了度量衡的竹管长度的可信度。
这样,就把原来可以由制定者随意决定的度量衡标准,建立在可以用铜编钟发出的声音(人人可以听到)加以鉴别的客观基础之上。这是多么奇妙的办法啊!
历史往往有鉴古观今的作用。我们今天和大多数国家所采用的长度单位——米(m),就是依据“黄钟起度”的科学原理制定的。
原来,各国采用公尺(m)为长度基本单位时,为保持标准一致,决定制作一个铂质原器——铂杆,以此杆两端之间的距离定为1m。于是,各国长度单位便有一个共同认可的标准实物(米原器)作标准。但是,它使用起来很不方便,同时难以保存使其维持不变。因此,1960年国际计量大会上,各国科学家决定:用同位素氪-86原子的2p10与5d5能级之间的跃迁所对应的辐射(光波)在真空中的1 650 763.73个光波的长度,来规定1米(m)的长度。
中国古代用声波频率来确定长度单位,现代用原子辐射光波的长度来确定长度单位,其间所依据的科学思想和科学原理,何其相似尔!
(五)数学与文学
数学与文学,本不同类,是相距很远的不同学科。数学是逻辑思维的产物,而文学主要是形象思维的产物。但是它们二者之间却有许多奇妙的联系。
其一,文学作品是社会的反映,其中必然牵涉到对人物和事物的描写,而无论人物还是事物,都有数量关系蕴含其中。作为文学作品的创作者,必须要做到“心中有数”。不然就会出问题,甚至是错误。前面已经举出过白居易的《琵琶行》和电视剧中“二楞妈”有关数字及计算的错误。以下再列举《红楼梦》中的有关情节予以说明。
例1.在《红楼梦》中,多次写到掷骰子的游戏。其中以第63回最为集中。
宝玉生日当晚,诸钗以掷四颗骰子为戏,看谁的点数多。每人轮流掷出的点数分别是:晴雯6点,宝钗16点,探春19点,黛玉18点,湘云9点,麝月10点,香菱6点。最后黛玉又掷出20点。这种情况合乎道理吗?
四颗骰子的点数,共有21种情况:从4点到24点。但每种情况出现的机会并不相同。为了研究方便,先研究两颗骰子的情况。两颗骰子点数的搭配,共有36种情况,由此可以计算出现各种点数的概率:我们用P(x)表示出现x点的概率,则有表3-2-3:
表3-2-3
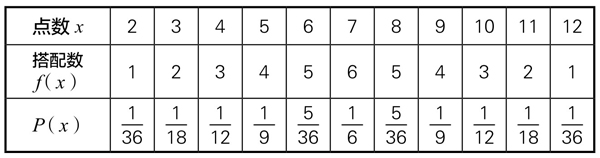
可见,掷两颗骰子出现7点的可能性最大,为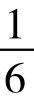 ≈16.7%;出现2点和12点的概率最小,为
≈16.7%;出现2点和12点的概率最小,为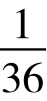 ≈2.78%
≈2.78%
那么,掷四颗骰子,哪种点数出现的可能性最大呢?
设想这四颗骰子分成两组,第一组点数搭配有36种,第二组点数搭配也有36种。所以这四颗骰子的所有点数,共有36×36=1296种不同的搭配。
现在来求当p=m+n(2≤m≤12, 2≤n≤12)时,四颗骰子点数的不同搭配数F(p)。怎样计算F(p)呢?现以计算F(10)为例作一说明。
我们这样来考虑:这10点是第一组m个点与第二组n个点之和:m+n,其中2≤m≤12, 2≤n≤12。那么,m与n搭配有以下7种情况:
m+n=10=2+8=3+7=4+6=5+5=6+4=7+3=8+2。
但对第一组m点来说,它是两颗骰子点数之和,又有f(m)种不同情况。第二组n点也有f(n)种不同情况。因此,按照加法原理和乘法原理,四颗骰子点数之和为10的所有不同搭配数为:
f(2)×f(8)+f(3)×f(7)+…+f(8)×f(2)
=2×(1×5+2×6+3×5)+4×4=80
因此,四颗骰子掷出10点的概率(根据对称原理亦即掷出18点的概率)等于P(10)=P(18)=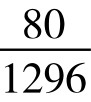 ≈6.17%。
≈6.17%。
用同样方法可以算出:
P(4)=P(24)=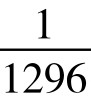 =0.08%;P(5)=P(23)=
=0.08%;P(5)=P(23)=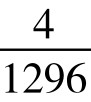 =0.3%;
=0.3%;
P(6)=P(22)=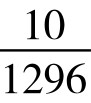 =0.8%;P(7)=P(21)=
=0.8%;P(7)=P(21)=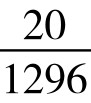 =1.6%;
=1.6%;
P(8)=P(20)=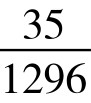 =2.7%;P(9)=P(19)=
=2.7%;P(9)=P(19)=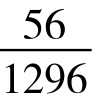 =4.3%;
=4.3%;
P(11)=P(17)=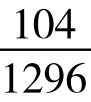 =8.0%;P(12)=P(16)=
=8.0%;P(12)=P(16)=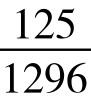 =9.6%;
=9.6%;
P(13)=P(15)=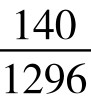 =10.8%;P(14)=
=10.8%;P(14)=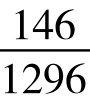 =11.3%。
=11.3%。
由此可见,一次掷四颗骰子出现14点的概率最大,约为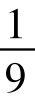 。其次为13点和15点,再次为12点和16点等等。而以4点和24点的概率最小,大约只有
。其次为13点和15点,再次为12点和16点等等。而以4点和24点的概率最小,大约只有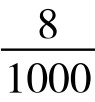 。
。
在《红楼梦》第63回掷四颗骰子的游戏中所出现的点数的概率,如表3-2-4所列:
表3-2-4

在这8次投掷中,概率最大的14点、13点、15点,都没有出现;反而概率极小的6点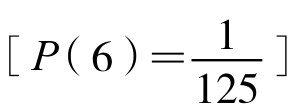 ,出现了两次。这是不合常理的。因为在投掷8次中出现两次6点的概率P8(6),按二项分布来计算,为
,出现了两次。这是不合常理的。因为在投掷8次中出现两次6点的概率P8(6),按二项分布来计算,为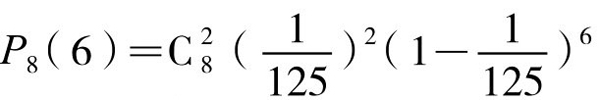 ≈0.001749(0.00175=0.175%)。这还不足
≈0.001749(0.00175=0.175%)。这还不足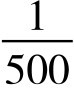 ,实在太小。也就是说,《红楼梦》所写的情况——投掷4颗骰子8次出现两次6点,几乎是不可能出现的。书中这么写,大概是因为作者对概率的无知。事实上,那时(18世纪)概率论才刚刚诞生,即使在欧洲也只有极少数人能够了解。如果曹雪芹现在还活着的话,他在再版时,一定会根据数学原理,来适当修改这段文字。
,实在太小。也就是说,《红楼梦》所写的情况——投掷4颗骰子8次出现两次6点,几乎是不可能出现的。书中这么写,大概是因为作者对概率的无知。事实上,那时(18世纪)概率论才刚刚诞生,即使在欧洲也只有极少数人能够了解。如果曹雪芹现在还活着的话,他在再版时,一定会根据数学原理,来适当修改这段文字。
例2.关于生日相同的问题。
在《红楼梦》中,大观园的一个小丫头发现:大观园里有好几个人的生日相同,觉得很奇怪。其实这很正常。因为大观园里有好几百人。两个人,或几个人的生日相同,一点也不奇怪。其实,在30人中有两人(或以上)生日相同的可能性,就大于二分之一。
在30人中有两人生日相同的机会究竟有多大呢?我们来计算一下。
我们可以先从反面考虑:计算在30人中,没有人生日相同的可能性。
以平年365天计算,每个人出生在哪天,完全是随机的。就像把所有的日期装在一个大袋子里,随便从中摸出一个。那有多少种可能呢?——365种。因此第一个人的生日,有365种可能情况。如果没有生日相同,第二个人的生日,就只有364种可能情况了。第三个人呢?——363种;第四个人——362种;……;第三十个人——只有336种了。于是,30人中没有人生日相同的情况,总共有365×364×363×…×336种情况,而总的可能情况则有36530种。因此,在30人中没有任何两人生日相同的可能性,应为
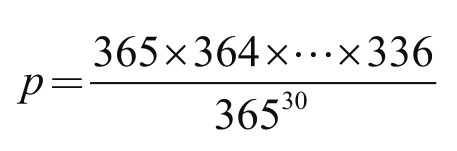
用计算器算一算,不难算出它的值来:
这个分式的近似值为p=0.2936837…≈0.29。
——那么,30人中有人生日相同的可能性是多少呢?
当然是1-p≈0.71。就是说,30人中有两人或者更多的人生日相同的可能性,在70%以上。
例3.在我国清代的一部小说《镜花缘》中,第93回有“米兰芬妙算灯球”一事,含有数学的妙趣,历来为人们所欣赏。故事说的是,众才女在宗伯府观灯,灯上都挂着灯球。楼下的灯球有两种形状,一种是大球下缀2个小球,另一种是大球下缀4个小球,共有大球360个、小球1200个。楼上的灯球也有两种,一种是3个大球下缀6个小球,9个球结为一灯;另一种是3个大球下缀18个小球,21个球结为一灯。共有大球396个、小球1440个。问楼上楼下各有多少盏彩灯?
这是一个有趣的数学问题。米兰芬不愧为“持筹才女”,她不慌不忙,默算一回,便给出答案:楼下360盏彩灯,楼上132盏彩灯。
她是怎么算的呢?她说:楼下彩灯,只按照鸡兔同笼的算法:大球下缀2个小球的当作鸡,下缀4个小球的作为兔,于是按照中国古算中鸡兔同笼算法,便知:半足,减头数,得兔数目(大球下缀4小球者);头数减兔数,得鸡数(大球下缀2小球者)。即1200÷2=600, 600-360=240(兔数), 360-240=120(鸡数)二者相加得240+120=360,为楼下彩灯数。
楼上彩灯数,计算复杂一些,要用代数解方程组。设两种彩灯数目分别为x, y个,则有方程组:
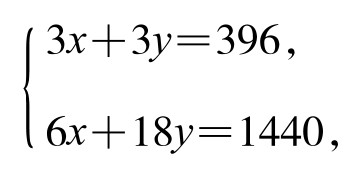
解得x=78, y=54, x+y=132。
由于数学问题及其算法,掺入了小说,遂使小说增加了思维的趣味。
其二,文学作品中的语言其实有规律可循。人们说话或写成文字的书面语言,都各有特点,这种特点可以用某些特定的语词或字的分布频率,来加以刻画。即可以使用数学统计的方法,来描述和刻画每个人语言(包括书面语言)的特点。
这样做有什么作用呢?可以对文稿进行作者鉴别。现以《红楼梦》为例。该书作者究竟是谁,历来是“红学”一个悬而未决的考证问题。
社会上提出过种种猜测,有认为全书作者为曹雪芹一人的,也有认为《红楼梦》前八十回的作者是曹雪芹,后四十回为高鹗所续。但是至今仍无公认的结论。然而,若用数学统计方法——语言统计学来研究,可以提供新的思路和理论支持。
前有一位赵冈先生,取《红楼梦》书中“儿”“在”“事”“的”“著”五个字作为样本,对《红楼梦》前八十回和后四十回,分别进行统计。计算它们的分布频率、标准差和变异系数。结果表明:《红楼梦》前八十回与后四十回的数据,竟然大体一致,没有多大的差别。于是他做出初步判断:《红楼梦》前八十回和后四十回的作者,应该是同一个人。即使是出于两人之手,这二人的文字笔法也基本相同。
其后,复旦大学李贤平先生认为,赵先生只用五个字作样本,体量太小,不足以反映真实情况。于是他增大样本量,选取47个虚词——“之”“其”“方”“于”等文言虚词,“呀”“吗”等句尾虚词和“了”“的”“着”“一”“不”等白话虚词作样本,用多种统计方法来进行计算和分析,发现《红楼梦》的前八十回和后四十回,在文字和笔法上有所交叉。他得出的结论是:全书由一人(曹雪芹)执笔,中间由别人插写了第6~16回“风月宝镜”和第63~66回情节,创作出元妃省亲,扩建大观园,为宝玉和诸钗提供了广阔的活动空间。经过几次增删,原来计划仅写110回,曹雪芹在最后一次修改中,增加了某些神话色彩,使全书扩成120回。但可能由于曹雪芹早逝,前八十回才完稿,后四十回未定稿,而由其亲友整理成现在的书稿。
这些论述,曾经在红学界引起不小的轰动。当然,这仅是用数学(统计学)方法研究语言的成果之一,是否被广大红学界人士认可,当是另外的问题。无论如何,用数学统计方法研究语言学,给语言和文学界提供了一种新的定量研究方法,比一般定性研究,有较多的可靠性。这不能不说是数学与文学的一种美妙结合。
(六)数学与诗联(https://www.daowen.com)
数字入诗,古已有之。如唐诗名句:“飞流直下三千尺,疑是银河落九天”(李白《望庐山瀑布》);“两个黄鹂鸣翠柳,一行白鹭上青天”(杜甫《绝句》);“千山鸟飞绝,万径人踪灭。孤舟蓑笠翁,独钓寒江雪”(柳宗元《江雪》),句句都有数字,或“准数字”(如两、孤、独)。
数字入诗有好处吗?能够增加诗词的美感吗?当然如此。
第一,数字的确切性、准确性,给诗词增加了明快和亮丽的语言色彩,增加了联句的力量。
第二,数字具有极大的概括性,诗词又极其凝练,可以在字数很少的诗句中,包容很大的空间和思想内涵。
第三,数字的音韵铿锵,可以增加诗句的声韵美。
第四,数字有利于诗联对仗的要求。在古典诗词中,很多句式要求对仗。即名词对名词,动词对动词,虚词对虚词。而数字入诗,可以提高对仗的准确性——数字(词)对数字(词)。这方面的例子很多。
例1.李白诗句:
一叫一回肠一断,三春三月忆三巴。
这是李白晚年在安徽宣城,听到杜鹃鸟的叫声,而联想到他的故乡四川“三巴”时的即兴之作。
例2.清代才子纪晓岚一次陪同乾隆帝在江边赏景,眼前出现一个渔翁划一条小渔船在江中打鱼。乾隆帝命纪晓岚即时赋诗,但要求含有十个“一”字。以下就是纪晓岚所作的数字诗:
一篙一橹一渔舟,一个艄公一钓钩。
一拍一呼还一笑,一人独占一江秋。
诗歌中十个“一”字,各得其所,并不觉得重复和繁杂,反而觉得轻灵而有妙趣。
例3.郑板桥《咏雪》:
一片两片三四片,五六七八九十片。
千片万片无数片,飞入芦花看不见。
这首咏雪诗,把从下雪之初,到漫天大雪的全过程,都写了出来。虽然用了许多数字,却并不显得重复,反而生动而有趣。后来电视剧《宰相刘罗锅》将其写入其中,加在了刘罗锅的头上。
数字对仗除了运用在诗联之中,我们还经常在对联中看到。
对联,是我国传统文学最简单的形式之一,只有上下两句,文字要求对仗工整,富有文学品位和思想内涵。而数字的嵌入,可以为字数很少的对联,大大增加内涵、扩大视野,又容易满足对仗工整的要求。
传统春联,如:
一元复始,万象更新;
一夜连双岁,五更分二年;
生意兴隆通四海,财源茂盛达三江;
八骏西来腾紫气,三阳开泰耀金辉(甲午年);
…………
名胜联,如:
例1.江苏淮阴侯祠对联:
生死一知己,存亡两妇人。
上下联短短十个字,却总结了汉代名将韩信的一生。上联中的“一知己”指的是“萧何”。韩信是萧何向汉王刘邦极力推荐的,是“萧何月下追韩信”追回来的。而汉朝建立以后,又是萧何设计将韩信骗入宫中,使韩信被吕后以谋反罪名杀害。所以后来有成语“成也萧何,败也萧何”。
下联说的是,在韩信早年落难时,幸得妇人漂母接济,才得以生存。而其后又是被另一妇人吕后杀害。韩信一生一死,一存一亡,尽在这副对联之中。而其中数字一和两(二),起了点睛和高度概括的作用。
例2.湖北隆中三顾堂对联:
两表酬三顾,一对足千秋。
《三国演义》中三顾茅庐的故事,广为流传。三顾堂是刘备三顾茅庐、诸葛亮作隆中对时的纪念堂,门口这一联,既点明了刘备三顾茅庐的故事,也概括了诸葛亮一生对刘备的衷心和历史功绩。上联中“两表”指诸葛亮前出师表和后出师表。下联中“一对”指的是诸葛亮与刘备的对话,给刘备指出天下大势,略作三分的战略纲领。两联十个字,把刘备“三顾茅庐”“隆中对”和诸葛亮的前后出师表,都以严整的对联写尽。
例3.山东济南大明湖联:
四面荷花三面柳,一城山色半城湖。
大明湖正好位于济南城市中心,湖中遍植荷花,环湖则三面柳树,还有一面是市政建筑并正好面对千佛山的美丽山色。此联恰到好处地刻画出济南以大明湖为中心的山光水色。
例4.安徽采石矶太白楼联之一:
携八百里洞庭,拄杖来游,万里长江奔眼底;
邀一千年明月,举杯酹酒,几多往事上心头。
据说此联为清代重臣曾国藩,在镇压太平天国后,怀着复杂心情,从湖南出发顺江而下,路经采石矶登太白楼时所书。上下联都嵌入数字,对仗工整,气势不凡,而又浮想联翩。上联写出作者从湖南洞庭湖而来,经万里长江来游的历程;下联写作者登楼时,对千年前的太白诗仙敬仰的心情,以及对往事的感叹。
例5.昆明大观楼长联:
五百里滇池,奔来眼底,披襟岸帻,喜茫茫空阔无边。看东骧神骏,西翥灵仪,北走蜿蜒,南翔缟素。高人韵士,何妨选胜登临,趁蟹屿螺洲,梳裹就风鬟雾鬓;更苹天苇地,点缀些翠羽丹霞。莫辜负四围香稻,万顷晴沙,九夏芙蓉,三春杨柳。
数千年往事,注到心头,把酒凌虚,叹滚滚英雄谁在?想汉习楼船,唐标铁柱,宋挥玉斧,元跨革囊。伟烈丰功,费尽移山心力。尽珠帘画栋,卷不及暮雨朝云;便断碣残碑,都付与苍烟落照。只赢得几杵疏钟,半江渔火,两行秋雁,一枕清霜。
这副著名长联,上下联各嵌入五个数字(准数字),使得对联的概括性大大增强,视野大大扩展,而文字却显得更加凝练。
此外,在日常生活中,流传着很多含数字的名言,例如:
为山九仞,功亏一篑。——《书经》
文武之道,一张一弛。——《礼记·杂记下》
一叶障目,不见泰山。两耳塞豆,不闻雷霆。——《鹖冠子》
放之四海而皆准。——《礼记》
一言而兴邦,一言而丧邦。——《论语》
益者三友,损者三友。友直,友谅,友多闻,益矣。友便辟,友善柔,友便佞,损矣。——《论语》
君子有三畏:畏天命,畏大人,畏圣人之言。——《论语》
三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩。——《论语》
三人行,必有我师焉。——《论语》
三军可夺帅也,匹夫不可夺志也。——《论语》
子在齐闻《韶》,三月不知肉味。——《论语》
彼一是非,此一是非。——《庄子·齐物论》
九层之台,起于累土。千里之行,始于足下。——《道德经》
十年树木,百年树人。——《管子》
千丈之堤,以蝼蚁之穴溃;百尺之室,以突隙之烟焚。——《韩非子》
不以一眚掩大德。——《左传》
圣人千虑,必有一失;愚人千虑,必有一得。——《晏子春秋》
百川东到海,何时复西归?少壮不努力,老大徒伤悲。——汉乐府《长歌行》
不飞则已,一飞冲天;不鸣则已,一鸣惊人。——《史记》
差之毫厘,谬以千里。——朱熹《四书章句集注》
吃一堑,长一智。——王阳明《与薛尚谦书》
会当凌绝顶,一览众山小。——杜甫《望岳》
忽如一夜春风来,千树万树梨花开。——岑参《白雪歌送武判官归京》
三更灯火五更鸡,正是男儿发愤时。——颜真卿《劝学》
试玉要烧三日满,辨材须待七年期。——白居易《放言》
谁言寸草心,报得三春晖。——孟郊《游子吟》
春风得意马蹄疾,一日看尽长安花。——孟郊《登科后》
春色满园关不住,一枝红杏出墙来。——叶绍翁《游园不值》
春宵一刻值千金。——苏轼《春宵》
但愿人长久,千里共婵娟。——苏轼《水调歌头》
读万卷书,行万里路。——董其昌《画禅室随笔》
含有数字的成语,则更多,略举一些常用成语如下:
一来一往、一来二去、接二连三、不三不四、三从四德、四舍五入、五颜六色、七上八下、八九不离十、十拿九稳、百里挑一、千奇百怪、千言万语、万无一失、亿万斯年、百闻不如一见等等。
在我国古算书中,还有以诗词形式写成的数学题和解题算法,略举几例:
例1.“孙子歌”。
中国古算书《孙子算经》中有一个著名的“孙子问题”:有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
这实际上是个一次同余式组问题。《孙子算经》中只给出了求解的关键步骤和答案。南宋数学家秦九韶给出求解的一般算法“大衍求一术”和“大衍总数术”。按此方法,其程序是:
3——70(被5、7除尽,而被3除余1);
5——21(被3、7除尽,被5除余1);
7——15(被3、5除尽,被7除余1)。
将对应三数的倍数相加:70×2+21×3+15×2=233。
再减去105(3, 5, 7之积)的若干倍,得最小正整数。
而233-105×2=23,即本问题的最小正整数解。
后来人们根据秦氏的以上算法,总结出一首“孙子歌”:
三人同行七十稀,五树梅花廿一枝。
七子团圆正月半,除百零五便得知。
这“孙子歌”实际上就是一首七言绝句。
例2.明代数学家、珠算大师程大位所著《算法统宗》,集珠算之大成。其中的数学题目及其算法,很多都是采用诗词体写出来的。如书的开篇《先贤格言·改调西江月》写道:
智慧童蒙易晓,愚顽皓首难闻。世间六艺任纷纷,算乃人之根本。
知书不知算法,如临暗室昏昏。谩同高手细评论,数澈无劳方寸。
关于“九因”(珠算九九乘法),则写成七言绝句加以概括:
合数九因须记熟,起手须从末位推。
言十就身如隔位,若要还原用九归。
关于“九归”(珠算除法),写成如下绝句:
学者如何用九归,先从实上左头推。
逢进起身须进位,下加次位以施为。
