最佳运输方案的制定
八、最佳运输方案的制定
问题:A、B、C三个城市分别有某种机器10台、10台和8台,D、E两市则分别需要这种机器18台和10台,从A市运1台机器到D、E的运费,分别为200元和800元;从B市运1台机器到D、E的运费,分别为300元和700元;从C市运1台机器到D、E的运费,分别为400元和500元。则:如何安排运输,使总的运费最少?
分析:问题中的数据很多,我们可以设计出一张表格,将这些数据分类列于表中,使我们能看出其间的关系(表4-8-1):
表4-8-1
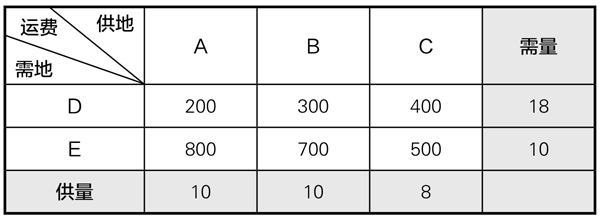
如果从A市运x台机器到D市,从B市运y台机器到D市,能够满足问题的要求,那么,有关两个城市之间的运费,就如表4-8-2所示:
表4-8-2
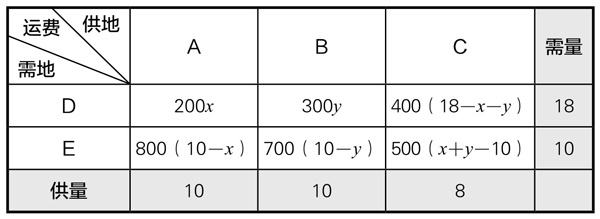
从表4-8-2可见:
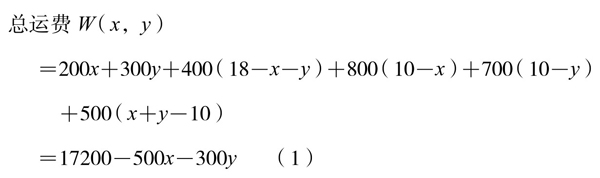
其中x、y的限制条件是:
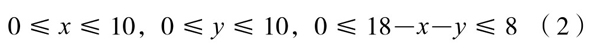
于是,我们的问题就是:在条件(2)的约束下,求函数(1)的最小值。
函数(1)称为目标函数,(2)为限制条件。这里的目标函数是线性函数,这就是一个线性规划问题。
问题求解:对于这个特殊的目标函数(1),可以变形如下:
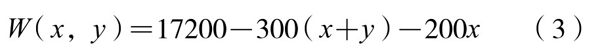
因为由条件可得10≤x+y≤18,而当x+y=18时,x的最大值为10,所以将x+y=18, x=10(y=8)代入(3),得W的最小值W(10,8)=9800(元)。
线性规划问题的典型提法是:求目标函数(二元线性函数)
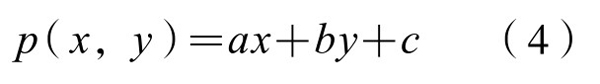
在一组线性不等式
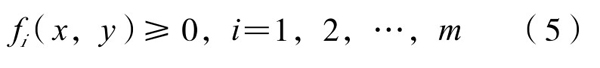
的限制下的最大值或最小值。
解决线性规划问题,通常有三种方法:表上作业法、图上作业法和多边形法。
现在就以上面的问题为例,分别介绍这三种方法。
(一)表上作业法
已如上述:设计和绘制表格,将相关数据填入表中(如表4-8-1)。
在表中,对D地供货的A、B、C三地中,首先选运费最少的A地,尽可能地先从A调运10台到D地;不足的8台,再从运费次少的B地调运。此时,对E地可以供货的,只有B、C两地,而其中B地只有2台可调运,其余8台从C地调运。这样就得到一个合理的调运方案。此时,如我们已经做过的,其总运费的最小值为W(10,8)=9800元。
(二)图上作业法
如果将表4-8-1中两地之间的运费,看作两地之间的距离(距离与运费成正比),那么目标函数W(x, y)就是总的运量。以点代表各地,按照两地的距离长短,按比例画出连接线段,画一个运输路线图——加权图(图4-8-1),把问题表示出来:
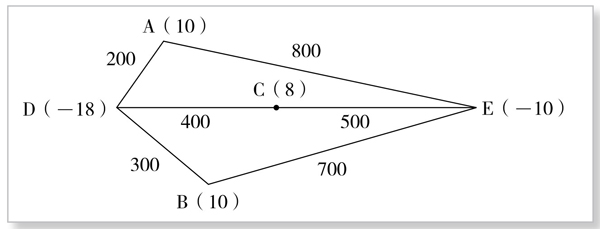
图4-8-1
图中供地A、B、C的供量,用正数表示;需地D、E的需量,用负数表示。
制定运输方案时,在图上进行作业:在连接需地D的三条路线中,先从最短路线AD运入10台;再从次短路线BD运入8台。运输路线用箭头表示。对需地E,从C地运入8台,从B地运入2台。从而得到一张运输流程图(图4-8-2):
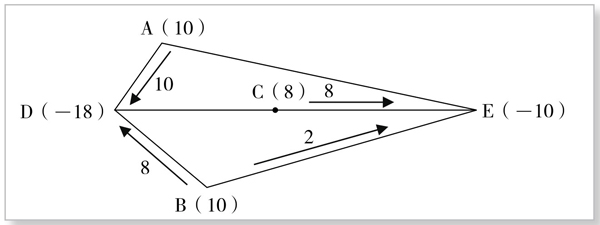
图4-8-2
按此图安排运输,其结果与表上作业法一致,只是将运费换成了运程。计算可得其总运费的最小值为W(10,8)=9800元。
(三)多边形法
在x-y平面上,目标函数(4)表示一组平行直线,限制条件(5)一般表示一个多边形。例如,本例中的限制条件0≤x≤10, 0≤y≤10, 0≤18-x-y≤8就表示一个等腰梯形,如图4-8-3所示的阴影区域G。
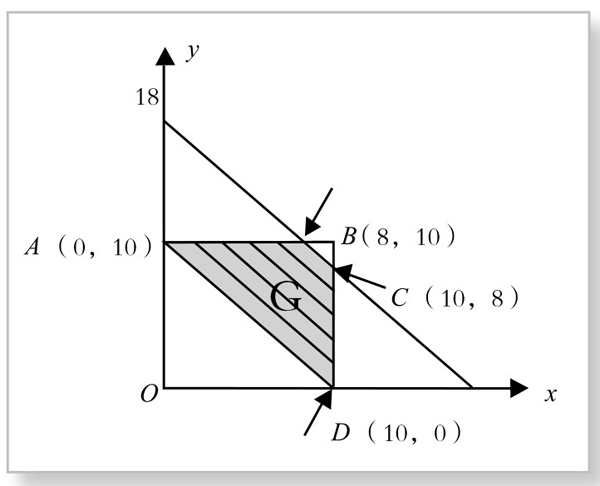
图4-8-3
而目标函数W(x, y)=17200-500x-300y是一组平行直线。W(x, y)的最大或最小值,一定经过这个多边形的顶点。因此,只要计算得此多边形顶点的坐标,并代入直线方程,其中最大值或最小值,就是我们所要求的结果。
经过计算,区域G的顶点坐标为:A(0,10), B(8,10), C(10,8), D(10, 0)。
由此得W(x, y)的最小值和最大值分别是:minW=W(B)=9800, maxW=W(A)=14200。
三种解法,各有其妙,各有其美。
