析取和否定规则
2.1 特殊析取规则
如果析取肢p和q是相斥的,析取p∨q的概率便能够用特殊析取规则由它的析取肢的概率计算出来。
规则4: 如果p和q是相斥的,那么
P(p∨q) =P(p) +P(q)
例: “苏格拉底既秃头又聪明”和苏格拉底既不秃头也不聪明”是相斥的,如果前一陈述的概率是二分之一,而后一陈述的概率是四分之一,那么“或者苏格拉底既秃头又聪明或者苏格拉底既不秃头也不聪明”的概率便是二分之一加四分之一,即四分之三。
假定你将要投掷一个有六个面的骰子,每一面出现的概率是相等的,就是说:


因为每次投掷这骰子只能露出一面,可以把这六个陈述看作互相排斥的。这样我们便可以根据特殊析取规则计算出得到“1”或“6”的概率,如下:
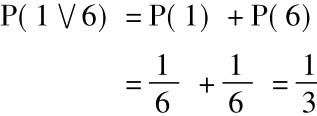
得到一个偶数的概率可以这样计算:
P(偶数) =P(2∨4∨6)
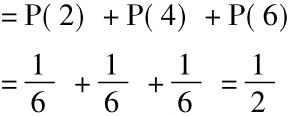
得到一个大于“3”的偶数的概率可以这样计算:
P(大于3的偶数) =P(4∨6)
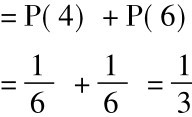
得到一个偶数或“3”的概率可以这样计算:
P(偶数或3) =P(2∨4∨6∨3)
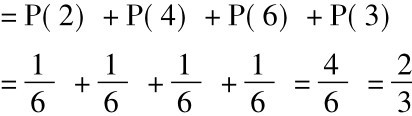
最后,得到或者“1”或“2”或“3”或“4”或“5”或“6”的概率(就是说这骰子将露出这一面或那一面的概率)是六分之六或一。
现在我们把特殊析取规则应用于一个有更广泛兴趣的事例。因为任何陈述p和它的否定~p都是相斥的,按照特殊析取规则得:
P(p∨~p) =P(p) +P( ~p)。但陈述p∨~p是重言式,所以根据规则1,
P(p∨~p) =1
把这两个结论合起来便得:
P(p) +P( ~p) =1
如果从方程式都减去P(p),这两边仍相等,所以我们可以作出结论:
P( ~p) =1-P(p)
这个结论对任何陈述都有效,因为任何陈述都与其否定相矛盾,并且对于任何陈述p,p与其否定的析取p∨~p是一个重言式。这就确立了一个普遍否定规则,它使我们能够由一个否定的成分陈述的概率去算出这个否定的概率:
规则5: P( ~p) =1-P(p)(https://www.daowen.com)
假定在关于骰子的例中我们要知道得不到“3”的概率:
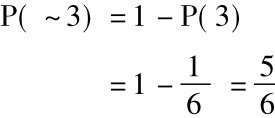
我们如果只能够用特殊析取规则,通过较长的计算来解决问题,也得到相同的答案:
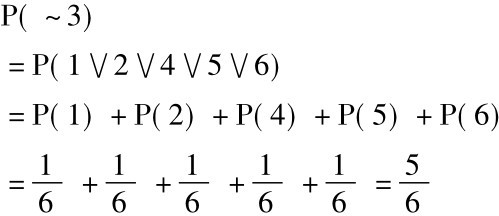
2.2 普遍析取规则
现在我们再一次应用特殊析取规则,以便确立另一个有用的普遍规则。对于任何两个陈述p和q,我们知道复合陈述p∧q,p∧~q,和~p∧q是互不相容的。因此,我们能够应用特殊析取规则得出,
a. P[(p∧q)∨(p∧~q)]
=P[(p∧q) +P(p∧~q)]
b. P[(p∧q)∨( ~p∧q)]
=P(p∧q) +P( ~p∧q)
c. P[(p∧q)∨(p∧~q)∨( ~p∧q)]
=P(p∧q) +P(p∧~q) +P( ~p∧q)
但复合陈述(p∧q)∨(p∧~q)逻辑地等值于简单陈述p。因为按照规则3,逻辑地等值的陈述有相同概率,方程式(a)可以改写为
a'.P(p) =P(p∧q) +P(p∧~q)
同理,复合陈述(p∧q)∨( ~p∧q)逻辑地等值于简单陈述q。所以方程式(b)也可以改写为
b'.P(q) =P(p∧q) +P( ~p∧q)
最后,复合陈述(p∧q)∨(p∧~q)∨( ~p∧q)逻辑等值于复合陈述p∨q,这使我们能够把方程式(c)改写为
c'. P(p∨q)
=P(p∧q) +P(p∧~q) +P( ~p∧q)
让我们把方程式(a')和(b')相加便得
d'. P(p) +P(q)
=2P(p∧q) +P(p∧~q) +P( ~p∧q)
把方程式(d')和方程式(c')比较一下便会看到,P(p∨q)和P(p) +P(q) -P(p∧q)都和同一个东西相等,这就确立了一个普遍析取规则,它对每一个析取都适用,不管它的析取肢是否互相排斥。
规则6: P(p∨q)
=P(p) +P(q) -P(p∧q)。
假定我们要知骰子将露出偶数或一个小于“3”的数的概率,用特殊析取规则是这样计算的:
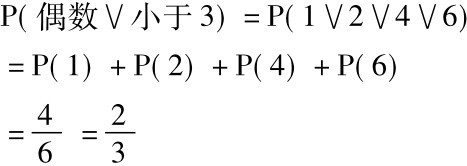
因为结果“1”、“2”、“3”、“4”和“6”是互相排斥的,我们可以用特殊析取规则。但是,结果“偶数”和“小于3”并不是互相排斥的,因为骰子可以露出“2”。像这样,我们可以应用普遍析取规则如下:
P(偶数∨小于3)
=P(偶数) +P(小于3) -P(偶数∧小于3)
根据特殊析取规则,我们计算出P(偶数)即P(2∨4∨6)等于二分之一。我们也根据特殊析取规则算出P(小于3)即P(1∨2)等于三分之一。我们还算出P(偶数∧小于3),即P(2)等于六分之一。所以,我们用这个方法得:
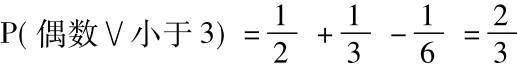
在这个例中可以清楚地看到减去项的作用。我们的做法是把P(偶数∨小于3)计算为
P(2∨4∨6) +P(1∨2) -P(2)
这样,在我们把P(偶数)和P(小于3)相加时,P(2)被加入两次,减去项校正了这一点。在这个例子中,用普遍析取规则来解题是很麻烦的。但有些事例必须使用普遍析取规则。假定别人告诉你:
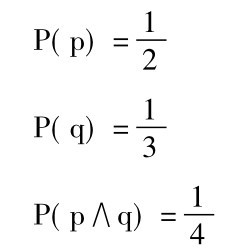
请你计算P(p∨q)。现在你不能够使用特殊析取规则,因为你知道p和q不是互相排斥的。如果它们互相排斥,P(p∧q)就会等于零,而别人告诉你是四分之一。所以你必须以如下方式使用普遍析取规则:
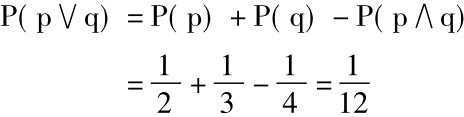
概率演算和真值表方法的相似是受限制的。如果我们知道一个复合陈述的简单成分陈述是真的或者假的,我们便永远能够决定这个复合陈述的真或假。但我们却不是永远能够由简单成分陈述的概率去算出一个复合陈述的概率。有时如上例,要算出复合陈述p∨q的概率,我们不仅需要知道它的简单成分陈述p和q的概率,还需要知道另一个复合陈述p∧q的概率。在下一节我们将要讨论决定这种合取的概率的规则。但是,我们将会发现,并不永远能够简单地由其成分陈述的概率去算出一个合取的概率。
