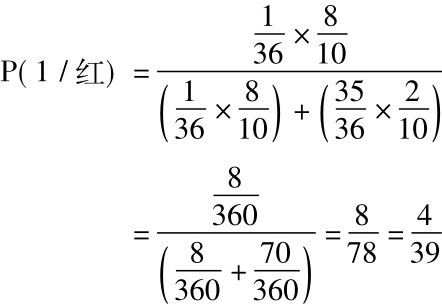合取规则和条件概率
3.1 条件概率
条件概率是对一对陈述q、P(或h、e)的测度,写作P(q/p),读作“以p为条件的q的概率(或‘q给定p’的概率)”。相对于条件概率来说,P(q)和P(p)便叫做q和p的初始概率或先验概率。条件概率可和先验概率相同或不同。投掷骰子的例子中,投掷一个偶数的概率是二分之一,但是给定“2”或“4”已出来,得到一个偶数的概率便不是二分之一而是一,而给定已出来的是“1”或“3”,得到一个偶数的概率便是零。下面给定三个不同的条件,“偶数”的概率都和“偶数”本身的概率不同:

条件概率考虑到这个事实: 如果一定陈述p被知是真的,这就会影响给另一陈述q分配的概率。最明显的例子出现在由p到q的论证是演绎地正确的时候:

在这种情况下:
P(q/p) =1
P(偶数/2∨4) =1
但在许多重要情况下,由p到q或由p到~q的论证不是演绎地正确的,而P(q/p)不同于P(q),如上例。
如果P(q/p) =P(q): 陈述q和陈述p便是概率地(或统计地)独立的(independent)。就是说,知道p是真的同分配给q的概率一点也不相干。换一个相等的说法,q独立于p又可以定义为P(q∧p) =P(p)p(q)。这样,概率独立性是对称的: 如果q是概率地独立于p,那么p便是概率地独立于q,对一切q和p都成立。
如果q和p不是概率地独立的,那么在q和p之间就存在概率的(或统计的)相关(correlation)。这是正相关还是负相关,随P(q/p)是大于或小于P(q)而定。这种情况有时被这样地描述: p对于q是概率地正相干(positivelyrelevant)或负相干的(negtivelyrelevant)。
请注意下面六个概率陈述是等值的:
P(q) <p(q/p);
P(p) <P(p/q);
P(q/~p) <P(q);
P(p/~q) <P(p);
P(q/~p) <P(q/p);
P(p/~q) <P(p/q)。
并且如果所有的“<”号都改为“>”号或“=”号,这些陈述也是等值的。这样,这两种概率相关(正的和负的)以及概率独立性都是对称的,如果P(q/r∧p) =P(q/r),我们便说陈述r遮掩掉(screenoff)q和p之间的任何概率相关。
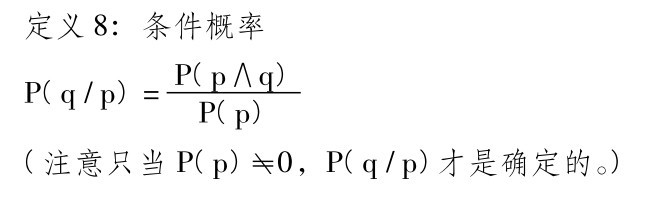
让我们看看在掷骰子的例子中,这个定义怎样被证明是有效的:
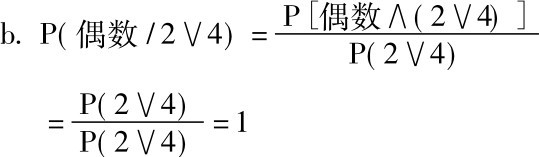

3.2 合取规则
对任何q和p来说,上述条件概率定义的一个直接推断便是普遍合取规则。
规则7: P(p∧q) =P(p) ×∧(q/p) =P(q) ×P(p/q)
证明是很简单的。用条件概率定义:
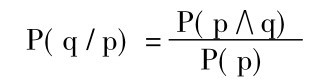
以P(p)乘方程两边得:
P(p) ×P(q/p) =P(p∧q)
因为当p独立于q时,P(q/p) =P(q),在普遍合取规则中我们可以用P(q)代替P(q/p),便得:
P(p) ×P(q) =P(p∧q)
这个结果构成特殊合取规则:
规则8: 如果p和q是独立的,那么
P(p∧q) =P(p) ×P(q)
普通合取规则比较起来更为基本,但特殊合取规则较简单,让我们先举例说明它的应用。假定同时投掷两个骰子,基本的概率如下:
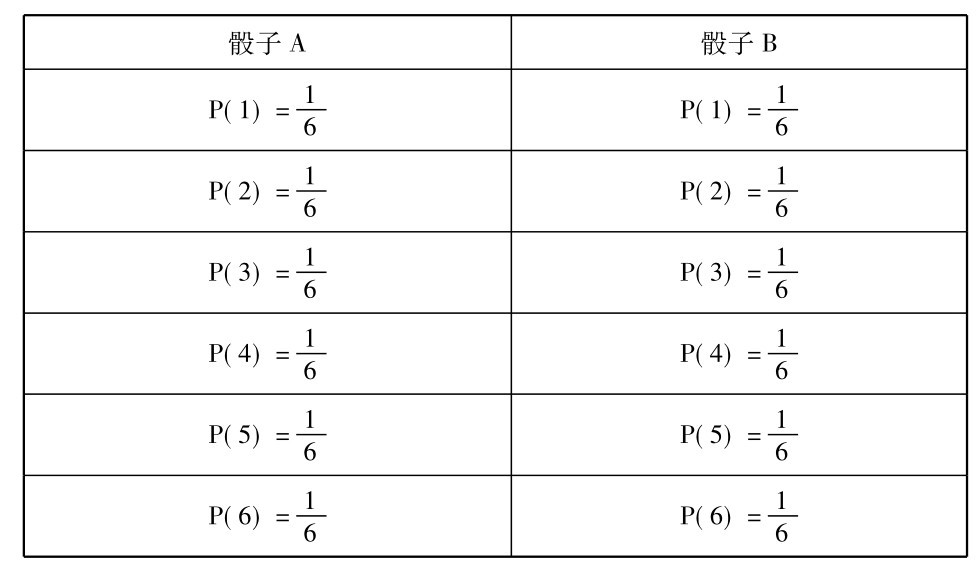
因为骰子A露出的那一边并不会影响骰子B露出的那一边,反过来也是一样,断定A的各种不同结果的陈述对于断定B的各种不同结果的陈述是独立的。例如,“骰子A将露出3”和“骰子B将露出5”是互相独立的。所以,假定我们要知道A得“1”而B得“6”的概率便可用特殊合取规则:
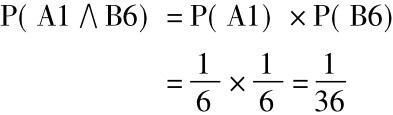
另一个例: 要知道骰子得出“1”和“6”的概率,有两种可能配合: A得“1”而B得“6”,或B得“1”而A得“6”。
P(1∧6)
=P[(A得1∧B得6)∨(B得1∧A得6)](https://www.daowen.com)
用特殊析取规则得
P[(A1∧B6)∨(B1∧A6)]
=P(A1∧B6) +P(B1∧A6)
用特殊合取规则已经算出
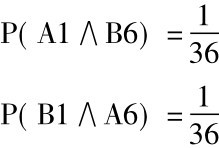
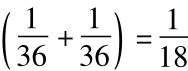
当两个陈述不是独立的,我们便应用普遍合取规则,如下例: 假如别人交给你一个口袋,里面装有十颗胶姆糖,五颗红的,五颗白的。你要摇匀这个口袋,闭上眼睛,取出一颗糖,看一看吃了它,然后重复这个过程。我们将假设在每次取糖时,袋中每一颗胶姆糖都有被取出的相等概率。问题是寻求取出两颗红色胶姆糖的概率。
要解答这个问题,我们必须寻找合取P[(1次取红∧2次取红)]——下面将简写作P(红1∧红2)的概率。我们首先求P(红1),我们将用一个字母来标示每一颗糖: A,B,C,D,E,F,G,H, I,J。我们知道在头一次取糖时我们将取出其中的一颗,所以
P(A1∨B1∨C1∨……J1) =1
根据特殊析取规则,
P(A1) +P(B1) +P(C1) +……P(J1) =1
因为每一颗糖都有同等机会被取出,并且共有十颗糖,所以
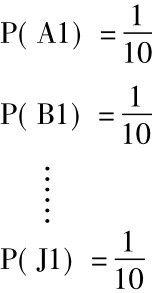
我们说过有五颗红糖,我们将用A、B、C、D、E来标示红糖,用其余字母标示白糖。根据特殊析取规则,第一次取糖得到一颗红糖的概率是:
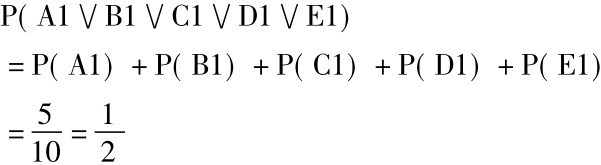
我们将必须用普遍合取规则去寻求P(红1∧红2),因为“第一次将取出红糖”和“第二次将取出红糖”这两个陈述不是独立的。如果第一次取出了红糖,袋中剩下四颗红的和五颗白的,在第二次都有同等机会被取出。但如果第一次取出了白糖,就剩下五颗红的和四颗白的等侯第二次被取出。所以知道第一次取出了红糖就会影响我们给第二次取出红糖所分配的概率,这两个陈述不是独立的,我们应用普遍合取规则得:
P(红1∧红2) =P(红1) ×P(红2/红1)
我们已经找到了P(红1)。现在我们必须算出P(红2/红1)。假定我们第一次取出了红糖,便剩下九颗糖,四颗红的和五颗白的。我们必须取出其中之一,而它们都有同等机会被取出。根据类似上面所用的推理,每颗都有九分之一的概率被取出,而取出一颗红糖的概率是九分之四。所以
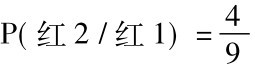
现在可以完成我们的计算了:
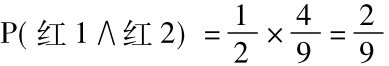
我们能够以相同方式算出P(白1∧红2)
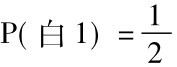
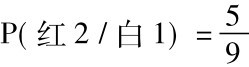
所以根据普遍合取规则,
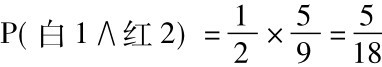
这时产生一个问题: P(红2)是多少? 我们知道P(红2/红1)等于九分之四。我们也知道P(红2/白1)等于九分之五。但我们现在想要知道的是在我们第一次取出一颗之前第二次取出一颗红糖的概率。我们可以获得答案,如果我们认识到第二次取红糖逻辑地等值于:
P(红1∧红2)∨P( ~红1∧红2)
请记取简单陈述q逻辑地等值于复合陈述(p∧q)∨( ~p∧q),所以
P(红2) =P(红1∧红2)∨P( ~红1∧红2)
根据特殊析取规则:
P(红2) =P(红1∧红2) +P( ~红1∧红2)
我们已计算出P(红1∧红2)是 ,我们也计算出
,我们也计算出
所以:
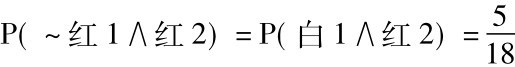
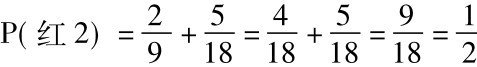
类似的问题都要用条件概率和普遍合取规则去求答案。
3.3 贝叶斯定理
由普遍合取规则得出下面这个贝叶斯定理的简单形式。其步骤如下:
普遍合取规则:
P(p∧q) =P(p) ×P(q/p)
=P(q) ×P(p/q)
用P(p)除两边得
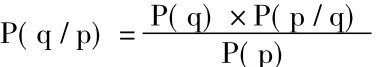
这是贝叶斯定理的简单形式。贝叶斯定理另一形式的证明步骤简化如下:
根据条件概率定义,
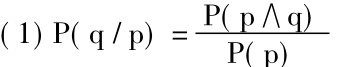
因为P逻辑地等值于(p∧q)∨(p∧~q),得
(2)P(q/p)= P(p∧q) P[(p∧q)∨(p∧~q)]
根据特殊析取规则,
(3)P(q/p)= P(p∧q) P(p∧q) +P(p∧~q)
根据普遍合取规则,
(4)P(q/p)= P(q)×P(p/q) [P(q) ×P(p/q)]+[P( ~q) ×P(p/~q)]
这是贝叶斯定理的另一形式。让我们看看在具体例子中怎样应用这个定理。
假定有两个坛子,坛1内有八个红球和二个黑球,坛2内有二个红球和八个黑球。有人用掷铜钱方法选出一个坛子,然后从所选的那个坛子里拿出一个球。假设坛子里的每个球都有同等的机会被他拿出来,给定他拿出的是一个红球,那么他选择了坛1的概率有多大? 按照贝叶斯定理:

上式代入数值,得出:
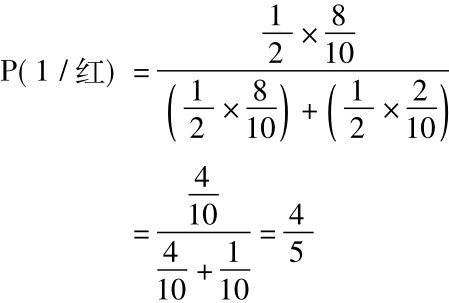
依同样方式计算,得出:
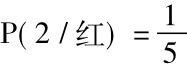
这样,应用贝叶斯定理的结果,确认我们的直觉是对的: 红球由坛1取出比由坛2取出的可能性更大; 它并且告诉我们究竟大多少。
请注意P(q)和P( ~q)的重要性,如果我们不知道选择是随机的,或者不知道用什么方式选择坛子,便计算不出P(1/红)的概率。如果P(1)和P( ~1)是不同的,那么我们的答案就会不同。假设通过投掷一副骰子来选择,如果得“两个1”,就选择坛1,否则选择坛2。按照这种方式,那么
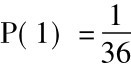
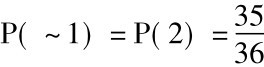
其他照旧,贝叶斯定理得出的概率便是: