描述概率和归纳概率
“概率”一词在我们的语言中至少有两种不同的职能。前面我们集中谈了归纳概率，它的职能是对归纳推理的强度分等级，对前提中含有的事实知识给予结论所作的事实断定的支持程度作出评价。
但有时“概率”一词不是用于评估某一事实主张所获得的支持，而是用于作出一个事实断定。如果你说在二十世纪出生的一个男人活到六十岁的概率是十分之五，你的意思也许简单地是说: 二十世纪出生的男人的百分之五十将活到六十岁。如果这是你的意思，那么你便是作出一个明确的事实断定，你便是描述地使用“概率”这个词。当我们进而评价这个关于事实的断定时，当然归纳概率和主观概率便要参加进来。例如“在二十世纪出生的一个男人将活到六十岁的概率是十分之五”这个陈述的主观概率，根据我们关于现在的成活率、不发达国家的贫穷和超级大国不会放弃核子赌博的知识，可能很低。
一般认为“概率”一词的描述性用法能够由概率演算的频率解释来说明。频率解释是按照属性来表述的以条件概率为基础的一种概率演算解释。在P(A/B)中，属性B叫做基准属性，而具有那个属性的一切个体的集合叫做参照类。例如，在P(活到六十岁/是出生于二十世纪的一个人)中，基准属性是“是出生于二十世纪的一个人”，参照类便是出生于二十世纪的一切人的集合。频率解释把P(A/B)等同于属性A在参照类内的相对频率，就是说:
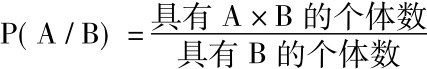
［注意当B是零类时P(A│B)便没有值，因为那时这分数的分母是零。］例如出生于二十世纪的一个人活到六十岁的概率便等于出生于二十世纪的活到六十岁的人数除以出生于二十世纪的人数。
当参照类是有限的，这个定义提供一种简单明了的概率演算解释。但如果参照类是无限大的，有关的分数便没有意义。为了处理(可数的)无限大参照类，我们可以修改相对频率解释。但要做到这一点我们必须首先发展一个无限序列的极限这个概念。试看下面x和o的序列:
xoxoxoxoxox……
小圆点表示这个序列要通过x和o的更替无限地继续下去。能够用生成函数来准确地刻划这个序列: 如果k是奇数，这个序列的第k项是x; 如果k是偶数它便是o。即使这个序列是无限大的，说这个序列的项的半数是x和半数是o，好像是可信的。这就是说，我们要说在这个序列的一切项的类内x的相对频率是二分之一，正像零的相对频率那样。但我们不能够这样说，因为这些相对频率并不是确定的。然而我们能够以下述方式表达我们的直觉判断。这个序列的每一有限的初始段，都有x的一个意义明确的相对频率:
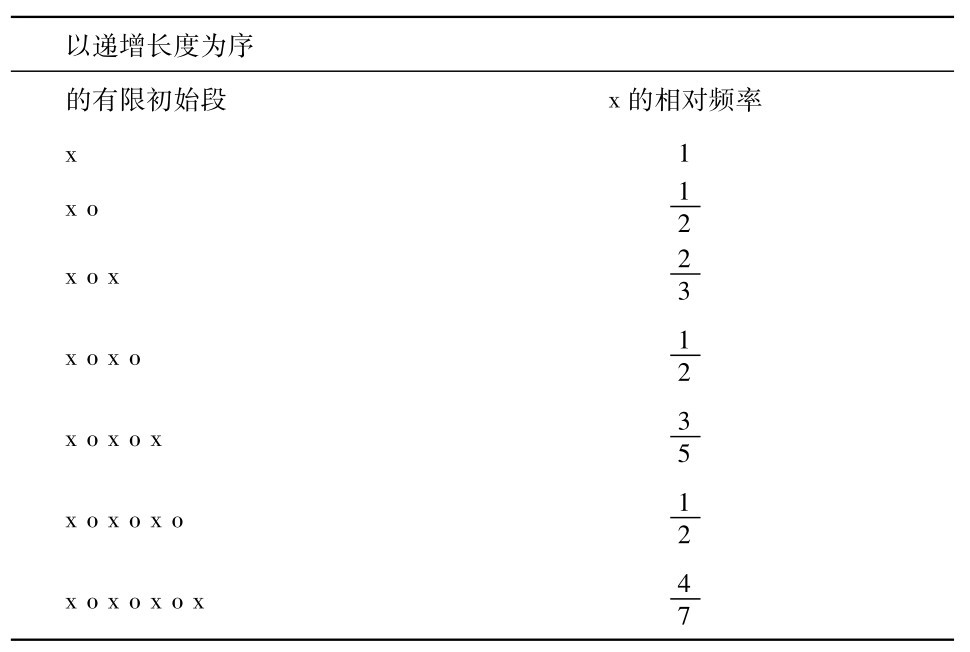
x在有限初始段的相对频率的一览表形成另一个数列:
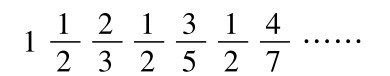
这个数列是由这个函数生成的: 如果k是偶数，序列的第k项等于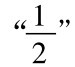
，如果k是奇数，则等于
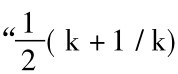”。这个序列有一个很重要的属性。能够证明: 对于所选择的任何有限的误差容限(error tolerance)e，不管e是多么小，这个序列中都有这样的一项，那个项与
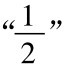的差小于e，并且后继的每一个项和
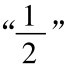的差也小于e。例如，假定e被选定为
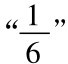，那么序列的第三项
的差是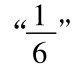
，而且序列中后继的任何一项和
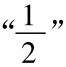的差也小于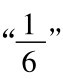
。如果e被选定是
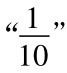，我们便需要寻找序列中的第五项
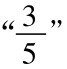。这一项和
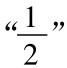的差是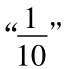
，而后继的每一项和
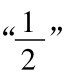的差也小于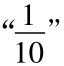
。无论一个多么小的正数被选做e，如果我们在序列中寻找下去，总会找到这样的一项，它和
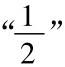的差小于或等于e，而后继的一切项和
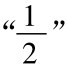的差都小于e。对于序列的这个属性，我们的表达方式是说这个序列的极限是
。
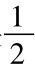我们将把“是一个x”这一属性(在我们原来序列中)的极限相对频率定义为x在有限的初始段内的相对频率序列的极限。因此，x在我们原来的序列中的极限相对频率便是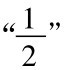
。这就是我们关于原来序列中半数的项是x这个直觉判断的兑现价值。
现在我们可以这样地给P(A/B)的相对频率值下定义: 把具有属性B的个体(参照类的分子)排成一个序列，并且把A在那个序列中的极限相对频率作为概率值。这就提出下式作为概率演算对于无限大参照类的解释:
P(A/B) =A在由那些具有B的个体组成的序列中的极限相对频率。
不幸的是，这个作为概率演算的解释是不行的。其理由如下: 首先，可能有些相干的序列并不趋近于任何极限。因而有些应当下定义的概率便没有任何值。其次，一个序列的极限也许决定于它的各项被排列的次序。就是说，可能当一个无限大参照类B的项被排列成一定序列时便产生A的一个极限相对频率，但当它们被排列成另一个不同的序列时便产生另一个不同的极限相对频率，或者根本不产生任何极限相对频率。这样，所提出的定义也许会使我们得出P (A/B)的两个不同的值，这取决于参照类的分子为形成一个序列而被排列的次序。如果要把概率演算按照属性的观点来展开，它的一个正确解释必须给P(A/B)分配一个并且仅仅一个概率值，除了B是零类的情况以外。
如果发展出着眼于特殊种类的无限序列的概率演算，然后提供一个极限相对频率的解释，这个问题便能够克服。这是一件困难和细致的工作，但已经被完成了。这里不能细谈，赖欣巴赫和冯·米昔斯(Von Mises)对这个问题提出了不同的解决，他们的著作是容易找到的。