抽样和统计推理
2．1 统计假说和概率
假定我们的总体是有二百个学生的集体，这个总体有两个令人关心的属性: 年级和性别。性别的统计分布是简单的，总体的一切分子中间百分之五十是男性和百分之五十是女性。年级变项的分布较有趣: 一年级生一百人，二年级生五十人，三年级生三十人，四年级生二十人。这个分布是四个简单统计假说的合取。
假定我们的总体里有一对孪生兄妹，约翰和珍妮。什么是(随机地)挑选出约翰或者珍妮的概率呢?那是容易算的。选出每个人的概率是二百分之一，所以选出这一个或者那一个的概率便是二百分之二。
这个集体包括二年级生五十人。什么是(随机地)选出一个二年级生的概率呢? 因为每个学生都有相同的机会被选出，并且有五十个二年级生，选出一个二年级生的概率必定是二百分之五十或四分之一。
你现在能够看到在统计假说和概率陈述之间有完全的对应。对于这个总体有一个真的统计假说: 这个集体的四分之一是二年级生。同这个统计假说对应的是这个概率陈述:
(随机地)选出一个二年级生的概率是四分之一。对任何统计假说都是这样。你永远能够表述出相对应的概率陈述。统计假说和概率的这种对应关系是由于使用概率论的一个基本规则才揭示出来的。关于这些规则的知识将加深我们对于样本和总体之间关系的理解，并且将使我们进一步能够理解为什么辩护统计假说和因果假说要使用较大的样本。
2．2 抽样
大多数科学假说所关心的是这么大的总体，以致要检查总体中的每一个人实际上是不可能的。这样，关于总体的任何结论必定是以对总体的仅仅一个样本的研究为根据的。这就是为什么研究抽样这么重要。
大多数科学研究的目的是要知道总体的百分之几显示出某一特定的属性。例如，百分之几的男人患肺癌? 我们关于这个百分比的结论是以由男人的一个总体选出的样本中的肺癌患者的相对频率为根据的。由样本到总体的推理必定是归纳推理，如何辩护这样的归纳推理，是下面几节要谈的问题。这里我们所关心的仅仅是: 由关于总体中的百分比的各个不同的假说能够演绎出关于样本中的频率的什么结论。结果，所能演绎出的一切就是各个不同的可能的样本频率的概率分布。我们这里的目的就是研究和理解这些分布。
2．3 随机抽样和有限制的随机性
一个随机样本是以某种特殊方式选出的样本，这样，并非这个样本本身，而是选择过程具有随机性。在随机抽样中，总体的每个分子都有同等的机会被选出，或者说，都有相同的被选出的概率。对于大的总体，这种无限制的随机性是难以实现的。然而在大多数场合，我们对具体的个人并不关心，却只关心个人的类型，例如妇女或吸烟者。因此，对大多数研究来说，如果抽样对于有限制的一组种类是随机的，也就足够了。这种有限制的随机性就是: 这些种类中的个人被选出的概率必须同他们在总体中的百分比相匹配。
举例来说，假定有人想要测定在特定总体中蓝色眼睛的人的百分比。大家都知道，性别和眼睛颜色之间并不相关。这样只要对妇女进行随机抽样就能够达到我们的目的。虽则选出的概率并不是每个人都一样(男子有零概率)，但选出一个有蓝眼睛的人的概率会恰恰对应于蓝眼睛的人在总体中的真百分比。因而抽样是随机的。这种有限制的随机性是一切研究所必需的。
抽样有退还(replacement)或不退还的区别。差别在于被选出的个人是否有再度被选出的机会。仅当整个样本是总体的显著的小部分，这个区别才是重要的。如果我们对一亿人的总体进行抽样，甚至选出几千人而不退还，对后来的选择机会也几乎没有什么影响，就一切实用目的来说，可以假定是有退还的。以后我们将假设我们的总体同我们的样本比较起来是很大的，或者假设抽样是有退还的。
由总体中选出一个个体叫做一次试验。让我们考虑由我们的二百个学生的总体中抽样(有退还)。让我们把所有的人归入两类: 新生(F)和其他的(R)。在连续的三次试验中共有几种不同的互相排斥的可能结果的排列，如下:
(F，F，F) (F，F，R) (F，R，F)
(R，F，F) (F，R，R) (R，F，R)
(R，R，F) (R，R，R)
以上每一个序列都代表个别结果的合取。例如，第一个代表第一次试验选出一个新生并且第二次试验选出一个新生并且第三次试验选出一个新生。
抽样应是随机的这个要求保证在任何试验中选出一个新生和任何其他试验中选出一个新生并不相关，因此我们能够使用乘法规则来计算一个三次试验序列的各种可能结果的概率:
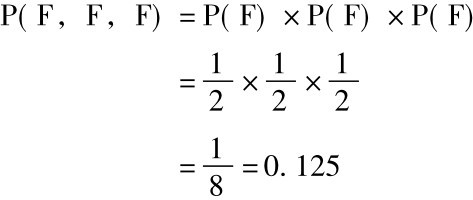
因为P(F)=P(R)=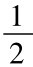
，其他七个序列都恰恰有相同的概率。
就三次试验来说，F的数目可以有四个不同的值: 0，1，2，3。就是说，结果可以没有F，一个F，两个F或者三个F。让我们用Y来代表有这四个值的变项。我们刚才已经算出P(F，F，F) =0．125。没有F的概率［即P(R，R，R)］也是一样。选出F或者“F，F”的概率可用加法规则来测定。三个互相排斥的序列(F，R，R)、(R，F， R)和(R，R，F)是只有一个F的。得出这三个序列的任一个的概率，按照加法规则是三个概率的总和，即八分之三(或零点三七五) 。得出两个F的概率也是八分之三。这样，三次试验的概率分布P(Y)，如附图2所示。
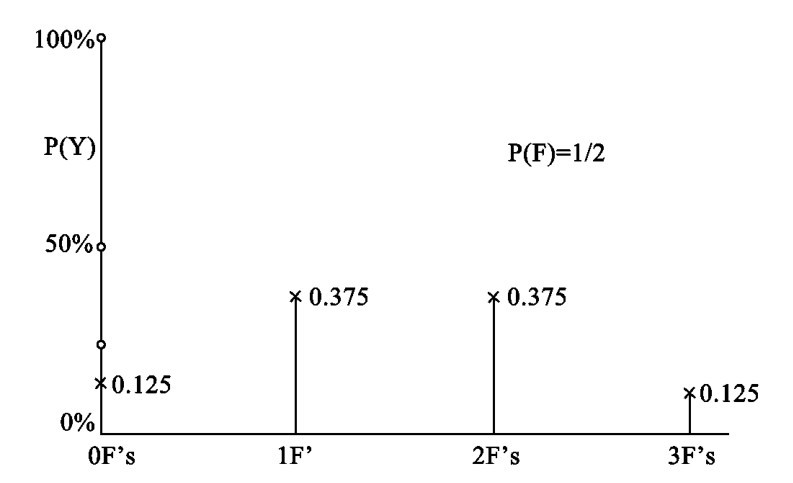
图2 在三次随机试验中F的数的概率分布
要算出四次或五次试验的P(Y)的分布，需要分别考查十六个和三十二个不同的序列，但一般方法同三次试验一样，使用乘法规则来计算个别序列的概率，然后使用加法规则来计算F的各个不同的可能的数的概率。
2．4 大样本
我们给几次试验所算出的分布是根据样本中新生的数来作出的。例如，我们发现在三次试验中选出两个新生的概率是零点三七五。但是，一般地说，根据相对的数或者相对频率来思考，比起根据一个实际的数更有用得多。这是因为我们需要比较两个或更多的样本，而这些样本可以大小不同，所以相对频率提供较好的比较方法。
对于较多次试验的抽样分布，变项Y将不代表新生的可能的数，而代表新生的可能的相对频率——就是用样本的总人数来除新生的数。例如，我们所记录的不是在十个人的样本中选出五个新生的概率，而是得出相对频率零点五，即十分之五的概率。如果你要弄清楚有一个较大的样本(例如五十人)对于概率分布的影响，你所寻找的不是从五十人中得出五个新生的概率，而是得出相对频率0．5的概率，即从五十人中得出二十五个新生的概率。这会帮助你弄明白有一个五十人的而不是十人的样本意义何在了。
所有这些抽样分布的一个显著特点就是: 最概然的样本频率是和总体中的比率一致的。在我们的例子中，新生在总体中的比率是零点五，而有最大概率的样本频率总是零点五(或者尽可能地靠近零点五)。在这个总体的四个人的样本中新生的最概然的数是二，相对频率是零点五，在一个二百五十人的样本中，新生的最概然的数是一百二十五，相对频率又是零点五。
零点五不仅是最概然的频率，而且在一种清楚地可定义的意义上，它也是平均频率或期望频率。这个期望频率的概念对于小样本是最显而易见的，但也适用于不管多么大的样本。
例如，试考虑仅仅两个人的样本。现在，试设想在四个不同的场合［(F，F)，(F，R)，(R，F)，(R，R)］中选出集体里的两个学生。因为两次试验都选不出新生的概率是四分之一，你可以期望在四个场合的一个中得不到新生。同样地，因为在两次试验中得出一个新生的概率是二分之一，你能够期望在两个场合中得出一个新生。最后，因为在两次试验中得到两个新生的概率又是四分之一，你能够期望仅仅在一个场合得出两个新生。这样，在所有四个场合中你能够期望的是总共四个新生［(1×0) +(2×1) +(1×2) =4］，那相当于四分之四的平均值，或者每个场合一个新生。所以，平均说来，两个人的样本可得出一个新生，这就是相对频率零点五。
那么，在随机抽样中，最概然的相对频率和期望的相对频率两者都对应于被抽样的总体中的比率。这对于一切大小的样本都是有效的。在概率论和数理统计教材中，期望频率常常被叫做频率的平均值(meanvalue of the frequency)。
在两个人的样本中，得出一半新生的概率是百分之五十，十个人的样本中概率是百分之二十五，一百人的样本中概率是百分之八，而二百五十人的样本中，概率只有百分之五。这样，样本越大，你实际上达到期望频率的概率便越小。看来好像奇怪，其实是有道理的。
如果你仅仅作三次或四次试验，你有很好的机会将得出半数新生(事实上四次试验中的概率是0．375)。但如果你作一百次试验，你不会真的期望恰恰得到五十个新生。但是，你期望所得到的相当靠近五十个新生。就概率分布来说，期望值的“靠近”是根据平均偏差(deviation from the mean)来下定义的。
平均偏差基本上是相对频率的差别问题。例如，相对频率零点四和平均值零点五相差零点一。然而，对一个分布的平均偏差通常是经由概率来间接地下定义的。偏差的标准测度单位被称为标准差(standarddeviation)。什么是标准差呢?
让我们从一个特定分布开始。试考虑由其半数分子显示出所关心属性的一个总体作一百次试验中相对频率的抽样分布。平均(或期望)数是五十(或样本频率零点五)，由一百次恰恰得出五十的概率是零点八。但是，得出的数在四十六和五十四之间的概率是三分之二，或百分之六十七。从零点四六到零点五四的一切样本频率都被说是在平均值的一个标准差之内。
同样地，从零点四到零点六的一切样本频率的概率的总和大约是百分之九十五。这个范围内的所有频率被说是在平均值的两个标准差以内。暂且不管为什么百分之九十五是两个标准差，重要的是要记取两个标准差之内的一切可能的频率的总和概率是百分之九十五。而且两个标准差在科学推理中起特殊的作用，因为对一个好的归纳推理来说，百分之九十五一般被认为是足够高的概率。
在三个标准差和百分之九十九的概率之间存在着同样的关系。在平均值的三个标准差以内的一切频率的总和概率约计百分之九十九。这些关系在附图3中显示出来。
根据概率来给偏差下定义的理由，是使所得到的测度对试验的次数保持独立。不管样本的大小，“两个标准差”(简写为2SDs)对于任何的抽样分布都具有相同的意义。它所指称的是其总和概率为百分之九十五的，在平均值周围的一切可能的样本频率。
即使只做几次测验，你也开始明白为什么较大的样本是可取的了。有了较大的样本，观察到F的相对的数“靠近”F在总体中的比率(百分之五十)，便有较高的概率。换句话说，样本大了，所选出F的相对数不靠近半数的概率便降低了。显然，无一个F或者全是F是离F占半数最远的。只试验两次便有百分之五十的概率选出或者无F或者全F(用加法规则)。试验三次，选出无F或全F的概率便降低到百分之二十五。试验四次它便降低到约百分之十二，五次便降至约百分之六。反过来，随着样本由二次增至五次，达到靠近F占半数的概率，便由百分之五十增至约百分之九十四。试验的次数越多，这个趋势就越明显。
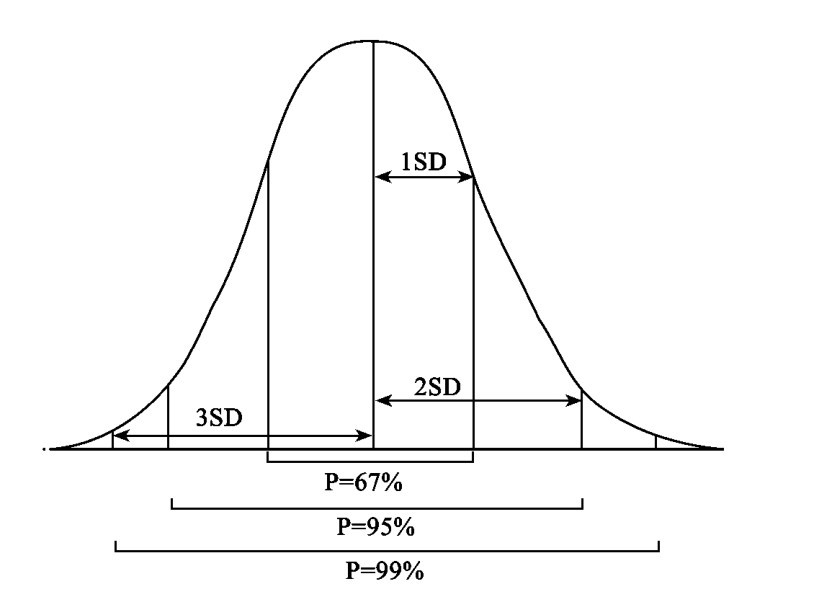
图3 标准差
如果你挑出一个固定的高概率，比如百分之九十五，那么，样本越大，有那样的高概率的可能的样本频率集合(这是在两个标准差以内的所有样本频率)离平均值就越近。就是说，这个集合中的频率越来越靠近期望频率。也可以倒转过来看看: 把频率的变动范围固定起来，让概率发生变化。例如，让我们说在区间零点四到零点六之间的任何频率是“靠近”零点五的。那么对十次试验的样本来说，样本频率“靠近”零点五的概率只是百分之六十五［按照加法规则，P(0．4， 0．5或0．6) =P(0．4) +P(0．5) +P(0．6) =0．65］，但对一百次试验的样本来说，样本频率同样地“靠近”零点五的概率便是百分之九十五。这样，样本越大，样本频率将“靠近”期望频率的概率便越高。
为什么科学家一般偏爱大样本，这就很清楚了。一个随机样本中任何属性的期望频率和那个属性在总体中的比率是相同的。这样，样本越大，样本中所观察到的频率便以越高的概率“接近于”总体中的实际比率。所以，一般地，较大的样本是总体中实际比率的较好的指示器。
本节所用的例子涉及有相等概率的抽样，就是说，任何一次选择的两个可能结果，新生或其他，都有百分之五十的概率。这种情况最容易掌握，至于有不相等概率的抽样，在基本原则上并没有差别。例如，由我们二百个学生的总体中选出二年级生的概率只是百分之二十五，选出其他的概率是百分之七十五。这是不相等的概率。二年级生的相对频率的概率分布便和新生的有所不同。主要差别在于平均值是零点二五而不是零点五，因而在分布表上显得有点不对称。但像以前一样，样本越大，样本频率接近于总体比率(现在是零点二五)的概率便越高。