简单枚举法
我们都知道糖溶解于水中。不仅关于某一块糖,而且所有的糖我们都知道是这样。我们的知识是从哪里得来的呢? 我们有一次发现一块糖在水里溶解了,我们还发现其他许多糖块也是如此,别人还发现其他成千上万的糖块都是这样。另一方面,没有人发现过糖不溶解于水(纯粹的、未包含很多糖分的水)中的例子。这个大量的相同的事实引导我们作出普遍的结论: 每一块糖都可溶解于水中。
这是称为简单枚举法的那一种归纳推理的例子。
定义10: 简单枚举法是任何这样的推理: 以接受某一普遍规律性的个别实例的成对陈述为根据,把那个普遍规律性陈述作为结论加以接受。
普遍规律性的陈述可以有各种不同的形式,其中之一就是全称肯定陈述:
(A)“每一个S都是P”
或是全称否定陈述:
(E)“没有一个S是P”
上面两种方式所陈述的规律性可以同样地陈述如下:
(1)“对一切x成立: 如果f(x),那么g(x)”,这里f(x)和g(x)是有一个变项的语句形式。例如: “对一切x成立: 如果x在汽油中下沉,那么x在水中下沉”,这在日常语句里就会是“如果某一东西在汽油中下沉,那么它也在水中下沉”。
但有的普遍规律性,不能够用(1)型的陈述来表示,因而也不能用(A)型和(E)型的直言陈述来表示。例如下面这个陈述所表示的规律性:
对一切x和y成立: 如果x>y,那么y<x。
便不能够用(1)型的任何陈述来表示。因为在那一类型中,每一语句形式都只含有一个变项。而在上述陈述所表示的规律性中就需要使用两个变项x和y,因而在(1)之外,还有下面这种形式:
(2)“对一切x和y成立: 如果f(x,y),那么g(x,y)”,这里f(x,y)和g(x,y)都是含有两个变量的语句形式。(2)也必须被看作是普遍规律性陈述所采取的形式之一。
依此类推,还有其中每一语句形式含有三个变项的规律性陈述,就更不能够用(1)型或(2)型来表示了,所有这些形式都归入以下的普遍公式:
(n)“对一切x1,x2,……,xn成立: 如果f(x1,x2,……,xn),那么g(x1,x2,……,xn)”。
自然科学中所遇见的许多普遍规律性,都不能用简单的直言肯定或否定陈述来表示,因而不能够用(1)型的陈述而要用含有较多变项的陈述来表示。那些关于若干不同量值之间的函数关系的规律性尤其是这样。
例如自由落体定律在物理学教科书中往往用以下公式来表示:
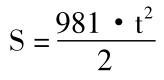
但必须说明S和t代表什么,这个方程式才能反映有关定律。完整的表述应是:
对一切s和t成立: 如果s代表一个自由落体在时间t(以秒计算)内所落下的距离(以厘米计算),那么s=(981·t2)/2。
显而易见,这个陈述属于(2)型:
对一切x和y成立: 如果f(x,y),那么g(x,y)。
根据以上说明,简单枚举法定义中所用“普遍规律性陈述”一词包括下述形式的一切陈述:
对一切x1,x2,……,xn成立: 如果f(x1,x2,……,xn),那么g(x1,x2,……,xn)。这样,在简单枚举法中,结论不必具有“每一个S都是P”的形式,这仅仅是它的许多可能的形式之一。
现在我们要说明枚举法定义中的“成对陈述”一词的意义。如果普遍规律性陈述具有如下形式: “对一切x1,x2,……,xn成立: 如果f(x1,x2,……,xn),那么g(x1,x2,……,xn)”,那么,这种规律性的个别事例的成对陈述就是下面这种一对对的陈述: “f(a1, a2,……,an),g(a1,a2,……,an)。”这里“a1,a2,……,an”是分别代表变项“x1,x2,……,xn”的一定值的常项。例如,“一切糖都溶解于水中”这个陈述和“对一切x成立: 如果x是糖,那么x溶解于水中”这个陈述是对同一个规律性的描述。这种规律性的一个特殊事例由下面这一对陈述所描述: “这是糖”和“这溶解于水中”。另一个例子是自由落体的距离与时间之间的函数关系,这个关系可这样表述: “对一切S和t成立: 如果S代表一个自由落体在时间t内(以秒计)所落下的距离(以厘米计),那么S=(981·t2) /2”。这种规律性的一个特殊事例由下面这一对陈述来表述: “490.5厘米是一个自由落体在一秒钟内下落的距离”并且“490.5=(981·t2) /2”。
现在可以写出枚举归纳法的一般推理形式如下:
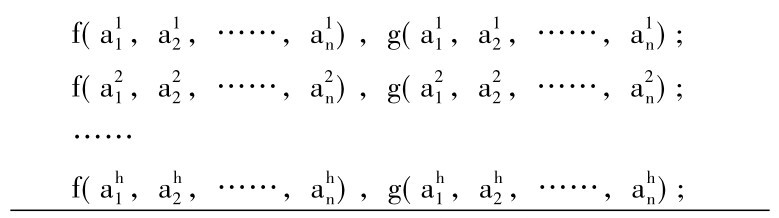
所以对一切x1,x2,……,xn成立: 如果f(x1,x2,……,xn),那么g(x1,x2,……,xn)。在n=1这个最简单的场合,这个一般形式便简化为:
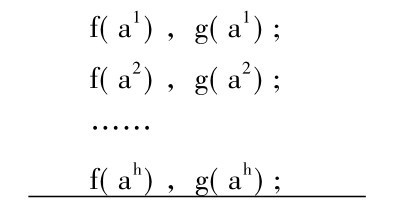
所以对一切x成立: 如果f(x),那么g(x)。
例如:
a1是糖,a1溶解于水中;
a2是糖,a2溶解于水中;
……
ah是糖,ah溶解于水中;
所以,对一切x成立: 如果x是糖,那么x溶解于水中,就是说,一切糖都溶解于水中。
从上面可以看到: 在枚举归纳法的推理中,结论所陈述的是普遍规律性,前提所陈述的是普遍规律性的个别事例。前提是用成对陈述来表述的,每对陈述中有一个陈述规定了作为结论的条件陈述的前件,另一个陈述规定了它的后件。例如: “a1是糖”,这个前提是结论“如果x是糖,那么x溶解于水中”这个条件陈述的前件的规定,而“a1溶解于水中”则是它的后件的规定。
让我们把规定条件陈述前件的前提叫做“归类的前提”,把规定其后件的前提叫做“描述的前提”。
很容易看出: 枚举归纳法的前提和结论之间存在着下述关系:(1)结论并不由前提逻辑地得出,但(2)描述性前提由结论和归类性前提逻辑地得出。事实上,如果各个不同对象a1,a2,……,an是糖,并且这些对象溶解于水中,那么并不得出一切糖都溶解于水,即并不能得出: “对一切x成立: 如果x是糖,那么x溶解于水中。”但如果有“对一切x成立: 如果x是糖,那么x溶解于水中”(结论),而且“a1是糖”(归类性前提),那么就逻辑地得出: “a1溶解于水中”(描述性前提)。
这样,枚举归纳法不是演绎推理,枚举归纳法的推理形式也不是可靠的,所以这种推理可以从真前提作出假结论。因而枚举归纳法不能够作为主观充分置信的推理而被认为是正确的。但如果满足了一定条件,它最多可以作为主观上不充分置信的推理而具有较高的归纳强度。
作为主观上不充分置信的推理,让我们讨论一下枚举归纳法的归纳强度的条件。上面已经指出,枚举归纳法的强度也就是我们接受其结论所持有的置信度,不超过那个结论相对于前提和推理者所掌握的知识总汇而具有的概率。在下述枚举归纳法中:

左边的前提是归类性前提,右边的是描述性前提。为简便起见,任何枚举归纳推理中的h个归类性前提的合取将以Lk表示,而k个描述性前提的合取将以Qk来表示。并且一个归纳推理的结论将以H表示,而据之以检查某一归纳推理结论的强度的推理者知识的总汇将用k表示。使用这些缩略符号,我们就可以这样地表示枚举归纳法:
Lk∧Qk
所以 H
结论H相对于前提Lk和Qk以及知识总汇K的概率以下述公式表示:
(1)P(H/Lk∧Qk∧K)
把我们据以计算H的概率的那些陈述重新排列一番,(1)可改写为:
(2)Pk(H/Qk∧Lk)
根据贝叶斯定理:
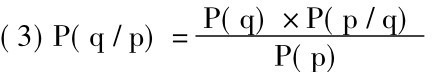
现在我们把K和Lk都作为推理者已经掌握的背景知识,用B表示,加入定理中,并且以
H代入q
Qk代入P
我们就得到下述求得这个归纳结论的概率的公式:
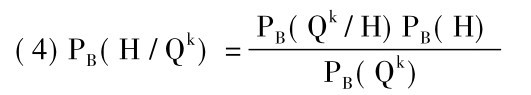
但已经指出,在枚举归纳法中,描述性前提由结论和归类性前提逻辑地得出,用符号表示:
(5)H∧Lk→Qk
例如,如果我们考察下述推理形式:

可立即看出在这里由结论
每一s都是p
和归类性前提
a1是s,a2是s,……,an是s
得出描述性前提(https://www.daowen.com)
a1是p,a2是p,……,an是p。
但既然
H∧Lk→Qk
因此
(6)H∧(Lk∧K)→Qk
也就是
H∧B→Qk
但
(7)PB(Qk/H)=1。
因为推断相对于理由的概率等于1。
那么公式(4)就可以简化为
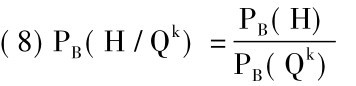
把这个公式和上一节我们讨论假说推理时得到的公式(4)比较一下,它的形式是
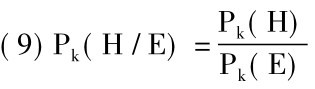
我们注意到两者的相似。公式(8)恰恰是公式(9)的特殊情况,用表示描述性前提的Qk代入证据或前提E的一般符号而得到的。这一点也不奇怪,因为假设归类性前提包括在推理者的知识总汇K(现在用B来表示)中,枚举归纳法便仅仅是假说推理的一种变形。
假说推理的特征是: 它的结论H并不由前提E和知识总汇K得出。以符号表示:
(10)E∧ →—K \ H,
但前提E却由结论H和知识总汇K逻辑地得出。以符号表示:
(11)H∧ →—K E
另一方面,在枚举归纳法中,我们有以下的关系: 结论H并不由前提Lk和Qk以及知识总汇K得出。用符号表示:
(12)Lk∧Qk∧ →—K \ H;
但描述性前提Qk由结论H和归类性前提Lk逻辑地得出。以符号表示:
(13)H∧Lk—→Qk
但要是假设归类性前提包括在知识总汇K中,即Lk∧K=K,并且如果用E来表示归类性前提和描述性前提的合取,那么在枚举归纳法中有效的关系(12)和(13)使我们得出以下关系,这些关系是假说推理的特征:
(14)E∧K—\→H
(15)H∧ →—K E
公式(14)是简单地用符号E替代符号Lk和Qk的合取、由公式(12)得到的。公式(15)是由公式(13)这样地引出的: 如果Lk包括在K中,那么凡是由H∧Lk得出的,也就由H∧K得出,因而如果
H∧Lk—→Qk
那么
H∧K—→Qk。
另一方面,如果Lk包括在K中,那么
H∧ →—K Lk
因而
H∧K—→Qk·Lk
即是
H∧K—→E
公式(14)和(15)也可以这样来解释: 结论并不由前提和知识总汇得出,但前提却由结论和知识总汇得出。这就表明,如果归类性前提Lk包括在知识总汇K中,那么枚举归纳法就是假说推理的一种变形。
既然如此,上节关于假说推理的归纳强度的条件所说的也适用于枚举归纳法。
主观地不充分置信的推理要成为合理的,便必须满足下面这个一般条件: 对于由充分置信的并且正确地接受的前提引出的结论所持的置信度d不得超过那个结论相对于前提和知识总汇的概率,也就是说,对结论H所持的主观概率不得超过这个推理的归纳概率。如果枚举归纳法的归类性前提Lk包括在推理者的知识总汇中,那么,这个条件就简约为要求对结论的置信度d满足下列不等式:
d≤Pk(H/Qk)
在讨论假说推理的合理性条件时,我们提出了几个定理。现在就它们与枚举归纳法的关系进行分析。
(1)如果假说推理的结论H相对于推理者知识总汇的概率,即H的先验概率,等于0; 即如果K排除了那个结论的真理性,那么这个推理相对于那知识总汇就不是合理的。同一定理适用于枚举归纳法,这里如果初始的知识总汇蕴涵着结论H的否定,那么那个结论就不能够合理地被接受。
在枚举归纳法中,结论总是这样一个全称陈述: 指出任何满足条件f的东西也满足条件g。如果推理者的初始知识包括有关于一个满足条件f而不满足条件g的对象的知识,即如果预先知道有一个对象不满足结论中所表述的规律性,或者至少知道这样一个对象是存在的,即使不能够明确指出是哪一个,这种初始知识就蕴涵了那个结论的否定。
符合一个给定规律性的成千上万个正面事例都不足以使我们接受这个规律性,只要已知道单单一个违反它的实例。
(2)(a)一个假说推理结论的先验概率,即它相对于初始知识K的概率越高,并且/或者(b)前提相对于知识总汇K的先验概率越低,那个结论的概率(条件概率)就越高,因而那个结论可被接受的置信度越大。
这个定理当然也适用于枚举归纳法,并且它可以由下述公式得出。这个公式给出一个归纳结论本身相对于包括归类性前提Lk在内的背景知识总汇K的概率。
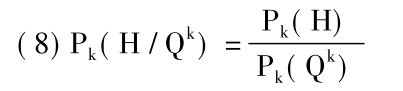
根据公式(8),上述定理就是分子越大并且/或者分母越小,分数便越大这一事实的一个简单推断。
关于(a)的补充。由于枚举归纳法结论是一个全称陈述,例如“每一S都是p”这个类型的陈述; 可以说结论的普遍性越小,它的先验概率Pk(H)便越高。这是因为一个普遍性较小的结论总是由普遍性较大的得出,而不是相反。而概率演算证明如果B(相对于知识总汇K)由A得出,而A(相对于K)并不由B得出,那么B相对于K的概率(推断的概率)高于A的概率(理由的概率)。
因为归纳结论的普遍性越小,它的先验概率就越高,因此,在给定描述性前提和给定初始知识总汇的条件下,一个结论的普遍性越小,那个结论可被接受的置信度就越大。
一个给定的对象集a1,a2,……,an,在描述性前提中被断言为P,可以被归类性前提以各种不同方式来分类。例如,对于后来被我们断定为溶解于水的许多不同的糖块,可以被归类为糖,也可以被归类为蔗糖。这样,随着我们实验的结果,我们不仅能够作出一切糖都溶解于水的普遍结论,也能够作出一个普遍性较小的结论,即一切蔗糖都溶解于水。后一结论得到前提更好的支持,就是说,我们能够以较大的置信度去接受它。
如果我们的描述性前提对K个对象a1,a2,……,ak断言它们是p,那么根据这些前提作出的一切可能的归纳结论中普遍性最小的便是“每一S0都是p”,S0在这里是其外延仅仅包括对象a1,a2,……,ak的一个名词。这个结论也是充分置信的,因为在这个例子中归纳是完全的。例如,在关于糖的例子中,发现一定数量的糖块都溶解于水中以后,我们能够得出充分置信的归纳结论说至今检验过的每一块糖都溶解于水。在这个例子中我们的推理仅仅是实际经验的简单记录。
但在进行归纳推理时,我们不仅有兴趣于使得到的结论有尽可能高的概率,我们还对它可能提供的知识也很感兴趣,希望由它可以导出有关某一类的一切对象的某些知识。例如在我们研究动物界时,我们对于有关一切的鼠,一切的狗,一切啮齿动物,一切哺乳动物的知识感兴趣。换句话说,我们愿意通过归纳法得到普遍的结论,该结论将以动物学所用的专门术语中的一个名词作为它的主词。
一般情况是我们所选用的专门术语并不包括上述结论中的名词S0,因为S0的外延就是并且仅仅是那些已检验过的对象a1,a2,……,ak的集合。因此我们不能够用那些术语来表达可由给定前提引出的普遍性最小因而概率最高的归纳结论。所以我们必须满足于一切能够用有关术语来表达的结论中普遍性最小因而概率最高的结论,而非所有那些一般地可由给定前提用归纳法推出的结论中普遍性最小因而概率最高的结论。
具有“每一S是P”形式的任何陈述,都能够作为归纳法结论由陈述a1,a2,……,ak都是P的前提推出来,只要这些对象是在那个陈述的主词S的外延中。在给定术语中,一个具有“每一S都是P”形式的结论是可由断言a1,a2,……,ak都是P的前提推出的那些结论中普遍性最小的,如果为此目的所选用的术语并不包含任何这样地从属于S之下以至其外延包括一切对象a1,a2,……,ak的名词。因此,在所选用术语中,结论“每一S都是P”是由断言a1,a2,……,ak都是P的前提中推出的普遍性最小的归纳结论,如果那些对象除去它们都是S这一点以外,并不呈现出任何其他可用有关术语表达的更密切的相似性。要是这些对象呈现出更密切的相似性,即是如果它们归入那从属于S之下的名词S'(在所选用专门术语范围内的),那么结论“每一S都是P”便不是可由给定前提推出的那些结论中普遍性最小的因而概率最高的结论。在这样的情况下,“每一S'都是P”将是可由给定前提推出的那些结论中普遍性较小的。
例如要是一千只受检验的老鼠都有属性P(比方说它们都作出某一特定的药物反应),那么就可能用归纳法由这个事实(并且用系统动物学所用的术语)推出普遍性程度不同的许多结论。可以作出一切老鼠都有属性P的结论,或者一切啮齿动物都有属性P的结论,或者一切哺乳动物都有属性P的结论,等等。根据这些关于一千只老鼠有属性P的前提,“一切哺乳动物都有属性P”这个结论较之“一切啮齿动物都有属性P”的结论概率较低,较之“一切老鼠都有属性P”的结论就更低了。但对“一切哺乳动物都有属性P”的结论,如果所根据的是对另外一千头动物的检验,这些动物并不都具有老鼠所共有的那些特征,即检验一千头并不都是老鼠,也不全是啮齿动物,却包括例如老鼠、狗、猫、牛、马等等在内的动物,它的概率就会提高。
从上例可以看出,由同一数量的前提推出的归纳结论“每一S都是P”,如果前提所提及的对象较多变化,即是说,如果它们除了都是S之外呈现出的相似性越少,概率就会越高。前提中所提及对象呈现出来的那些密切相似性越少,在由这些前提可用归纳法推出的所有那些结论当中,我们的结论的普遍性就变得越小。而由于成为普遍性较小的结论,它因而成为概率较高的结论。
总括起来,前提所提及的对象越多变化,就是说,比一个给定结论普遍性较小的、能由那些前提推出的结论越少,作为归纳结论由若干前提推出的那个普遍定理的概率就越高。
所有关于一个归纳结论的概率所说的都是指它的先验概率,即它相对于知识总汇K的概率。这个知识总汇并不包括描述性前提在内。然而正如我们已经指出的,结论的后验概率相对于初始知识总汇加上描述性前提的概率,是简单地同它的先验概率成比例的。因而可以说,前提所提及的对象越多变化,它们除了都属于结论主词所指对象这一点以外所呈现的相似性越少,结论的后验概率就越高。
关于(b)的补充: 一个归纳结论相对于它的前提和知识总汇k (包括归类性前提在内)的概率的公式如下:
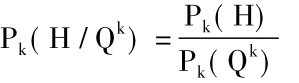
这公式表明,对给定的大于零的先验概率Pk(H)来说,Pk(Qk)越低,即描述性前提的合取Qk(例如: “a1是P,a2是P,……,ak是P”)相对于K的概率越低,结论的后验概率Pk(H/Qk)就越高。以相似于假说推理的方式来推论,我们很容易证明: 随着新的描述性前提的增加,它们的合取的概率通常会变小。假定给k个描述性前提的合取Qk添加一个新的描述性前提q; 这就得出k+1个描述性前提的合取,用Qk+1来表示。合取的概率的公式便是:
Pk(Qk+1)
=Pk(Qk∧q)
=Pk(Qk)×Pk(q/Qk),
这就证明,只要Pk(q/Qk)<1,那么
Pk(Qk+1) <Pk(Qk)
这表示在添加任何一个本质上新的(并不相对于给定知识总汇由已有前提得出的)描述性前提时,这些前提的合取的概率就要降低。因为一个归纳结论的后验概率同它的描述性前提的概率成反比,因而这个结论所根据的(互相独立的)前提的数量越大,这个归纳结论的后验概率就越高。
现在把对归纳结论的概率的分析作一个总结:
(1)一个归纳结论相对于前提Qk和知识总汇K的后验概率等于0,如果它的单独相对于K的先验概率等于0的话,在这种情况下归纳推理是没有结论的。
(2)(在特定场合一切可能结论中的)一个结论的普遍性越小,它的先验概率就越高; 而它的先验概率越高,它的后验概率也就越高。这个条件也可以这样来表述: 给定一个由断言对象a1,a2,……,ak都是P的前提推出的具有“每一个S都是P”形式的归纳结论,那些对象除都是S外所共同的属性越少,就是说这些对象越是多样的,这个结论的后验概率就越高。
(3)(互相独立的)前提的数量越多,这个结论的后验概率越高。
如果推理者根据他所正确地接受的前提达到以不超过那个结论的后验概率的置信度来接受结论的话,推理相对于知识总汇来说就是合理的。上述定理规定了一个结论的后验概率所依赖的条件。因此,上述定理也就规定了(根据正确接受了的前提)结论可被接受的置信度所依赖的那些条件。
可以看出,一个要谨慎地进行归纳推理并使他的错误风险为极小的推理者必须作出普遍性程度小的结论,但一个结论的普遍性程度越小,能够根据它作出的预测就越少。反过来,我们能够通过结论借以被确认的那些事例的增加,伴随着采取适当措施研究尽可能多样的事例,来减少同结论的较大普遍性相联的风险。这样,把影响结论概率的两个因素适当地配合,就会得到符合应用需要的足够普遍的结论,而不冒超过可接受的水准的错误风险。
