亨佩尔悖论
如果说，古德曼悖论所强调的是通常的枚举归纳推理将要导致互相矛盾的结论，亨佩尔悖论所突出的则是这些推理将导致违反直觉的推断。亨佩尔悖论的提出比古德曼悖论要早几年。对亨佩尔悖论的讨论比对古德曼悖论的讨论还要更热烈，文献更多，意见更不一致。本节对此只能作较简单的介绍和分析。
2．1 亨佩尔对确认悖论的看法
亨佩尔悖论又称乌鸦悖论(paradoxes of the ravens)或确认悖论(paradoxes of confirmation)。他在1945年的《确认逻辑研究》中展开这些悖论。要理解亨佩尔的研究，我们首先要弄清楚他的目的何在。他的目的是要决定假说h的概率在获得新证据e(相对于我们为简单起见可看作概率等于1的先前证据)时，是否有增加和增加多少。这样他要讨论的问题便是: “给予这两个非定量的关系概念: 确认和不确认(disconfirmation)以准确的定义，就是说，要给‘E确认H’和‘E不确认H’这两个短语的意义下定义。(如果E对H既非确认亦非不确认，我们就说E对于H是中立的或不相干的。)”[8]但实际上亨佩尔所做的是给“E是H的正面事例”下定义，并且假定正面事例永远是确认性的。(就是说，如果E是H的正面事例，那么H给定E会比H给定重言式证据，概率更高。)但这个假定是不正确的。关于什么时候正面事例才是确认性的，我们下面再谈。
亨佩尔首先批评两种标准看法，以便为提出他自己关于“确认实例”的理论作准备。这两种看法就是尼柯标准和预测标准。首先关于尼柯标准。尼柯问道，一个特殊命题或一个事实如何能够影响一个定律或全称命题的概率呢? 假定我们要检验的定律是“A必然伴有B”，如果这个事实是在A出现时也有B，它就对这个定律有利; 反之，如果是在A出现时没有B，它就不利于这个定律。尼柯假定只有这两种使一个事实能够直接影响一个定律的概率的方式。他称这样的两种基本关系为确认和否认(invalidation)。亨佩尔首先把尼柯的定律用符号逻辑记号表示为(x)(P(x)⊃Q(x))，就是用形式蕴涵来翻译尼柯的“必然伴有”。由于后一个概念会有因果必然性的意义，便有人提出异议，应把它翻译为P(F(x)⊃G(x))或者也许F →—□ G，这里“ →—□ ”是必然伴有的记号。下面我们试把亨佩尔的全称假说都读作这个意思，看看这对他的论证有什么影响。
亨佩尔在下述两点上批评尼柯标准: 第一，它并不适合于全部的确认理论，因为它并不给存在假说或含有混合量词的假说的确认提供标准。亨佩尔这样说的意思也许是: 当一个全称假说被否认时，它的由此而确立的否定陈述∃(x)(F(x)∧～G(x))并不是作为一个定律来确立的。按照模态逻辑的原则，
(x)(F(x)⊃G(x))的否定并不是
(∃(x) (F(x)∧～G(x))，而是
(x)(F(x)∧～G(x))。这样，亨佩尔的第一点是对的。但亨佩尔进一步认为尼柯标准甚至对全称条件陈述也不适合。
他的反对理由基于一个陈述的形式和内容之间的区别。逻辑上等值的陈述被认为内容相同，但可以有不同的形式。亨佩尔主张我们想要确认或否认的假说是这个全称概括的内容。这样逻辑上等值的全称概括被认为是相同假说的不同表述。但尼柯标准是根据一个假说的表述形式来作出的，如果它对同一假说的不同表述得出不同的结果，那么，把它看作一个假说的确认和否认实例的判据，它是不一贯的。亨佩尔证明它事实上就是这样。试看一个全称条件陈述: (A): (x) (F(x)⊃G(x))。按照尼柯标准，具有F(a)∧G(a)形式的一个实例会确认这个假说; 具有F(a)∧～G(a)形式的实例便会否认它。而具有～F(a)∧G(a)和～F(a)∧～G(a)形式的实例则是对它不相干的。但同一假说能够以不同形式表达为(B): (x)( ～G(x)⊃～F(x))，在这个情况下，尼柯标准说～F(a)∧G(a)是确认性的; 或者表达为
(C): (x)［(F(x)∨～F(x))⊃( ～F(x)∨G(x))］
在这个情况下，那两个“不相干的”实例就都是确认性的了; 或者表达为
(D): (x)［(F(x)∧～G(x))⊃(F(x)∧～F(x))］
在这个场合下，按照尼柯标准，确认实例便是逻辑上不可能的! 因此，需要放弃尼柯标准。
对于这个批评我们可以像下面这样答复: 虽然(x)(F(x)⊃G(x))逻辑地等值于(x)(～G(x)⊃～F(x))和其他两式，
(x) (F(x)⊃G(x))却不等值于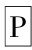
(x)(～G(x)⊃～F(x))。而我们所感兴趣的却是对物理定律的确认。因此，亨佩尔关于形式和内容以及同一假说的不同表达的谈论是由于消除掉所涉及的物理模态，并且采用外延逻辑中的有效步骤才显得是有理的。但就讨论中的特殊的模态语境来讲便不是这样。亨佩尔关于“等值条件”的讨论提出两个论证，他说:
确认(或否认)两个等值语句中的一个的任何东西也都确认(或否认)其另一个[9]。
这第一个论证以语义学的考虑为基础，就是说: 逻辑等值的语句对事实作出相同的断定，等等。他的第二个论证则是语用学的，他说:
但如果我们采用一个不满足等值条件的确认概念，那么在某些情况下就可能甚至必须这样地争辩: 语句S1来表达一个给定假说，以此为根据作出预测是正确的科学方法，因为已找到S1的许多确认实例。但(比方说为了演绎的方便)根据一个等值表述S2作出这个预测，便是完全不允许的，因为得不到任何确认S2的证据。这样看来，等值条件必须被承认是任何确认定义的适当性的一个必要条件。[10]
这里因为我们所讨论的是具有(x)(F(x)⊃G(x))形式的假说，我们就是研讨一种很原始的和基本的归纳法，而且也假定所用的谓词都是观察谓词。很可能在这些原始的语境中等值条件是无效的。总之，我们现在暂时把等值条件看作一个未决问题。
亨佩尔根据他的批评作出结论: 尼柯标准不能够是确认的必要条件。但是他又指出: 可以认为它陈述了确认的一个特别明显的和重要的充足条件。“而且如果我们以含有一个变项的全称条件假说为限……那么把一个同时满足它的前件和后件的对象看作确认这样一个假说是完全有理的。”[11]
这时，亨佩尔提醒人们注意同时接受等值条件和尼柯标准作为确认含一个变项全称条件陈述的充足条件所导致的令人诧异的一组推断。他把这些结果称为确认悖论。让我们把这些悖论概括如下:
以一个简单假说和它的换质位陈述为例:
所有的乌鸦都是黑的 (1)
所有非黑的都是非乌鸦 (2)
它们大致有四类不同的实例:
a是乌鸦并且a是黑的 (3)
a是乌鸦并且a是非黑的 (4)
a是非乌鸦并且a是黑的 (5)
a是非乌鸦并且a是非黑的 (6)
根据尼柯标准和等值条件，下列陈述成立:
(一)实例(3)的观察确认(1)，但对(2)中立。
(二)实例(4)的观察否认(1)，也否认(2)。
(三)实例(5)的观察对(1)和(2)中立。
(四)实例(6)的观察确认(2)，但对(1)中立。
(五)如果假说的一个表述被观察确认，它的任何逻辑地等值的表述也就被观察所确认。
(六)(1)和(2)是逻辑地等值的。
陈述(一)和(四)违反(五)和(六)，因为同一实例确认两个等值假说中的一个，而不确认另一个。这是第一个乌鸦悖论。要消除这个悖论，我们可以把“确认实例”定义为任何非否认实例。赖特(von Wright)就是这样下定义的。他指出只有实例(4)是假说(1)的否认实例。既然其他各类实例都不否认假说(1)，“我们可以仅仅根据这个理由，说它们提供了这一概括的确认实例”[12]。下面将要看到，亨佩尔也采取同样的定义。但如果把实例(5)的观察看作确认(1)，那么，观察到例如一块黑板、一只黑天鹅、一只黑皮鞋等等，都使“所有的乌鸦都是黑的”被确认。同时根据等值条件，也使“所有非黑的都是非乌鸦”被确认。这是一个很违反直觉的结果，这就是第二个确认悖论。再如果认为实例(6)的观察确认(1)，而实例(3)的观察确认(2)，那么观察到白鞋、红鲱鱼、青菜等等便会使“所有的乌鸦都是黑的”被确认，而观察到一只黑乌鸦也会使“一切非黑的都是非乌鸦”被确认。这样的结果也是违反直觉的，这就是第三个确认悖论。
在考察亨佩尔对这些悖论的评价之前，让我们先看看他对预测标准的反对理由，然后转到他自己提出的标准。亨佩尔把预测标准表述如下:
设H是一个假说，B是观察报告，即一类观察语句，那么
(a)如果B可分为两个相斥的子类B1和B2，使B2不是空类并且B2的每个语句都能够由B1和H的合取，但并不单独地由B1逻辑地导出，那么我们就说B确认H。
(b) 如果H和B逻辑地相矛盾，我们就说B否认H。
(c) 如果B既不确认H，也不否认H，我们就说它对H中立[13]。
应用这个标准于我们的假说(x)(F(x)⊃G(x))，我们便发现F(a)∧G(a)和～F(a)∧～G(a)将是确认实例; F(a)∧～G(a)将是否认实例; 而～F(a)∧G(a)则是中立的。根据上面提出的三种建议把(x)(F(x)⊃G(x))的实例分为正面的( +)、反面的( -)或中立的(0)，如下表所示:
当然上面所表述的预测标准还适用于全称概括之外的假说，所以上面的分类表并不反映它的全部力量。然而值得注意的是，在全称概括领域中，预测标准同当作充足条件的尼柯标准加上等值原则所得结果不一致。因为预测标准也满足等值原则，它们两者在第一、第二和第四实例中是一致的。
亨佩尔对预测标准提出几个反对理由。首先是预测标准并不包括一切科学假说。它不能应用于存在陈述或含有混合量词的陈述(在这一点上和尼柯标准一样)。更重要的是它似乎不适用于用理论谓词而非观察谓词来表述的假说，因为预测标准谈到由有些观察陈述加上假说演绎出其他观察陈述来。但亨佩尔并不认为理论语言和观察语言之间的联系是这么简单的。假说和理论在观察报告之间建立逻辑联系的方式，要比演绎推理复杂得多。他详细地论证这些联系的建立往往以确认为先决条件，因此预测标准不能够是确认的普遍标准。其次，亨佩尔指出: 虽然预测标准满足等值条件，它并不满足特殊推断条件:“如果一个观察报告确认一个假说H，那么它也确认H的每一推断。”亨佩尔相信特殊推断是直觉地可信的。应当把它作为“确认实例”的任何合适定义的一个标准。毕竟一个陈述的逻辑推断或者是等值的或者较弱，它有和原陈述同样的“内容”，或是其“内容”的一部分。如果我们确认全部，就更有理由确认其部分了。并且亨佩尔清楚地证明我们不能够同时接受特殊推断条件和逆推断条件。因为如果那样，确认任何东西的任何陈述就会确认一切陈述，假定a确认p，那么根据逆推断条件它确认p和q(p是p∧q的推断，所以p∧q便是p的逆推断)。然后根据特殊推断条件，它确认q。因为预测标准违反一个恰当性标准，并且满足一个“不恰当条件”，所以要把它拒斥。
但虽然特殊推断条件确似有理，我们接受它为一个恰当性条件时仍必须十分慎重，因为“确认实例”和一堆杂七杂八的概念有松散的联系。如果“确认实例”的意思是: 这个实例本身提供的证据使假说的概率比仅仅根据重言式证据而得到的概率更高些(在亨佩尔论文中可作这样解释)，那么特殊推断条件是假的。因为一个实例可以确认陈述p而不确认它的推断p∨～p。后者根据重言式证据估计有概率1，因而这个概率不能够由于给证据基础添加一个陈述而提高。逆推断条件也能够被证明是假的。因为任何假说p都有一个推断(p或者q)，而q可指任何东西。所以确认(p或者q)的任何东西都会确认p。如果(p或者q)根据重言式证据的概率小于1，q将确认它。这样q就将确认p。但q是和p不矛盾的任何陈述。因此逆推断条件也导致荒谬结果。
这两个流行的确认实例标准既成为不必要的，让我们看看亨佩尔自己的建议。他对上述两个标准进行批评的结果，认识到要给充分令人满意的科学语言下一个“确认实例”定义是很困难的。于是他给自己定出一个较简单的任务: 在相对地简单的语言内部提出一个恰当的定义，这种语言的结构属于没有恒等式的初阶谓词演算，其中一切谓词都是观察谓词。把一个观察谓词赋予一个个体常项便是一个原子观察语句。那么一个观察报告可以是这种语句的任何真值函项的复合语句。令假说H对一个有限的个体类C的展开是一个观察报告，这个报告实质上等值于H的恰恰基于C类中那些个体的一切可能的状态描述。例如，对于只含有一个分子a的个体类，假说(x)(F(x)⊃G(x))的展开便是: F(a)⊃G(a)，～F(a)∨G(a)，～(F(a)∧～G(a))。如果由观察报告B导出假说H对B中出现的个体类的展开，我们就说B直接确认H; 如果假说H由其中每一语句都被观察报告B所直接确认的一类语句推导出来，B就确认H。如果观察报告B确认假说H的否定，它就否认H。如果观察报告B既不确认也不否认假说H，它就是对H中立的。
这个定义满足当作充足条件的尼柯标准和等值条件，所以在亨佩尔自己的系统中也出现确认悖论。亨佩尔用下面的办法来应付这种显然的麻烦: 他说确认悖论并不是什么真正的悖论; 就是说，如果你理解它们的真实情况，它们对直觉的违背就消失了。“这种不合理情况的印象并没有客观基础，它只是一个心理的幻象。”[14]为什么是心理幻象呢? 首先，亨佩尔指出，人们错误地认为“所有的A都是B”这种形式的假说只是对A有所主张(说它们是B)，但对非B却什么也没有说，对所有的事物就更没有说什么了。亨佩尔说: “的确‘每一个P都是Q’这种形式的假说，禁止有属性P而缺乏属性Q的任何对象的出现; 就是说，它使无论任何对象都受限制，都属于那些或者缺乏属性P，或者同时具有属性Q的对象类。这样，每一个对象或者属于这一类，或者在这一类之外; 因此，每一个对象(不单是P)或者符合这个假说或者违反它; 并没有不被这一类型的假说所隐含地‘谈到’的任何对象。”[15]
其次，亨佩尔还指出: 在貌似荒谬的确认实例中，我们常常实际上不是对给定证据E单独与假说H的关系下判断(我们不遵守成为每一个确认实例特征的‘方法论假设’，即除E所包括的内容之外我们并无其他对H有关的证据); 相反，我们默认地把H与由E以及当时我们所掌握的其他知识构成的证据总体加以比较。举例说，假定我试图通过检查我的壁橱里面的东西，以便检验“所有的天鹅都是白的”这个假说。我找到一只黑鞋。由此而断言我已经找到一个确认实例确实是违反直觉的。让我们用符号把这个假说记为(x)(S(x)⊃W(x))，并且同意把我将从壁橱抽出来的第一件东西叫做a。可是，亨佩尔会争辩道: 我早已十分清楚并没有天鹅在我壁橱里，所以我已经知道～S(a)。但这就已表明对象a将是一个确认实例，因为～S(a)∧～W(a)和～S(a)∧W(a)都确认这个假说。所以，进一步决定a是一只黑鞋当然就是不相干的了。要是没有什么理由猜想我的壁橱里没有天鹅，那么，决定a并不是非白的天鹅就的确是相干的和确认性的。
亨佩尔就这样地解释掉这个悖论。这使他好像陷于另一个更坏的悖论。继续研究并不会提高我壁橱里的东西的确认值。因为关于它们不是天鹅的从前知识已经使它们具有确认性了。真的这样吗? 我们可以同意这种知识表明我壁橱里的对象不能够证伪这个假说，但说它们因此就确认这个假说，我们就要犹豫了。难道每一个对象必定或者确认或者证伪任何全称概括吗?假定在缺乏任何背景知识的情况下，我们碰到一个白色的对象，那么这个对象确认一切东西都是白色的这个假说，更不必说它确认了一切天鹅都是白的这个假说[16]; 用同样的推理，如果在缺乏任何背景知识的情况下，我们看见一个非天鹅，这个对象就确认每一个对象都是非天鹅，并没有任何天鹅，更不必说确认了下面这个逻辑推断: 一切天鹅都是白的了。于是或者是非天鹅或者是白色的任何东西都确认这个假说。
让我们更仔细地检查上面的论证。它以十分清楚的形式展示出黑鞋例子的剩余的违反直觉性。因为它表明特殊推断条件同标准逻辑一起就迫使我们接受下述原则: 任何东西是一个全称条件陈述的空洞(并无所指)的证据，便也是这个条件陈述本身的证据。例如，一个非天鹅便是“一切天鹅都是——”这个形式的条件陈述［即: (x)(如果x是天鹅，x就是——)］的证据; 因而便是“一切天鹅都是白的”(以及“一切天鹅都是黑的”，“一切天鹅都有龅牙”，等等)的证据。(亨佩尔并不讨论在给定已知有天鹅的情况下一只黑鞋的确认值。因为他只关心这个实例相对于重言式证据所带来的概率提高，这样，亨佩尔的“方法论假设”并不简单地是卡尔纳普的全证据要求。)但关于有属性F的个体不存在的证据决不是P(x)(F(x)⊃G(x))这个定律的证据。例如，“点质量并不存在”这个命题的证据并不确认斯基尔姆斯所解释的万有引力定律: 任何两个点质量之间相互的吸引力与它们之间的绝对距离成正比。这样看来，在句法上相反对的全称条件概括［例如(x)(F(x)⊃G(x))和(x)(F(x)⊃～G(x))］是归纳地相反对的; 就是说: 即使我们有好证据表明并无当作F的范例的x，它们也不能够同时被归纳地辩护。
上述评语就为古德曼关于应付这些悖论的建议作了准备: “这个［建议］以下述意见为基础: 逻辑上等值的陈述一般并不具有相同的或逻辑上等值的反对陈述，所以，同等地满足各个逻辑等值陈述的［观察］报告，在它们淘汰可供选择的假说的方式上可以仍然是不同的。”[17]试看下表:
逻辑等值的假说 它们的反对陈述
(1)(x)(F(x)⊃G(x)) (x)(F(x)⊃～G(x))
(2)(x)( ～G(x)⊃～F(x)) (x)( ～G(x)⊃F(x))
观察报告
(a)F(a)∧G(a)
(b) ～F(a)∧G(a)
(c) ～F(a)∧～G(a)
(d)F(a)∧～G(a)
让我们用“正面实例”一词来描述满足亨佩尔标准的观察报告。(a)、(b)和(c)都是(1)和(2)两者的正面实例; (d)则使(1)和(2)两者都被否认。然而，(a)不仅是(1)的正面实例，它也使它的反对陈述被否认，虽然并不使(2)的反对陈述被否认。的确，它倒是(2)的反对陈述的一个正面实例。同样地，(c)是(2)的一个正面实例，但否认它的反对陈述; 同时也是(1)及其反对陈述两者的正面实例。最后， (b)是(1)和(2)两者以及它们的两个反对陈述(都是空洞地满足它们)的正面实例。这样，“我们需要区别……简单地同一个陈述一致的证据和同它一致但并不也同它的反对陈述一致的证据……也可以进一步提出:一个假说的确认也许独特地包括以这个方式支持它而不支持一个反对假说的情况”。[18]
这样，按照这个建议，(a)便确认(1)，但不确认(2); (b)便既不确认(1)，也不确认(2); (c)便确认(2)但不确认(1)。恰如按照尼柯标准所得到的结果。因此，如果我们接受这个建议，我们必须认真地对付亨佩尔赞成等值条件的论证。
亨佩尔在为等值条件辩护时，提到定律在科学说明和预测中的作用。假定关于(1)你所掌握的唯一正面实例就是(b)型和(c)型(即空洞地满足它的实例)的观察报告; 那么如果给定初始报告F2难道你会有信心用(1)来预测G2，或者根据(1)和F2来说明G2吗? 我想不。要点在于: 如果我们要使我们关于确认的讨论在亨佩尔所要求的那个原始的(即不考虑背景知识的)水平上进行，那么我们也应当在同一水平上对等值条件进行评价。我们不可以简单地注意到(1)和(2)在某些语境内好像是可以互换的，同时却隐瞒这个事实: 在那些语境内我们已经掌握了许多背景知识; (a)型的许多实例和(b)型的许多实例就构成这种背景知识的一部分。
2．2 解决亨佩尔悖论的各种企图
近四十年来，分析哲学家提出各种各样解决或消除这些悖论的建议。这些建议可以大别为两类。第一类可总称为形式主义者的解决试图，他们主张对科学假说确认的描述不能够违反基本逻辑。所以如果它好像违反逻辑，那么或者这个描述不完全正确，或者所用的逻辑不是十分基本的。因此他们或者提出确认的新解释，或者把逻辑加以修改，以便科学理论(或假说)的辩护成为形式地无矛盾的和直觉地可信的，亦即消除了一切悖论。简言之，形式主义者认为悖论并不是真实存在，不过是由坏的哲学所导致的不幸的和可以避免的结果。这一类形式主义的解决又可分为按照标准逻辑的和修改标准逻辑的两个类型，下面再作简要介绍。
第二类解决试图采取完全不同的立场。近来有为数比第一类少得多的哲学家承认亨佩尔悖论是科学方法和形式逻辑不一致的征候，它起源于哲学家把两者混淆起来，力图使科学方法完全遵从形式逻辑的推演。这些哲学家相信假说的确认在本性上是回避基本逻辑的，因此并不需要严格地遵守等值原则。在他们看来，这些悖论与其说表达了有待解决的困惑，不如说表达了有待研究和理解的生活中的事实。
2．2．1 形式主义的解决
第一类型的形式主义解决试图用并不反对等值原则的其他形式标准来补充或代替尼柯标准。Hosiasson-Lindenbaum、Alexander、Mackie和Pears等人的解决都属于这一类型，我们现在只用冯·赖特的解决作为例子来说明。赖特提出下述问题: “可能用例如黑鞋子或白天鹅来真正地确认所有的乌鸦都是黑的这个概括吗?”答复是: “这究竟是可能的还是不可能的，要随这个概括的‘相干范围’(range of relevance)是什么、这个概括是‘关于’什么的而定。”[19]赖特接着指出，一个概括的相干范围从这个概括本身是看不出来的。因此什么对象提供真正的确认，什么对象提供悖理的确认，也是不清楚的。必须指定范围，才能回答这个问题。范围的指定不同就会导致许多不同的概括。当“所有的A都是B”这个概括的范围没有指定时，它通常就被理解为是关于A类的概括，A类对象便是它的自然的相干范围(naturalrangeofrelevance)。举例说: 所有的乌鸦都是黑的这个概括，当它是关于乌鸦并且仅仅是关于乌鸦的，和当它是关于鸟和仅仅是关于鸟的，和当它是——如果可能的话——无限制地关于世界上一切事物的，便各是一个不同的概括。作为关于乌鸦的概括，和它相干的只是乌鸦，天鹅是不相干的。作为关于鸟的概括，天鹅是相干的，但鞋子却不相干。而作为关于一切事物的概括，一切事物都和它相干。如果它的范围没有指定，通常便把它了解为是关于乌鸦的概括，而不是关于鸟或关于动物或关于一切事物的概括。
这样，赖特用相干范围的概念来解决下面这个悖论: 任何非A的东西都确认一切A是B。他指出: “属于一个概括的相干范围之外的东西可以说对这个概括所提供的仅仅是‘空洞的’或‘虚假的’或‘悖理的’确认，而不是真正的确认。”[20]
关于另一个悖论，即尼柯标准和等值条件的冲突，他是这样解决的:在一个概括的自然相干范围内部，真正确认实例的类是由尼柯标准决定的。“在这个范围之内，尼柯的确认标准是必要和充足的。”[21]一般说，相对于同一相干范围，(1)“所有A都是B”和(2)“所有非B都是非A”是同一概括。但以A为相干范围的(1)和以非B为相干范围的(2)，却是两个不同的概括，因为它们的“自然范围”是不同的。但在另一个指定的相干范围内，(1)也可以被～A∧B或～A∧～B所真正地确认，例如以鸟为范围的概括“所有乌鸦都是黑的”和关于鸟的概括“所有非黑的东西(意指非黑的鸟)都是非乌鸦”，便有相同的真正确认实例。特别是，如果两个概括的相干范围是任何的事物，那么给一个概括提供确认实例的每一事物也给另一个概括提供确认实例，反之亦然。这样一切确认便都是“真正的”，无一是“悖理的”。
上文谈到的古德曼—谢弗勒的解决: 由于逻辑等值的假说不一定导致相同的反对陈述这一事实而避免了悖论，也是属于同一类型的解决。
另一类型的形式主义解决保留尼柯标准，但试图修改传统的二值逻辑或用新逻辑代替传统的逻辑而作为科学推理的更恰当的语法。按照这个语法，假说H并不逻辑地等值于它的换质位陈述(所有A都是B 并不逻辑地等值于所有非 B 都是非 A)。例如，贝尔纳普(N．D．Belnap)和斯托纳克(R．C．Stalnaker)都提出新的条件联结词以代替标准逻辑的实质蕴涵。又如晁天(L．Chao Tien)用三值确认逻辑来代替传统逻辑作为科学辩护的语法。斯基尔姆斯的解决也属于这个类型。他强调科学研究中有待确认的假说是类律性的(lawlike)，并不是一般的概括。用符号来表示便是P(x) (F(x) ⊃G(x)) 或者F →—□ G，而不是(x)(F(x)⊃G(x))。他指出: 虽然两个假说是语义地等值的［例如P(x)(F(x)⊃G(x))和P(x)( ～G(x)⊃～F(x))］，但它们可以不是语用地等值的，而这种语用上的区别可以反映在不同的作证标准中。[22]而所谓语用上的不等值，就是指在科学预测和说明中所起的作用不相同。可见斯基尔姆斯已经从科学方法论观点来考虑这个问题。他的看法似乎是: 尽管从标准逻辑来看，等值原则是必须遵守的。可是在逻辑上等值的陈述，从科学方法来看未必等值。因此，关于类律性假说的确认，尼柯标准仍然适用，不至于同等值条件发生冲突。这样，就可以避免违反直觉的归纳结论。斯基尔姆斯的观点已经很接近于下面要论述的第二大类的解决试图了。
2．2．2 科学方法论的解决
这一类解决的最早尝试是威尔逊(P．R．Wilson)的《论确认悖论》和朱迪思·舍恩堡(Jvdith Schoenberg)的《观察确认和乌鸦悖论》。威尔逊认为在科学假说的辩护中，等值原则是不相干的。等值原则(即: 如果观察确认假说的一个表述，它们便确认任何逻辑地等值的表述)对于全称逻辑命题确实是真的，但像(1)“一切乌鸦都是黑的”和(2)“一切非黑的都是非乌鸦”这样的有待确认的科学假说，却不一定是等值的。他的结论是: 只当(1)和(2)是普遍地真的陈述，才能够断定等值原则对于它们是先天地真的。因为普遍地真的陈述并不需要确认，除非(1)和(2)被当作有待检验的科学假说，否则就根本没有什么确认悖论。但在辩护科学假说的情况下，等值原则并不适用。所以这个悖论便这样得到解决。因为如果(1)和(2)是逻辑陈述，便不发生归纳确认问题; 如果它们被看作归纳假说，它们便不是在确切的归纳意义上等值的。[23]
舍恩堡对乌鸦悖论也采取相同的看法。这里关键的陈述是等值原则。舍恩堡指出:某些观察确认某个假说，这是一个经验标准，而等值原则却要求我们以命题之间等值关系的形式演绎为根据，接受它的后件(“……它们便确认任何逻辑上等值的表述”)中“确认”一词的使用，这样这两个“确认”便没有相同的意义。如果假定等值原则也自动地符合这个经验标准，那便很难理解确认关系的这种传递方式如何能够具有任何形式逻辑的必然性。“因为它的概念属于经验科学方法论，并不属于形式逻辑。”[24]如果逻辑地等值的命题之间有任何差别会使一种经验地下定义的确认关系对于等值命题并不总是传递的，那么等值原则不过是从形式观点提出的给确认下定义的一个不同条件。它不可能具有下面这种意义上的必然性，即: 经验确认必须以如此方式下定义，以便它对于逻辑地等值的命题是传递的。问题倒在于: 等值原则作为给确认下定义的一个条件对经验科学是否有用。[25]
在科学实践中，我们用观察来确认“一切乌鸦都是黑的”和用观察来确认“一切非黑的都是非乌鸦”时，我们分别提出了不同的问题。要辩护第一个归纳结论，需要观察足够多的乌鸦; 要辩护第二个归纳结论，需要观察足够多的非黑的东西。因为这两个假说在它们的名词的指称方面是不同的，所以，如果经验地下定义的确认关系必须涉及名词的指称的话，便不能够简单地假设这个关系对于这些假说是传递性的。由于这些命题的名词所指称的是不同的对象，它们便是不同的命题，虽然它们是逻辑地等值的，即由其中之一可以推出其他的命题。必须区别观察所实际确认的东西和由推理得出的东西，后者仍然要受观察检验。这个要求不仅适用于间接推理，也适用于直接推理。总之，科学家在科学实践中所使用的经验标准，使他们能够把确认直接推理前提的一组观察同确认它的结论的另一组观察清楚地区别开来，例如把F(a)∧G(a)同～G(a)∧～F(a)区别开来。而等值原则却导致这个推断: 不可能把确认两个这样的等值假说的观察区别开来，所以等值原则对于观察确认是一个不可接受的条件。
舍恩堡得出这样的一般结论: 经验标准对于决定哪些观察结果确认哪一个逻辑等值的假说，永远是充分的。可以这样地陈述: 给定一个被观察所确认的假说和它的换质位推论，确认前者的观察并不确认它的换质位命题，反之亦然。所以“一切乌鸦都是黑的”这个假说的确认不能够依赖黑鞋、白天鹅等等观察资料，这些资料和黑乌鸦的实例不同，并不是支持这个假说的证据。它们只是相容(Compatible)实例，并不是确认实例。相容实例既不确认这个假说，也不否认这个假说，但这并不是说，相容的观察在科学推理中不起任何作用。恰恰相反，相容的观察为提出一个观察性假说确立它的预先条件。相容的观察也使科学家可以继续保持这个假说。舍恩堡认为确认和相容性的区别是真正关键所在。
概括地说: 舍恩堡从科学方法的观点作出以下几个结论: 第一，等值原则作为确认的条件是不可接受的; 第二，必须严格区别真正的确认实例和相容实例; 第三，但相容实例并不是不相干的或中立的，它在某种意义上也和确认问题有关。由于放弃了等值原则的条件和主张确认与相容性的区别，这就防止了确认悖论的出现。
蒯因和柯恩(L．J．Cohen)解决确认悖论的方法是把一个假说被确认的方式，即确认方法，同被确认假说所获得的东西，即置信(credence)或归纳支持(柯恩用语)严格区别开来。蒯因和柯恩都是通过下述论证来解决乌鸦悖论的:
(1)确认方法来源于不能形式地描述的基本概念，并且仅仅是某些假说所享有的。
所以
(2)假说之间的形式等值对于它们的相互的可确认性是不相干的，而且并不保证它们有相互的可确认性。
这个论证同上述威尔逊和舍恩堡否定等值原则对确认的作用的论证相类似。但他们还进一步主张:
(3)归纳支持一旦获得，使对它作形式的解释，结果使一个被确认假说的各个等值表述都享有同等的置信度。
蒯因强调(1)和(2)，仅仅附带地提到(3)。另一方面柯恩主要讨论(3)，虽然他也仔细地描述(1)，但对它的起源并不提出分析或说明。尽管有不同的注重点，他们两人都是清楚地按照上述方式进行论证的，至于这个论证本身，(1)当然是关键。如果能够给(1)提出有说服力的论证，那么亨佩尔悖论就毫不足道地避免了。因为黑乌鸦是否能够确认“乌鸦假说”是一个方法问题，因而无需根据等值原则去讨论。既然(2)由(1)得出，并且没有人对(3)提出异议，下面我们将集中论述(1)。
蒯因指出本体论上被断定的类有两个根本不同的类型。首先，对象被认识并且按照相同性与类似性的固有标准被直接地归入各(自然的)类(例如红的东西、乌鸦、爬虫、等等)。使用我们的逻辑工具我们还能够进一步分类(例如非红的东西，是乌鸦或是爬虫的东西，等等)。但后面这些类与相似性或相同性无关，也非直接分类的结果。蒯因称之为非自然类。这样，使用实例仅仅是对自然类作概括的基础，而非自然类则是在前已形成的自然类的基础上组成的。其次，逻辑等值并不保持自然性。虽然A⊃B逻辑地等值于～B⊃～A，A和B是自然类这个事实并不蕴涵～A和～B也是自然类。蒯因甚至似乎认为A的自然性蕴涵～A的非自然性。这就是蒯因讨论悖论的基础。
像乌鸦假说之类的简单概括断定A类的所有分子属于B类。蒯因虽然不阐述科学方法论，却提出尼柯标准的一种非形式的型式:
就一个假说被确认而言，使它得到确认的是它的预测的证实。特别当这个假说是一个由归纳得来的概括时，那些预测便简单地是概括的实例。这样确认一个归纳的便是它的实例。[26]
如果A和B是自然类，那么正如我们当初用直接挑选、用实例来处理A和B那样，也应当以相同方式来处理: “所有的A都是B”。因为乌鸦a和b是被计算在乌鸦类之内的，黑的对象c和d是被计算在黑对象类之内的，所以我们感受到在肯定乌鸦是黑的而进行分类时，应当把黑乌鸦计算在内。但是如果A和B是非自然类，即不是由归类得来的，对于断定这个假说正如对于当初A和B的分类一样，例证是不相干的。
这样，当我们认识到实例作证(尼柯式的确认)对于“所有的乌鸦都是黑的”(“乌鸦”和“黑的”都是自然类)虽然相干，对于下面这个非自然的换质位陈述“所有非黑的东西都是非乌鸦”却是完全不相干的; 那么尽管从逻辑观点来看这两个假说是等值的，确认悖论就不再成为问题了。(构成“乌鸦假说”的其他两个等值陈述当然也是如此。)
但蒯因的解决还进了一步。上面提到的第三个悖论不仅包括大家纷纷讨论的用白鞋子、红鲱鱼来确认“所有乌鸦都是黑的”的荒谬，这可以叫做问题-1; 声称搜集黑乌鸦便可以确认”所有非黑的东西都是非乌鸦”也是同样违反直觉的，这叫做问题-2。蒯因的方法避免了这两个问题。因为不自然的换质位陈述像任何其他不自然的假说那样首先就是不适宜于用实例来确认的。辩护方法是基本的，溯源于非形式的因素，本身就是不遵从等值原则的。置信却是另一回事。它是由这个方法所给予的，但并不源出于这个方法。相反，它是按照形式逻辑的要旨来处理的，以便不再保留在得到它的方式中所含有的非理性因素。
蒯因的论证可以概括如下:
(1)我们所固有的相同性和类似性标准是非形式的和非逻辑的。
(2)种类是借助于这些标准归纳出来的。
(2)种类是科学辩护方法的中心概念。
蒯因的解决对于在确认之前已经被自然化的假说，即一般初等科学中的假说来说，是充分的。但它是否能够外推到成熟的科学推理中呢? 它的中心思想是谓词的自然性(naturalness)。这个思想构成实例作证的非形式性质的基础，也是等值假说之间在辩护方法上的区别的基础。但一旦科学发展到比非形式的自然性更高的水平，按蒯因的分析，是否又会再次把悖论引进来呢?
柯恩在其著作《归纳的蕴涵》(Implicationsof Induction，1970)中提供对科学辩护的一种可避免亨佩尔悖论的充分说明，并且其论证同蒯因的基本论证大致一致。但它更适宜于成熟的科学推理。所以如果把蒯因和柯恩的说明结合起来，我们就会得到比较全面的解决。柯恩关于确认悖论的处理可以这样地概括:
……等值原则仅仅适用于有关支持的陈述，而不适用于有关检验结果的陈述。如果U1和U2是等值的，那么对U1的支持永远也是对U2的支持，但对U1的一次检验并不永远也是对U2的一次检验。关于亨佩尔悖论的困惑的一个来源就是“确认”这个动词有一种使正面支持和有利的检验结果之间的区别模糊起来的方式，它把这个重要事实掩盖了。[27]
柯恩把置信度即归纳支持，与置信度借以分配的确认过程即检验严格地区别开来。检验是仅仅对某些假说作出的，因而它并不遵守等值原则。但什么是检验所导源的、使它的非形式性质得到说明的基本概念呢?
柯恩是一位方法论的证伪主义者。对他来说，科学辩护可以叫做试图证伪的努力。寻求这种证伪——这就是检验方法本身——是不遵守等值原则的。例如要检验“一切无翼者皆不飞行”的假说，便应当在无翼者当中寻找飞行的; 但如试图证伪“一切飞行者皆有翼”却应当检查飞行者是否有翼。虽然这两个假说是逻辑地等值的，但它们的检验方法却不相同。这就是柯恩所要探讨的问题。
他说，检验一个简单概括，例如“乌鸦假说”，就是要调查研究是否有不黑的乌鸦会被发现。单纯地把黑乌鸦堆集起来并不是这个假说的检验，除非在这样的环境中，即在乍看起来我们有理由相信容易使乌鸦改变颜色的环境中检验乌鸦的黑色。这就是从前的经验很有干系的地方。“谨慎的实验家”将尽可能严峻地检验他的假说，这就是说他将在这个假说有效的可能性最小的时间、地点和条件下进行检查。但是他的关于在什么环境中进行反驳最可能取得成功的知识，是由从前类似的成功反驳中获得的。他将在类似的鸟过去曾被发现改变了颜色的那种环境中检验乌鸦的黑色。这里过去经验所起的作用，并非为该假说辩护，而是为我们的检验方法辩护。这样，适宜于经验检验的每一假说都有环境变项(季节、年龄组、地理位置、一天内的不同时刻等等)的一个有限类。类似的假说在过去被证伪时曾有这些变项的一定变式出现，而当其他的变式出现时相同的假说就有正面的例证。这后一个条件是重要的，因为它确证在证伪时出现的这一变项的变式，部分地构成证伪的原因。柯恩对乌鸦悖论的解决的核心是下述事实: 在逻辑等值的变形中因果关系箭头是不传递的。过去亨佩尔等人指出: 悖论的感觉源于没有加以考虑的潜在背景知识的出现，一旦或者合适地把它忽略掉，或者明显地把它纳入形式系统中，悖论就消失了; 柯恩的论证也许使人感觉到和这些意见相似。在某种意义上确是如此。但对柯恩来说，背景知识构成对确认过程进行分析的基础;而对形式主义者来说，确认同背景知识没有任何关系——确认是要不顾知识而被分析的东西，确认不过是把命题之间的形式关系应用于背景知识，或与其相结合。形式主义的特征就是简约为空洞无物。相反，对蒯因和柯恩来说，缺乏任何知识而谈知识的增长是没有意义的，对蒯因来说，归纳本质地涉及本体论上先有的归类。对柯恩来说，它预设一个有组织的科学研究的范围。对两人来说，形式主义的严酷而贫瘠的园地并不提供研究科学方法的立足点。
“季节变换使有些动物改变颜色; 它并不使一些有颜色的东西改变它们所隶属的动物种类。”[28]虽然“所有的野兔都是灰色的”逻辑地等值于“任何非灰色的东西都不是野兔”; 虽然接受或拒斥一个便是接受或拒斥另一个; 虽然一个不灰的野兔便是这两个假说的潜在证伪者; 但通过设计和选择能够引起野兔变色的环境来寻求不灰的野兔——也就是检验“所有的野兔都是灰色的”——是一回事，而试图把一个不灰的东西变成野兔，亦即检验那个换质位陈述，却是完全不同的另一回事。后者显然是不可检验的。柯恩清楚正确地指出: 环境情况变项表是由检验相似假说的过去经验中产生的。但他未能够指出: 可检验性本身也是类似地归纳得来的，并不是形式地产生的。可检验性取决于在寻求潜在证伪者时这两个谓词中的哪一个(“乌鸦”还是“黑的”)被利用。你把乌鸦性固定起来去寻求非黑性呢，还是把非黑性固定起来去寻求乌鸦性。重要的并不是乌鸦对于黑的或非黑的东西的相对数量，重要的是我们已有的关于世界的知识，就是说改变颜色的是鸟，却并非改变物种的是颜色。同样地，可检验性并不以有关谓词的自然性为转移; 乌鸦性是固定的而黑色是可变的，这一点并不表示“乌鸦”比“黑的”是更基本的牢固的种类。“一切飞行者都有翼”和它的换质位陈述“一切无翼者都不飞行”以及两者的不同的检验方法便证明了这一点。检验方法在于已经预先有了关于潜在证伪者如何“显露出来”以及关于它们最可能出现的环境的想法，所有这一切都是我们由过去成功地证伪类似假说的经验中学习到的。
柯恩的论证可以概括如下:
(1)(严肃的)试图发现非黑乌鸦的努力归于失败，便使“乌鸦假说”以及它的一切等值表述获得归纳支持。
(2)寻找非黑乌鸦的途径是在据认为有利于它们羽毛颜色改变的一切环境中观察乌鸦。
因此:
(3)在这样的环境中发现的黑乌鸦便构成失败的证伪，它提供对乌鸦假说的支持，而在同样环境中发现的非黑的非乌鸦则否。
(1)、(2)和(3)都是合理的，并不留下任何悖论的残余。
正如我们所见到的违抗等值原则，从而产生明显的悖理性的正是经验的检验方法本身。一个科学家使他的假说能够受到的最严峻的检验，是在科学共同体相信最可能成功的地点、时间和情况中，而不是任意地寻求证伪。然而，毕竟这种科学“预感”归结起来就是关于相同性和种类的想法。柯恩关于这种猜测的相同性与种类的想法可适用于科学理论结构内部，同科学自身被组织为各个研究领域的方式有密切关系。这种“谨慎的证伪主义”保证科学知识能够脚踏实地前进。如果在偶然的观察中碰上一只灰乌鸦，“乌鸦假说”将被反驳，但这对于作为出发点的理论结构并无反馈作用; 正如偶然地发现一只黑乌鸦，对证伪主义者来说，对于这个假说并不产生反馈作用一样。另一方面，如果灰乌鸦是在理论所预测的情况中被发现的，这个假说同样地被证伪，但这一次导致它被修改的是先已被证认的理论。反之，在反驳不成功的情况下，这个新近被证认的假说就会促使鸟类学家重新考虑他的初始理论，例如认为乌鸦和天鹅在羽毛颜色方面会发生相似变化的假设。所有这一切会导致产生关于相同性的新假设，从而导致对乌鸦进行新的检验。
我们关于周围世界的知识是在各个不同层次上累积起来的。在常识层次上，知识的学习和增长大致按照蒯因所描述的方式进行，就是运用我们所固有的相同性与种类的标准。在较高的学习层次上，知识被猜想、推测，并在仍然与相同性和种类的想法有关的已获得知识的基础上付诸检验。这些想法像固有标准一样是同等地自然的，但被应用于假说而非应用于对象，从而允许对不相似的对象合理地加以研究。这就是柯恩关于知识增长的观点。其结果，科学永远具有未被反驳的知识作为不断前进的基础。这样蒯因和柯恩便从科学方法论观点说明了科学知识是怎样获得和怎样增长的，从而避免了形式主义者难以解决的确认悖论。
现在我们把关于确认悖论的讨论概括为以下几点:
1． 按照尼柯标准，确认一个假说(x)(F(x)⊃G(x))的实例并不确认这个假说的其他逻辑地等值的表述，例如，(x)( ～G(x)⊃～F(x))。这是第一个确认悖论。
2． 亨佩尔试图给“确认实例”下一个可以避免上述悖论的定义。他把一切和假说相容的实例都看作确认实例，这样便满足了等值原则，但却导致悖理的推断，即不仅黑乌鸦确认了“所有乌鸦都是黑的”，一切非黑的非乌鸦(例如白鞋和红鲱鱼)都使乌鸦假说被确认。这就是引起广泛讨论的“乌鸦悖论”。［上文称为“第三悖论”。类似的第二悖论是: 任何非乌鸦都使乌鸦假说或它的等值陈述(“所有非黑的都是非乌鸦”)被确认。］亨佩尔却主张这个推断可被接受，其貌似悖论的性质应归因于人们的心理幻象。赖特也采取和亨佩尔相同的确认实例定义，却试图以另一方式来解决悖论。
3． 古德曼和谢弗勒不同意亨佩尔的结论，提出解决这些悖论的新建议。逻辑上等值的陈述往往各有不同的或不等值的反对陈述。一个假说的确认实例不仅要和假说相容或一致，它还必须淘汰其他可供选择的假说。这样，一个确认实例应是同这一假说一致但同它的反对陈述不一致的实例，亦即支持它而不支持这个反对假说的实例。按照这个建议便会得到按照尼柯标准所得到的相同结果。
4． 以上各种解决悖论的努力都属于形式主义的类型。形式主义者坚持科学辩护方法和形式逻辑的一致性，科学辩护决不能够违反形式逻辑。他们或者主张严格遵守等值原则，从而像亨佩尔那样认为违反直觉的结果是可以接受的; 或者对标准逻辑进行修改，以便避免明显地违反直觉的结果。例如斯基尔姆斯指出: 虽然乌鸦假说和它的换质位陈述(“所有非黑的都是非乌鸦”)在语义学上是等值的，在语用学上却不是等值的。但在科学辩护问题上，语用学的考虑非常重要，因此，当一个观察报告确认一个假说而不确认它的一个等值表述时，如果两者并非语用学上等值的，就不是违反等值原则。这种从语用学观点出发的解决方案已经很接近于非形式主义的解决了。
5． 非形式主义的或科学方法论的解决方案的主要立场是: 确认悖论是哲学家忽视科学方法论和形式逻辑的区别，力图使科学方法完全遵从形式逻辑的推演的结果。它恰恰生动地表现了科学方法和形式逻辑的不一致或冲突。这一类型解决努力的先驱者是威尔逊和舍恩堡。他们认为在科学假说的辩护中，形式逻辑的等值原则是不相干的。舍恩堡还认为两个逻辑地等值的命题，由于其中名词所指称的是不同的对象，仍然是两个不同的命题。辩护这两个命题要用不同的证据。所以等值原则对于经验确认来说，是不可接受的。其次必须严格区别真正的确认实例和相容实例。由于等值原则的放弃和确认与相容的区别，这就防止了确认悖论的出现。
6． 蒯因和柯恩更进一步辨明科学方法和形式逻辑的不同的范围。他们解决悖论的立足点都是把确认假说的方法和确认过程的结果，即假说的置信或归纳支持严格区别开来。蒯因的论证步骤如下: (1)我们认识世界或从经验中学习时所固有的相同性或类似性标准是非形式的和非逻辑的; (2)事物的种类是借助于这些标准归纳出来的; (3)种类是科学方法论的中心概念。自然类和非自然类的严格区别是解决确认悖论的基础。柯恩的论证方式和蒯因的论证大致一致，他把假说的检验和假说所获得的归纳支持严格区别开来。检验方法是不遵守等值原则的。两个逻辑地等值的假说的检验方法是不同的。关于乌鸦悖论的解决，柯恩的论证步骤是(1)热衷于发现非黑的乌鸦以便证伪“乌鸦假说”归于失败，便使这个假说和它的一切等值表述都获得归纳支持; (2)寻找非黑的乌鸦要在据认为有利于它们羽毛颜色变化的一切环境(这是由已证认理论所提供的知识)中去观察乌鸦; 因此:(3)在这样的环境中发现的黑乌鸦便提供确认实例，使证伪试图归于失败，而在相同环境中发现的非黑的非乌鸦(白鞋，红鲱鱼等等)则不提供确认实例。以上(1)、(2)和(3)都是合理的，并不产生任何悖论。蒯因的论证以谓诃的自然性或非自然性(自然类或非自然类)为基础，更适合于常识的或初级科学的归纳推理; 柯恩的论证以已获得成功的证伪和已被证认的科学理论为基础，更适合于成熟科学的归纳推理。把他们两人的论证结合起来，便构成一幅可说明知识如何获得和增长的、没有留下悖论的、合理的和较全面的图画。
[1] 古德曼: 《事实、虚构和预测》，哈佛大学出版社1955年版，第101～102页。
[2] 《事实、虚构和预测》，第104页。
[3] 卡亨: 《古德曼的巩固论》，《科学哲学》第32卷，第377～383页。
[4] 卡尔纳普: 《论归纳逻辑的应用》，《哲学和现象学研究》第8卷，第133～147页。
[5] 阿克曼: 《品类谓词和确认》，《哲学研究》第20卷，第1～4页。
[6] 弗里德曼: 《绿蓝的信徒: 简单性与巩固性的对立》，《理性》，第7卷，第366～378页。
[7] 斯基尔姆斯: 《选择与机会》，迪肯森出版公司1975年版，第75页。
[8] 亨佩尔: 《确认逻辑研究》，《心》第LIV卷，1945年，第5页。
[9] 《心》第LIV卷，第12页。
[10] 《心》第LIV卷，第12～13页。
[11] 《心》第LIV卷，第13～14页。
[12] 冯·赖特: 《哲学逻辑》，巴·布莱克韦尔出版公司，1983年版，第34页。
[13] 亨佩尔: 《心》第LIV卷，第98页。
[14] 《心》第LIV卷，第18页。
[15] 《心》第LIV卷，第18～19页。
[16] 这是亨佩尔提出的论证。
[17] 引自谢弗勒: 《研究的解剖》，哈佛大学出版社，1963年版，第286页。
[18] 引自《研究的解剖》，第290～291页。
[19] 赖特: 《哲学逻辑》(哲学论文集第Ⅱ卷)，第40～41页。
[20] 《哲学逻辑》，第40页。
[21] 《哲学逻辑》，第43页。
[22] 斯基尔姆斯: 《律则的必然性和确认悖论》，《科学哲学》第33卷，第242页。
[23] 威尔逊: 《论确认悖论》，《英国科学哲学杂志》第15卷，第196～199页。
[24] 舍恩堡: 《观察确认和乌鸦悖论》，《英国科学哲学杂志》第15卷，第201～202页。
[25] 舍恩堡: 《观察确认和乌鸦悖论》，《英国科学哲学杂志》第15卷，第202页。
[26] 蒯因和尤莲(J．S．Ullian): 《信念网》(1970)，纽约，兰多姆出版社，第66页。
[27] 柯恩: 《归纳的蕴涵》，伦敦，1970年版，第101页。
[28] 《归纳的蕴涵》，第98页。