贝叶斯推理
5.1 小引
上述两种经典的统计推理有两个基本假设: (1)概率陈述必须以概率的频率解释为其唯一的基础; (2)样本数据是有待分析的唯一具“客观的”形式的资料。这两个基本假设都受到贝叶斯主义者的批评。即使从上文对估计和显著性检验的各种方法的简述中,也可清楚地看到经典数理统计传统已经发展出多么丰富的统计方法论。但是反对者对这两个基本假设的各种批评并非毫无理由,他们至少明确地指出了经典方法的局限性。
第一,经典推理以基于频率解释的概率概念为唯一根据,这是经典方法的核心。它主张概率模型必须建立于一个样本空间上,并假定这个样本空间可提供对于在与目前所研究情况相同的条件下所进行的反复试验加以研究的恒常基础。这样一个集体(collective)是否存在(即使在概念上),有时是有疑问的; 对这个样本空间的详细说明也许被认为是武断的或者主观的。
第二,经典方法对被它看作“相干资料”的东西大加限制,就是说它认为只有样本数据才是适宜于进行定量化和加以形式分析的。但推理者先已掌握的资料或先验信息(priorinformation)也是有待加工处理的资料的重要部分,特别当这些先验信息也能够容易地进行定量化的时候,对经典方法的批评就更加强烈了。
鉴于经典方法具有一定的局限性,贝叶斯方法是在超越这种局限性的基础上发展起来的。贝叶斯推理是很值得重视的统计推理的新形式,它给归纳逻辑提供了新的发展方向。我们既要肯定经典方法的辉煌成绩,也要明确这种方法并非在任何场合都是同样有效的。而在这些场合,贝叶斯方法特别适用。但贝叶斯方法也适用于其他场合。照目前情况看来,贝叶斯主义似乎提供了关于归纳推理和决策论的一个统一的理论。
5.2 贝叶斯方法
英国数学家贝叶斯(Thomas Bayes)对统计推理的主要贡献在于他使用了“逆概率”(inverse probability)这个概念,并把它作为一种普遍的推理方法提出来。拉普拉斯后来进一步发展了贝叶斯的这个贡献。
贝叶斯定理原来是演绎的概率论中的一个定理,一个演绎的概率陈述。它断定: 已知一个事件集Ai(i=1,2,……,k)中每一Ai的概率P(Ai),又知在Ai(i=1,……,k)已发生的条件下,事件A的条件概率P(A/Aj),就可得出给定A已发生,任何Aj(i=1,……, R)的条件,(“逆”)概率P(Aj/A)。这个贝叶斯定理有很广的应用范围。但作为研究贝叶斯推理的起点,我们必须扩充这个定理的意义,不考虑事件集A,而考虑构成实际情况的一个合适模型的假说集Hj(i=1,2,……,k)。其中一个而且仅仅一个假说必定是真的。事件A则被重新解释为由实际情况得到的观察结果: 样本数据。在观察之前,对所有的i=1,……,k,已知P(Hj)。这些概率是不同假说的先验概率,构成次要的信息来源。又知P(A/Hj)(i=1,……,k)即在Hi真时A被观察到的概率,这些是样本数据的似然(Likelyhood)。这样,我们就能够把贝叶斯定理重新解释作提供一个通过样本数据的使用把我们用先验概率P(Hi)(i=1,……,k)来表达的原来知识状态予以更新的工具,这个校正的评估表现后验概率P(Hi/A)(i=1,……,k),即在我们利用由观察A的发生所提供的新信息后不同假说Hi真的概率。这些后验概率(逆概率)由下列公式得出:
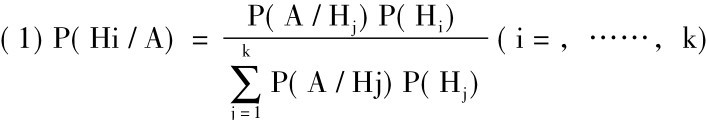
贝叶斯推理的本质就是: 相对于A的Hi的后验概率同Hi的先验概率与Hi真时A的似然的乘积成正比(上式右边的分母不过是独立于i的标准化常数)。关于实际情况的先验信息就这样地加上样本数据以便得出对那个情况的现行概率描述。在这一点上,贝叶斯方法是推理方法。它断定我们的现行知识是被这个后验概率集P(Hi/A) (i=1,……,k)所充分描述的。
公式(1)的一个直接推断提供关于贝叶斯推理的基本原则的复述。假定我们所关心的是两个特殊的假说Hi和Hj。它们的后验概率的比率由下式给出:
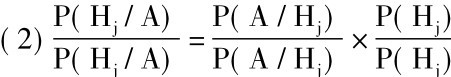
就是说,由它们的先验概率比和似然比的乘积给出。
例1. 一个匣里有相同数目的两类六面的方骰子。就它们的形状、密度等等物理属性来说,这些骰子是完全对称的。第一类有标着1, 2,3,4,5,6的六面; 第二类有标着1,1,1,2,2,3的六面。一个可信的概率模型是规定任何骰子被投掷时露出的那一面都有相等的概率六分之一。由匣里随机地取出一颗骰子,投掷两次,在分别的(独立的)投掷中露出一个“1”和一个“3”。观察到这一点,我们想要推测这颗骰子是第一类的还是第二类的。我们把这两个互斥的可能性称作HⅠ和HⅡ,似乎有理由给它们每一个分配相等的先验概率。于是贝叶斯定理便给HⅠ和HⅡ分别得出后验概率四分之一和四分之三。这个结论是关于基本实际情况的一个推论性陈述。它描述所用骰子属于第一类还是第二类的相对机会分别地是对第二类有利的三比一。按照贝叶斯原来的表述我们便会说: 认为这颗骰子属于第二类的“猜测”有四分之三的概率是正确的。(https://www.daowen.com)
这个例子很好地说明了(1)式中重点的改变。现在贝叶斯定理是关于产生观察数据的不同的概率模型的可信性的陈述,不再是一个演绎的概率陈述了。
在这个例子中,先验概率和后验概率都能够按照频率说来解释,由随机地从包含相同数目的两类骰子的匣子里选出一颗的这个较大实验中,也可以直接导出先验概率的数值。它们的准确性当然依靠我们关于这种实验所作假设: 这颗骰子是由数目相等的两类中真正随机地选出的。似然的估值当然也以选择的随机性和骰子投掷的相继结果的独立性为基础。在这种情况下,主观的先验概率和客观概率一致,对于由贝叶斯定理导出的这个逆概率陈述的解释是毫无问题的。例1是对于在遗传学中真实情况的一个简单但典型的例解。但一般地会发生更复杂的情况,像下述两个例子也是能够在实际情况中找到的。
例2. 一个匣子里有许多分属两类的六面方骰子。就它们的形状,密度等等物理属性而言,这些骰子是完全对称的。第一类骰子的六面标出1,2,3,4,5,6; 第二类的标出1,1,1,2,2,3。匣子里第一类的骰子较之第二类的为数更多。从匣子里随机地取出一颗骰子,投掷两次,在分别的(独立的)投掷中露出一个“1”和一个“3”。关于这颗骰子是第一类的还是第二类的,我们能够说什么呢?
例3. 一位朋友有例1和例2所描述的每类骰子中的一颗,他在这两颗骰子中选出一个,并不说明它属于哪一类,但表示他愿意永远用这一类骰子而不用另一类。他把这颗骰子投掷两次,并且报告结果说,露出的那一面一次是1,又一次是3。关于他所用骰子究竟是哪一类的,我们能够说什么呢?
在例2中,P(Hi)和P(Hi/A)(i=Ⅰ,Ⅱ)仍然可以有相应的频率解释。但是我们现在关于实验设置的知识(第一类骰子较第二类的要多)并不足以给P(HⅠ)和P(HⅡ)分配准确的数值。我们只知道P(HⅠ) >P(HⅡ),就是说P(HⅠ)大于二分之一。用贝叶斯方法来进行推理,我们必须把数值代入P(HⅠ)和P(HⅡ)。怎么办呢? 我们掌握的信息也许会更少,并不知道哪一类占多数。但问题仍然存在! P(HⅠ)和P(HⅡ)的值是什么呢? 我们也许可以把后一情况称为“先验无知”(priorignorance)。要使用贝叶斯方法,我们必须把这个情况定量化。贝叶斯提出的理由不充分原则(theprincipleofinsufficient reason)或无差别原则(theprincipleofindifference)建议: 在并无有利于类Ⅰ或类Ⅱ的证据时,我们可假定P(HⅠ)等于P(HⅡ)等于二分之一。但P(HⅠ)用频率解释是很明确的; 它有特定的值,虽则是未知的。在宣称P(HⅠ)等于二分之一时,我们并不真的主张匣子里两个类型的骰子是数目相等的。我们作出一个关于自己心理状态的陈述;我们不能够找到先天地相信一类骰子较之另一类为多的根据。P(HⅠ)等于二分之一这个陈述所涉及的概率概念已变成一个关于置信度的概念(或者是主观的,或者是逻辑的)。
在例3中,我们关于实验设置所知的就更少了。再次根据理由不充分原则,我们可以配给约定的数值P(HⅠ)等于二分之一,也可使用概率概念的逻辑解释。另一可能,个人意见也许和问题相关。我们也许觉得这位朋友是有点怪癖的,更多地会选择“奇特的”第二类骰子。这种感觉对于为P(HⅠ)赋值的需要有干系吗? 有人会主张这是相干的,便使用P(HⅠ)小于二分之一的值。再次决定赋予P(HⅠ)以哪一个准确的小于二分之一的值便好像有任意性。面对同一问题的另一个人也许把这位朋友看作一个相当“保守”的人,更倾向于选取第一类的骰子。他便会选择P(HⅠ)大于二分之一的值。先验概率现在就需要采取私人的或主观主义的解释,而不采取逻辑的解释了。
一般地说,在贝叶斯推理中,先验概率和后验概率都是按照主观概率,即合理置信度来解释的。在先验概率也能够作频率解释的场合,那便是主观概率和客观概率相符合的并不常见的情况。在其他场合,如何确定先验概率的数值是一个很重要而又困难的问题,这个问题的解决是贝叶斯推理细节中的本质部分。这个问题还有不同看法的争论,还未获得很好的解决。即使在先验信息是由以前对相同实际情况的观察得来的样本数据所构成这样的简单场合,也并非没有困难。这种“经验的贝叶斯方法”也是有问题的,这里暂置不论。
但是,当代的贝叶斯决策论已为先验概率的选择提供了合理的标准,而放弃早期以萨维奇等人为代表的私人主义者(personalists)的这个观点: 先验概率的选择永远仅仅取决于私人的态度,任何选择同任何其他不同选择相比,都不能够是较合理的或者较不合理的。
5.3 先验概率的选择问题
关于如何进行选择的问题可以有两种极端看法: 一种看法是上述的私人主义; 另一种相反的看法被萨维奇称为必然主义观点(necessary views)。按照这个观点,存在着选择先验概率的很明确的标准,而这些标准永远毫不含糊地决定一个特殊的先验概率集合作为我们唯一的合理选择。
较温和的看法认为,以上两种极端看法都是完全站不住脚的。例如,哈桑尼(John C.Harsanyi)指出: 大家公认,在信息极其有限的情况中,我们对先验概率的选择便必然会很接近于私人主义的模式。但是他们认为有选择先验概率的很明确的标准,它们的作用就在于帮助我们在选择先验概率时尽可能最好地利用我们可以得到的情报,但在情报极少或者绝无时它们就无能为力了。
另一方面,当我们得到足够的准确的定量情报时,这些合理标准就成为极其有力的分析工具,并且事实上能够毫不含糊地决定一个合理决策者所能够选择的先验概率。
最后,当然还有许多中间场合。例如有这样的情况,这时所有有理性的人们都同意我们必须给一个给定假说分配略高于(比方说)三分之一的概率,但关于准确的概率值的选择等却可以彼此分歧。
关于先验概率的选择问题是专门的技术性问题,读者在作深入研究时还要进一步阅读程度较高深的专论或专著。
[1] 本节假定个人的确定性模型,绝大多数医师都是这样假定的。如果假定个人的随机模型,那么在初始状态和各个可能的最终状态之间就不再有唯一的联系。
