消除归纳法
4．1 消除归纳法
枚举归纳法由单称前提导致普遍结论。由一个规律性在一定数量的被研究事例中被确认导致它将永远被确认的结论。这种推理的不确实性早就引起怀疑。在这方面，通常认为，如果我们根据一个规律性在若干特定场合被确认，合理地推出这一规律性是普遍有效的，那么我们的推理过程仅仅表面上遵循枚举归纳法的程序; 普遍结论好像只是由单称前提推出来的。人们主张，如果我们之由个别事实导出普遍定律是合理的，那么我们的那个普遍结论所根据的，不仅有陈述这一规律性的特定事例的那些前提，而且还有某些其他的对于使导出普遍结论成为合理程序必不可少的前提。
试看下述例子。我从桌上拿起一根回形针，借助于我从手电筒上拆下来的灯泡和电池，我发现这根回形针是一个良好的导电体。根据枚举归纳法，我能够由这个简单前提作出各个不同的结论。比方说，考虑到这回形针是铁制的，并且是良好的导电体，我能够引出每一铁制对象都是良好的导电体这个结论。但考虑到这回形针是在我桌子上的物体之一，并且是一个良导体，我也能够引出这个结论: 在我桌子上的每一对象都是良好的导电体。对于这两个可能的结论，我采取完全相反的看法。我很有把握地作出每一铁制对象都是良好导电体的结论，但即使我并不预先知道桌子上有些物件不是良导体，我也不愿意作出在我桌子上的每一对象都是良导体的结论。怎样去说明这两个枚举归纳推理的区别呢? 可以从下述事实得到说明: 当我作出一切铁制对象都是良导体的结论时，我所使用的前提不仅是陈述这一个铁制对象(回形针)是良导体的前提，还有下面这个前提: 一切化学成分相同的对象，因而一切铁制的对象，就导电性而论都有相同的性质，因此或者它们的每一个都是良导体，或者没有一个是良导体。这是一个析取陈述: “一切铁都是良导体或者没有铁是良导体”，如果加上单称前提“这个对象是铁制的”和“这个对象是良导体”，那么这些前提否定了这个析取的陈述的第二肢，单单留下第一肢。因此，推理过程是按照下述形式进行的:
每一S都是P或者无一S是P
a是S并且a是P
所以: 每一S都是P
因而我的推理过程仅仅表面上遵循枚举归纳法的形式:
a是S并且a是P
所以: 每一S都是P
这种误解是由于忽略前提中隐含的另一个析取陈述，它的一肢被明显陈述出的单称前提否定掉。
而根据我桌子上的某一对象是良导体推出“我桌子上的每一对象都是良导体”的另一个推理中，我们却不能够提出像上面这样的隐含前提，因而这后一个推理便是不合理的。
定义12: 下述推理称为消除归纳推理: 其中一个前提是n个普遍陈述的析取，其他前提是单称陈述，它们反驳这个析取陈述除一肢外的一切肢，而结论则是唯一未被反驳的那一肢。
它叫做归纳推理，因为它由单称前提导致普遍结论。但必须记得，不同于枚举归纳法，它并非单只由单称前提出发。它还使用由几个普遍陈述的析取组成的另一个前提。但消除归纳推理这一名词是会引人误解的，因为只要这种推理的析取前提和单称前提是充分置信地被接受的，它的结论便逻辑地由前提得出，因而事实上是一种演绎推理。它的要点是: 第一，由单称前提演绎出某些普遍陈述的否定; 第二，由几个普遍陈述的析取以及除一肢外其余一切肢的否定，演绎出唯一不被否定的那一肢作为结论。这个推理的每一步，结论都由前提逻辑地得出，因而实质上是演绎的。使用这种推理，我们能够以主观上充分置信的方式得出结论。
4．2 因果推理
所谓因果推理通常便是采取消除归纳推理的形式。为什么要进行因果推理呢? 因为因果关系的知识在应用上十分重要。这种应用就在于或者通过产生原因以产生预期的结果，或者通过消除原因以消除有害的结果。著名的穆勒方法就是寻求原因的推理，也被称为消除归纳法。在分析这些方法之前，让我们首先对“原因”这个概念略加分析，以便确定我们所要使用的概念的涵义。
“原因”一词在日常应用中有许多不同的涵义。首先，我们可把一个事件的远因和近因区别开来。近因就是在一个给定的原因系列中直接引起该事件的那个原因。对同一事件来说，这个序列中在近因之前出现的一切原因都是远因。其次，我们可以区别易控制的原因和不易控制的原因，这是就人的知识和技术水平是否使我们能够干预某些事件的发生或不发生而作的区别。再次，我们可以区别必要条件的原因和充足条件的原因，这是逻辑上最重要的区别。
定义13: 一个事件或属性A是另一事件或属性B的充足条件，当且仅当任何时候A发生或出现，B就发生或出现。
定义14: 一个事件或属性C是另一事件或属性D的必要条件，当且仅当任何时候D发生或出现时，C就发生或出现。从这两个定义，可以引出以下几个重要原则:
1)如果A是B的充足条件，那么B是A的必要条件。
2)如果C是D的必要条件，那么D是C的充足条件。
3)如果A是B的充足条件，那么～B是～A的充足条件。
4)如果C是D的必要条件，那么～D是～C的必要条件。
5)如果A是B的充足条件，那么，～A是～B的必要条件。
6)如果C是D的必要条件，那么～C是～D的充足条件。
当我们用日常语言来谈论一个结果的原因时，我们有时意指一个充足条件。例如，我们说传染是患病的原因或者说被压路机碾压是一个人死亡的原因时就是这样。有时我们意指一个必要条件，例如，当我们说有氧气存在是燃烧的原因或者说勤奋学习是得高分的原因时，我们的意思就是指必要条件。另一方面，充足且必要条件有时却根本不是原因，而是症候或征兆。例如，蜡烛的点燃是有氧气的征兆，发高烧是感染的症状。当我们分析穆勒方法时将会见到: 必要条件和充足条件的准确语言较之原因和结果，征兆和症状的含混语言要有用得多。
试图把因果推理的原则加以系统化的第一个人是英国哲学家约翰·穆勒(1806—1873年)。他提出五种实验研究的方法: 契合法、差异法、同异合用法、共变法和剩余法。后来赖德(Georgevon Wright)通过仔细分析，证明穆勒方法既是赘余的又是不完备的。所以说赘余，因为共变法和剩余法没有任何新东西，是不必要的; 所以说不完备，因为他不能识别有时用以探求原因的其他两个方法。下面我们将按照赖特的观点去分析因果推理，把这些实验研究方法看做探寻一个给定事件或属性的必要条件或充足条件的方法。
4．3 直接契合法(Direct Method of Agreement)
直接契合法是辨别一类事件(或一种属性)的必要条件的方法;这个方法的要点是(a)把你相信是哪一类事件的一些可能的必要条件识别出来和(b)把该类的若干事件加以检查，以便确定是否这一类事件始终被已识别出的一个或几个可能必要条件所领先或伴随。如果是这样，并且如果在检查过足够大量的实例后，没有发现任何例外，那么你就有理由(以一定的置信度)作出结论: 这样地辨明的可能必要条件事实上是该类事件的必要条件。
例如一个医学研究者要决定产后忧郁症的原因，显然分娩本身是产后忧郁的一个必要条件，但这不是研究者所要寻找的“原因”。研究者所要知道的是: 什么生理现象在有些分娩而非所有的分娩中出现，但同时却在每个产后忧郁症病例中都出现。如果能够回答这个问题，并且如果这样地辨明的必要条件原来是易控制的，那么产后忧郁就可能治疗，即是说可能通过消除它的必要条件而根绝这种病症。
研究者的第一步是识别出产后忧郁症的一些可能的必要条件。我们假定研究者根据他自己关于同怀孕和分娩相联系的生理变化的知识而提出下面这个理论: 忧郁是由于某种激素的过剩或欠缺所引起的。假定研究者认为有五种激素可能和产后忧郁症有因果关系，于是他开始搜集患这种忧郁症的妇女的数据。在研究了十个病例以后，研究者得到下述结果(“-”表示给定激素的欠缺，“+”表示给定激素的过剩，“Y”表示这个条件出现，“N”表示这个条件不出现):
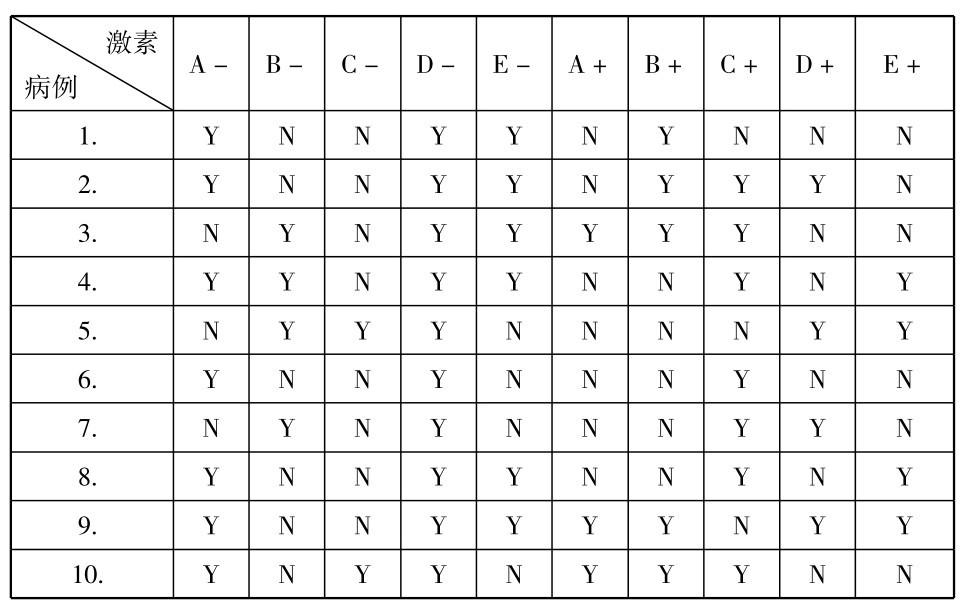
如果研究者所识别的十个选择物之一确是产后忧郁症的“原因”(必要条件)，显然那必定是D-(激素D的欠缺)，因为这是在所有十个病例中都出现的条件。当然我们的研究者无法预先确知所提出的十个选择物中是否有一个确实是产后忧郁症的必要条件，因此，在搜集了十个病例后研究者并不会很确信激素D的欠缺事实上是一个必要条件。如果在一百个病例中没有发现反例，置信度就会增加。置信度将随着没有反例的正面病例数量的增加而继续提高。
如果考虑到所寻找的必要条件也许原来是一个析取，即两个或更多条件中的任一个，原因的寻求就变得更复杂了。例如在关于产后忧郁症的已得数据中，D-并不是唯一的在一切病例中都出现的条件:(A-∨B-)——激素A或激素B的欠缺——也是在十个病例中都出现的。某类疾病的“原因”也许并不只是一个选择物，而是几个选择物之任一，其中没有一个是在一切病例中都出现的。在这种情况下，结果的“必要条件”，是几个不同事件的析取，其中至少有一个是在这类被研究事件每次出现时都被发现是领先或伴随出现的。
直接契合法是寻求一个现象或一类事件的不变的前件或伴随条件的方法。当我们试图辨明不良现象的原因，以便获得阻止它发生的力量时，这是我们通常运用的方法。
4．4 逆向契合法(Inverse Methodof Agreement)
如果我们要消除一种不良的现象，只要辨明那个现象任何易控制的必要条件就够了，因为排除一个必要条件就自然而然地消除掉把该条件作为必要条件的任何现象。但要是我们希望产生一个现象，仅仅辨明那一类现象的必要条件是不够的; 因为仅仅一个必要条件不足以令那个现象发生。要能够随意产生给定的一类现象，我们需要辨明一个易控制的充足条件。逆向契合法就是用于寻求充足条件的方法。
根据上述原则3，如果A是B的充足条件，那么-B是-A的充足条件，因此，为寻找B的充足条件，我们需要寻找任何时候B不出现它便不出现的一个事件。例如，假定某一国家发现一个同全国的变化趋势相反的事实: 某些中学的学生近十年以来在全国性标准测验中的成绩稳定地增长着。要研究的问题是: 为什么会发生这件事? 这个“违反趋势”的现象的原因是什么? 这个例子中所寻求的原因是一个充足条件，一个在这些事例中出现但在测验得分不增加的一切事例中都不出现的条件。研究将采取下述步骤:
(a)搜集有关那些测验得分稳定增加的学校的数据;
(b)辨明这些学校所共有的特征;
(c)搜集有关一些得分并不增加的学校的数据，以便确定是否(b)所辨明的任何特征在后面这些学校中都不出现。
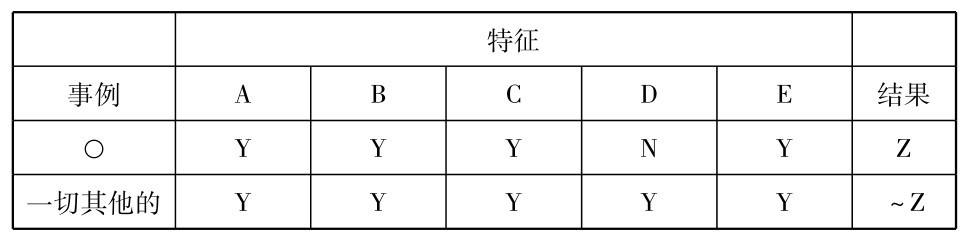
令A、B、C、D、E代表得分增加的一切学校所共有的特征，假定初步的研究结果如下表所示(“Y”表示一个给定特征出现，“N”表示它不出现)。
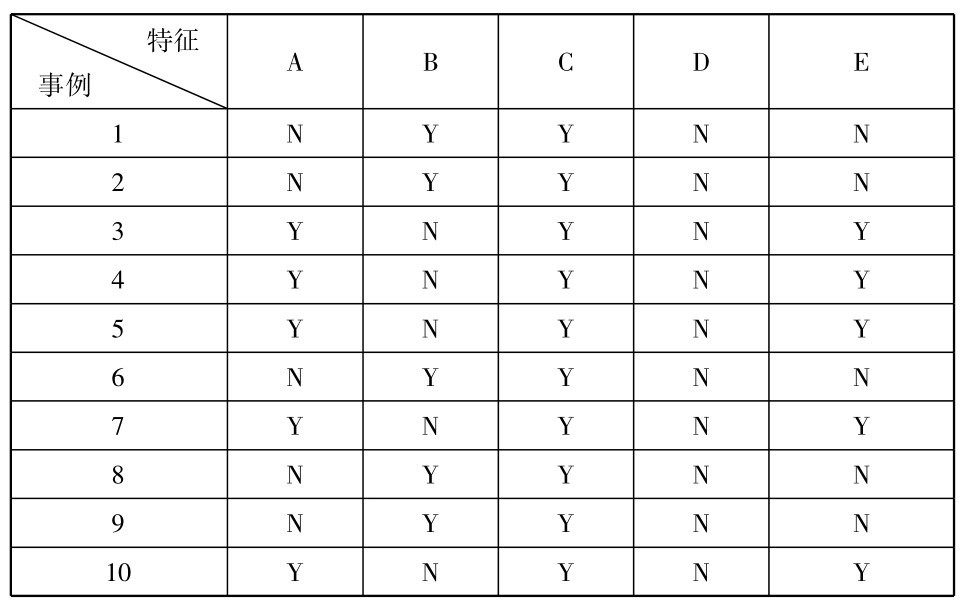
由表中结果人们可以作出结论: 如A，B，C，D，E中有一个是得分增加的充足条件，那么D便是那个充足条件。因为D的不出现一律地伴随着得分的不增加。如果这个假说被更多学校的调查所支持，如果总是发现D的不出现同测验得分的不增加联系在一起，那么人们对这个结论的正确性的置信度就会提高。但在寻求充足条件时，我们一定要考虑到另一种可能性，即不是一个单独事件而是两个或多个事件构成了充足条件。例如，也许是数学必修四年，英语必修四年，基本规则的逐日复习和某些特定教材的使用对于获得成绩的稳定提高都是必须的。如果情况是如此，那么这些条件的仅仅一个的出现将不足以导致所需的结果。例如上表中的论据支持这个假说: ［(A∨B)∧D］就是所要寻求的充足条件。随着越来越多论据的搜集便能够把每个可被选择的假说加以检验。最后，如果我们幸运的话，我们也许能成功地辨明一个充足条件，一个永远为那个理想结果所跟随的条件。
总括地说: 人们为达到使一个理想结果出现的目的一般地寻求它的充足条件，而反向契合法就是寻求充足条件的方法。和直接契合法一样，我们使用这样获得的知识去影响事件进程的能力，要求那些条件是易控制的。如果直接契合所判明的必要条件是不易控制的，那么我们就不能利用关于那个条件的知识来防止把该条件作为必要条件的那个结论的出现。同样地，如果反向契合法所辨明的充足条件是不易控制的，我们关于那个条件的知识将不能使我们获得和该条件始终伴随发生的那个结果。
4．5 双重契合法(The Doublemethod of Agreement)
给定的一类事件可以是另一类事件出现的既必要又充足的条件。就是说事件类型A和B可以具有这样的关系: B类事件永远地被A类事件所领先或伴随(这样便证明A是B的必要条件)，并且A类事件亦永远地被B类事件所跟随或伴随(这便证明A是B的充足条件)。因为直接契合法适用于寻求必要条件，而反向契合法适用于寻求充足条件，要决定给定的一类事件出现的必要充足条件，这两个方法必须合并使用。例如，某地区突然爆发一种新病症，需要知道它的原因。从一些病人抽取血液样品，并且指示出被怀疑为可能病因(必要条件)的几种微生物。这些检验的结果列表如下(Y表示血样中查出给定的一种微生物，N表示没有查出):
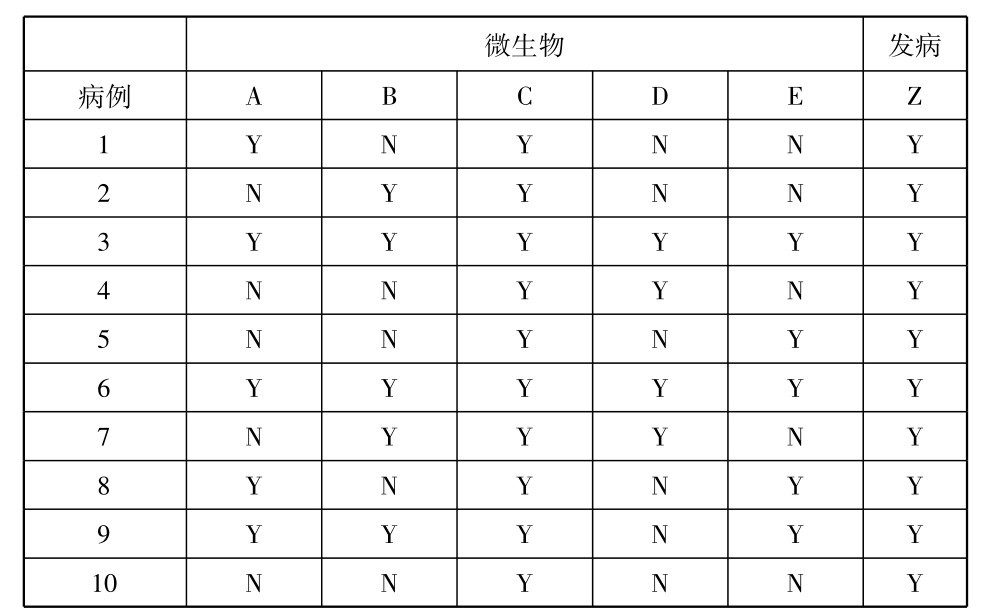
由上列结果，很明显，如果这五种微生物中的一种是该病发生的必要条件，那么微生物C就是那个条件，因为它是在所有十个病例中都出现的。如果有更多的病例确认这个假说，那么对于C事实上是必要条件的置信度就提高了。就可以开始寻找消灭这种微生物以治愈疾病的方法了。
假定有个医学研究者决心培养他希望能够防止这病发生的一种疫苗，而在实验过程中他需要能使志愿者患上这种病。这就提出进一步的问题:已被表明是这病发生的必要条件的微生物C也是一个充足条件吗? 我们的研究者便对几个健康的人(未患该病的人)的血样进行研究，并且发现下列结果:
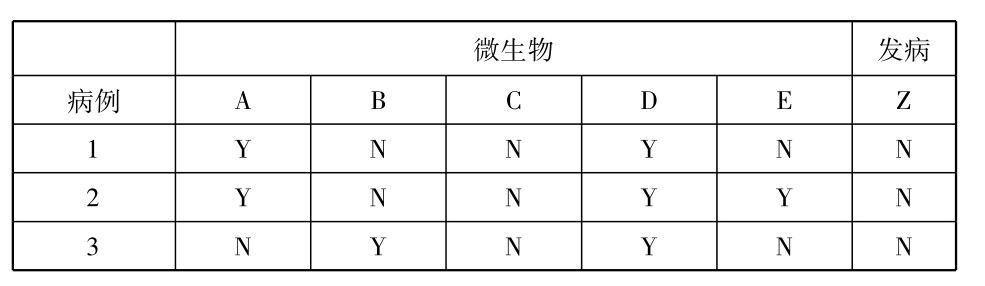
续表
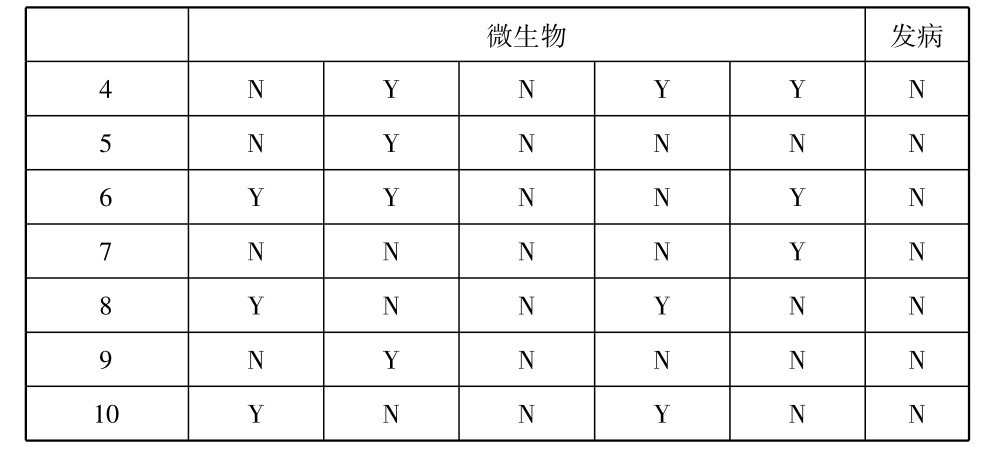
上列结果使人有理由作出下面这个初步结论: 微生物C是该病发作的充足条件，因为在被检查的一切事例中，病不发生都伴随着这种微生物的不出现。如果这个结论被更多的例子所确认，并且如果没有反例出现(即没有出现在健康的被测试者的血样中查出微生物C的事例)，研究者对这个结论正确的置信度就会增加，他就会合理地预料: 给一个健康人的血液注射微生物C就会使那人随即患上该病。
双重契合法是判明一类事件是另一类事件的既必要又充足的条件的方法。它的要点就是把直接契合法和反向契合法相继应用于有关的论据上。如果这样辨明的条件是易控制的，它的辨明就使人具有防止并且导致后一类事件的能力。
4．6 差异法(The Methodof Difference)
如果人们要知道某一类事件的原因，以便获得使那一类事件发生的力量，所需要的所有东西就只是判明这一类事件的任何一个易控制的充足条件。在这种情况下反向契合法便是合适的研究方法。但是，我们有时对判明一个特定事件的唯一原因——例如一次飞机失事的原因或某一座大楼倒塌的原因感兴趣。我们寻求的目标是充足条件，是其出现足以引起事件发生的一个条件。但我们显然不是为了要获得使类似事件发生的能力，而是为了要确定责任所在，或者在某些情况下简单地只是为了满足我们的好奇心。在这样的事例中适用的研究方法叫做差异法。
从理论上说，差异法的步骤好像是人们或多或少随意地搜集关于不倒塌的人行道的特征的数据，然后决定那些特征中的哪一个是在一切不倒塌的人行道中都出现了而在目前例子中却不出现的。实际上，人们当然以颇为不同的方式进行研究。根据相关的工程知识，人们设想出耐久人行道的必要条件一览表: 它们必须是设计成能载重n1磅的，按照这样那样的规格建造的，不可承受大于n2磅的重量，等等。这些是人们以为将要在一切不倒塌的人行道中被体现的条件，其中某一条件的不出现就被推定为被研究的人行道倒塌的原因(充足条件)。
人们研究的结果可以列表概括如下:
那么条件D的不出现便被推定为人行道倒塌的原因(充足条件)。
不要认为差异法仅当人们寻求一个不良或不幸事件的原因时可以应用，当结果合乎意愿时——例如一个原先以为患了不治之症的病人痊愈了——这个方法是同样可用的。在这些事例中，人们也要问: 这个事例和那些其他方面相类似的事例怎样不同呢? 在这个事例中出现而在那些相类似，但结果不相同的事例中却不出现的充足条件是什么呢?
差异法在下面这一点上和反向契合法有别: 反向契合法的目标是辨明给定一类事件的充足条件，而差异法则寻求发现一个在特定时间和地点发生的唯一事件的唯一原因(充足条件)。这个人行道倒塌的原因是什么? 这个病人获得痊愈的原因是什么? 差异法就是寻求解答这种问题的方法。
差异法是在事故调查、医疗诊断、机械故障检修和验尸等领域中使用的研究方法。如果人们寻求说明一个给定家庭中儿童的异常的成绩，某一社区居民的长寿，某一汽车油耗量低或者某一地区涌现的第一流音乐家(或艺术家、科学家)特多的原因，这也是人们要使用的方法。注意在所有这些事例中人们是把被研究事例和相似的但有不同结果的事例加以比较，以便决定(如果可能的话)这个唯一事件的充足条件。
4．7 同异合用法(The Joint Method of Agreementand Difference)
同异合用法像双重契合法一样是辨别一个事件的必要而又充足的条件的方法。它和双重契合法的区别在于寻求其必要充足条件的那个事件是一个特定事件而不是某一类事件的范例。它的要点是: 对有关论据相继地应用差异法和直接契合法。
让我们设想下述情况作为应用这个方法的例子。父母注意到他们的孩子小英比与他同年龄的孩子长得快得多。经过儿科医师的诊断和一系列的检查，并且用差异法确定小英的快速生长率的可能原因(充足条件)是他的过分活跃的脑下腺所分泌的某种激素过多。于是医师用药物使这脑下腺的活动减慢，小英的生长率便恢复正常了。
但这位儿科医师想对这个现象有更多的了解。她要知道异常快速的生长率是否永远为这种激素分泌过剩所领先，即是说，是否这种过剩对于快速生长率既是充足条件，也是必要条件。因此，她参考有关这个问题的许多资料，并且发现在包括男女病人的二十个异常生长率病例中，百分之一百都出现内分泌过剩。因此，她作出结论: 这种激素过剩很可能是小儿加速生长的必要条件。
这样，同异合用法是用来辨明下面这两件事的方法: (a)事件A是事件B的充足条件; (b)A类的一个事件是B类的一个事件的必要条件。
4．8 剩余法(the Methodof Residues)
穆勒认为是一种特殊的实验研究方法的剩余法，事实上不过是差异法的一种变形。由于它是原来的穆勒五法之一，我们将加以简短的讨论。穆勒关于剩余法作了如下的陈述:
由任何现象扣除由以前归纳法已知为某些前件的结果的部分，这个现象的剩余部分就是其余前件的结果。[1]
长期以来，人们爱举的应用这个方法的例子就是导致海王星的发现的研究。按照牛顿理论已计算出已知行星的轨道。人们认为在这些计算的基础上天文学家能够预测任何行星在任何时刻的准确位置。对于除天王星以外的一切行星，这个假定被证明是正确的。但天王星的实际轨道同所计算轨道的差额太大，不能把它归入观察误差。法国天文学家勒费里埃(Leverrier)提出下面这个假说: 天王星轨道的偏差是由在天王星轨道之外的另一个未知行星的引力所导致的。勒费里埃建议天文学家在他的计算所提示的一个确定位置上去寻找这个新行星。过了不久，这个行星(后来命名为海王星)便几乎准确地在勒费里埃所指定的位置上被发现。
穆勒会喜欢这个例子，因为他在提出剩余法时心里所想的显然就是这一类事例。天王星的大部分轨道能够根据太阳和太阳系内行星引力的总和计算出来; 剩下来待说明的——“剩余”——需要另一个原因。因此，如果你把天王星的整个轨道看作其原因有待判明的现象，那么的确好像需有像剩余法之类方法来指导你的研究。但是，如果你简单地把天王星离开预测轨道的偏差作为有待说明的现象，很明显这个现象的必要与/或充足条件可用上文所讨论的各种方法来研究。所以，剩余法并不是判明必要与充足条件的一种不同的新方法。一个复杂现象的必要与/或充足条件必须用适合于这些条件的辨明的那些方法来研究，剩余法不过是用来辨别这个现象的某一部分的方法。
4．9 共变法(The Method of Concomitant Variation)
像剩余法一样，其变法仅仅作为原来的穆勒五法之一而具有主要是历史的兴趣，它并不为前面讨论的方法之外的任何推理辩护。穆勒关于这个方法的陈述如下:
任何时候当现象以任何方式随另一现象以某一特定方式变化而变化，这一现象就是那个现象的原因或结果，或者同那个现象通过某一因果关联的事实而发生联系。[2]
穆勒自己喜欢的应用这个方法的例子就是那个关于海洋潮汐与月亮引力之间关系的推理。穆勒指出我们既不能够把月亮移开以便确定是否这样做便把潮汐也一起消除了，我们也不能够证明月亮的出现是伴随潮汐的唯一现象。穆勒这样推论: 我们能够证明的就是潮汐随月亮的变化而变化。正是这种“共变”证明了潮汐作用“通过某一因果关联的事实”同月亮每隔二十四小时五十分围绕地球一周的表观公转“相联系”。
然而，经过仔细的考虑就可以弄清楚，人们要推论月亮和潮汐之间的因果联系，并不需要这种所谓新的方法。在大到足够展示可测量的潮汐作用的水域，涨潮每经二十四小时又五十分钟出现两次。反复观察便很明显: 每次涨潮都有下述二事件之一出现: 或者月亮在离涨潮出现的地方最近的位置上(把这个事件叫做C)，或者它在离那地方最远的位置上(把这个事件叫做F)。很清楚，在这个例子中我们能够用直接契合法得出下面的结论: (C∨F)是涨潮出现的必要条件。对“共变”可以观察的任何例子都能够给予同样的分析。
4．10 对这些方法的评价
穆勒似乎相信要严格遵循他的五法，就能导致一切可知的因果联系的发现以及已知的因果联系的证明。的确他似乎相信，他提出这五个方法就为归纳逻辑完成了类似于亚里士多德由于提出三段论有效性规则而为演绎逻辑所完成的一切。他的这个想法当然是错误的。他的实验研究方法如上所述不仅是不完备的和赘余的，而且即使有了上面的修正，这些方法也决不能够像穆勒所希望和预期的那样成为研究的普遍工具。
所有这些方法本质上是把可能的必要或充足条件消除掉，直至(如果幸运的话)只剩下一个条件的各种方法。消除的基本原则不外这两个: 如果A能够出现而B不随之而出现，那么A不是B的充足条件; 如果B能够出现而A并不领先或伴随出现，那么A不是B的必要条件。因此，要成功地应用其中任何一个方法，我们必须首先列出可能的必要或充足条件一览表，假设被寻求的那个条件也在其中。然而，这些方法对于列出一览表并不提供指导。回想一下，发现疟疾原因的方法好像简单得很: 一张可能前件的一览表被检验一番，用双重契合法便发现当且仅当病人被某种蚊虫咬过，他们才患疟疾。但如何能够预先知道这个表上包括有“被某种蚊虫咬过”这一项呢? 回答是不能够的。正如我们现在并不知道怎样列出各种癌症或自然流产或无数其他疾病的详尽的可能原因一览表一样。在实际寻求原因时，我们根据关于该现象的一般知识去构造我们的可能原因一览表。例如我们认定癌症可能由生理系统机能失灵，或病毒，或化学剂等等所引起，并且认定它不是由北极平均气温的变化或非洲羊群的增加或无数其他事件所引起。如果我幸而在表上列出了真实原因——真实的必要条件或充足条件，这些方法便能够指导我们去辨明那个原因。如果不是这样，对于如何判别进一步的可能原因，这些方法并不提供任何帮助。
即使我们根据自己关于现象的一般知识构造了一个合理的可能的必要或充足条件一览表，即使由于仔细地应用了合适的方法，我们已辨明那一类现象发生的必要或充足条件(或兼而有之)，我们决不能够绝对地确信我们的结论是正确的，我们也许观察到一千个事例，其中每个A型事件都一律地伴随有一个B型事件。以这些观察为根据我们可以确信地作出结论: A是B的充足条件。可是在第一千零一个事例中我们却发现一个A型事件的出现并没有B型事件相随。原因——必要和充足条件的发现比穆勒所设想的要复杂和不可靠得多。
穆勒方法还有一个缺点: 它们忽视理论的作用。而在对原因的任何合理的寻求中这些理论显然是非常重要的。关于海王星发现的例子就充分显示理论的重要性: 给定伽利略的运动理论和牛顿的引力理论，便一定会有影响天王星轨道的另一颗行星。在这个例子里，并非由于反复观察到天王星轨道扰动和海王星一起出现，从而导致海王星“引起”扰动的结论; 倒是天王星的实际运转状态同所预测的运转状态的显明对照导致另一颗行星的发现。如果理论是正确的，这另一颗行星便必定影响天王星绕太阳运转的轨道。的确，恰恰是在科学理论的基础上我们才辨明那些最终也许被表明是原因(我们所寻求的必要或充足条件)的候补者。若不是由一定的理论出发，医学研究者将不知道在他们判明病因的努力中究竟该去寻求病菌还是该去寻找不吉利的星宿或巫婆的魔法。
因此，上述的实验研究方法并不是穆勒认为他已找到的发现原因的可靠指南。在因果推理中正如在一切归纳推理中一样，没有任何正确无误的指南。但实验研究方法却能够提高我们所得到的结论的概率。对于扮演这个较谦卑的角色，它们是有用的。
4．11 概率和因果推理
同因果推理有关的首先是我们在辨明一个现象的可能原因时所根据的背景知识(包括从各种途径得来的信念)，这可以总称为假设。概率论告诉我们这些假设的概率小于一，即是说，它们是不定的。我们的假设在多大程度上可被怀疑，在这个基础上辨明的可能原因也就在同一程度上可以被怀疑。
其次，作为我们推理的出发点的这些假设即令是可靠的，是否适足以说明被研究的给定现象，也是不定的。例如，细菌病原论就并不说明一切疾病的原因，它只说明由微生物引起的那些疾病。概率论并不能告诉我们所用假设和我们所研究的事例相干的概率多大，它只能告诉我们这个概率小于一。在这一点上发生错误是可能的，这就是为什么一张仔细地列出的可能原因一览表也许并不包括我们所要寻找的原因的第二个理由。
再次，对原因的寻求也许由于测量或观察的错误而走入歧途。在对作为该现象的某个必要条件或充足条件的证据的数据进行分析时，我们必须估计到数据错误的可能性。我们可以通过保持严格的研究程序而降低这种错误的概率，但不能够完全消除错误。任何观察报告或数据完全准确的概率总是小于一。
最后不管我们已观察过多少例子，而且都发现一个A类事件被一个B类事件跟随，因而作出结论: A也许是B的充足条件; 但永远还可能有这样的情况: 仅当和某些我们所忽略的其他相关条件共同出现时，A才是B的充足条件; 若那些条件不出现，A将不会被B跟随。我们的结论的概率将随我们所观察的事例的数量等等的不同而不同，但那个概率决不能达到一。
所以，具有“A是B的必要条件(或充足条件)”这个形式的任何陈述的概率都是下列四个成分概率的乘积:
①我们据以辨别可能的必要或充足条件的背景知识的概率。
②这些背景知识同所研究的现象相关的概率。
③我们的数据或论据免于错误的概率。
④并没有对已被观察的规律性构成未被观察的例外的概率。
显然这些关键的每一方面的概率越高，结论的概率就越高; 每一点的概率都是十分之九，我们的结论的概率便达到约三分之二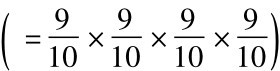
。每一点的概率都是一百分之九十九，我们的结论便有二十五分之二十四(96%)的概率。因此，我们寻求原因时，光应用合适的实验研究方法还是不够的，同样重要的是我们应尽可能做到对下列各点有把握: 背景知识是真的和相关的，论据是准确的，所观察事例是有代表性的。
[1] 穆勒: 《逻辑系统》，伦敦1930年版(该书初版于1843年)。
[2] 《逻辑系统》。