贝叶斯解释
贝叶斯观点把概率演算看作是关于置信度或同置信度相关联的赌博行为的合理性规则或一贯性条件的集合。置信度是贝叶斯解释的基本概念: 概率陈述代表个人的置信度(这是“主观主义的”这个形容词的由来)。但这个置信度与其说是活着的个人的实际的置信度,毋宁说是那些实际置信度的理想化形式,被称为合理的置信度。“合理的”即遵守概率演算的规则的。实际的置信度有时必须这样地修改,以便它们之间的关系满足概率演算的条件。例如某人可能最初对陈述S有等于四分之一的置信度,对非S也有等于四分之一的置信度。但遵守概率演算的规则5,要求他这样地修改他的置信度,以便他对S和对非S的置信度的总和等于1。这样,按照贝叶斯的观点看来,可以说,普通演绎逻辑是完全信念的逻辑,而概率演算则是普通逻辑的扩大,是部分信念的逻辑。让我们解释一下“部分信念”或“置信度”这个概念。
现在如果我准备掷一枚硬币,我可以考虑“它将正面朝上”这个陈述。我相信这个陈述吗? 我想合理的方式是避免或者用“是”或者用“否”来回答这个问题,而可以这样说,“我相信它到一定程度”或者“我部分地相信它”。我们能够根据直觉来规定部分信念的标准,这正是凯恩斯和库普曼(Bernard S.Koopman)所做的。他们都认为部分信念代表能够内省地察觉的概率关系,但并没有测度它们的客观的公共的方法。蓝姆赛指出: 即使有这种内省的测度,也不足以使概率演算成为使人们达到意见一致和在情况不明时作出决策的工具。我们需要某种方法,以便决定一个人的信念什么时候符合我们所规定的条件,什么时候不符合。
蓝姆赛建议根据人们的赌博行为来给置信度下定义。他提出了一种测度部分信念的客观方法。这是最早的贝叶斯解释。
让我们首先把一个道德上中立的命题定义为这样一个其真或假没有关系的命题——就是说,一切其他事情(对我们有影响的一切事情)都相同时,我们并不在乎这个命题是真的还是假的。(例如,“我头上头发的数目是奇数”确实是一个道德上中立的命题。)我们把对一个道德上中立命题的二分之一的置信度定义如下: 假定一个人对于α和β这两个状况并不是不在乎的,就是说,他喜欢α所代表的情况胜过β所代表的情况,或者喜欢β所代表的情况胜过α所代表的情况。再假定他对于(1)“如果命题ρ则α并且如果命题非ρ则β”和(2)“如果命题ρ则β并且如果命题非ρ则α”两者之间无所偏爱,那么他对ρ的置信度便是二分之一。
现在给定一个以二分之一置信度被置信的道德上中立的命题,我们只需要一个任意的出发点: 比方说,“如果ρ则α,如果非ρ则β”这整个情况的值。设这场赌博的值是二分之一。现在我们只需要找到一个恰恰和这场赌博一样地合意的情况γ: 它的值也一定是二分之一。设想这样一场赌博: “如果ρ则γ并且如果非ρ则β”(这里与其α宁愿β); 它的值是四分之三。而赌博“如果ρ则α并且如果非ρ则γ”的值将是四分之一。如果有比β还更令人喜欢或者比α更可厌恶的情况,我们可以把标度展延以便把这些情况也包括在内。重要的只是: 单单这个以二分之一置信度被置信的道德上中立的命题ρ的存在,就足以决定可能情况的值的整个标度。
我们现在能够用全部情况的这些值来决定对任何命题的置信度,包括那些并非道德上中立的命题。如果对一个人来说,有把握地选择α和选择“如果S则β并且如果非S则γ”具有相同的值,那么他对S的置信度便是α和γ的值之差对β和γ的值之差的比率: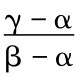 。
。
在这个基础上便可能证明概率论的通常公理对置信度是有效的。蓝姆赛证明下述几个“关于概然信念的基本规律”:
(1)对p的置信度加对非p的置信度等于1。
(2)对p给定Q的置信度加对非p给定Q的置信度等于1。
(3)对p和Q的置信度等于对p的置信度乘以对Q给定p的置信度。(https://www.daowen.com)
(4)对p和Q的置信度加对p和非Q的置信度等于对p的置信度。[1]
他写道:
这些便是概率的定律,我们已证明它们对于置信度的任何一贯的集合是必然真的。违反它们的任何确定的置信度集合就在这个意义上是不一贯的: 它违反了任选项之间的偏好的规律,有如偏好性是一个传递的非对称的关系,并且如果α比β较合人意, β便决不能比如果ρ则α、如果非ρ则β较合人意。如果任何人的心理状态违反这些规律,他的选择便取决于这些任选项被提供于他的确切形式,这是荒谬的。一个狡猾的赌博者会利用赌注记录作弄他,以致使他在任何情况下都输。[2]
莱维把这个正式命名为“荷兰赌定理”(Dutch Book theorem)。
蓝姆赛接着指出: 对部分信念的性质的确切说明,揭示概率定律是关于一贯性的定律,是把形式逻辑扩延到部分信念的结果。它们的作用仅仅是把那些遵守它们的信念集合作为一贯性的辨别出来。“它们的意义并不依赖于对一个命题的任何置信度被独特地决定为合理的”,[3]这就是贝叶斯解释同逻辑解释的根本区别所在。因此,按照贝叶斯解释,没有任何信念集合比任何其他的信念集合是更合理的,只要它们两者都满足概率基本定律所表达的数量关系。
贝叶斯解释的这个不尽如人意的结果,由于另一位赞成主观主义的著名统计学家德·芬内蒂的工作而部分地得到克服。德·芬内蒂提出他称之为“等值的”或“可交换的”(exchangeable)事件的定理。可交换事件的一个序列就是这样的序列: 在序列的事件的一个有限集中,一个给定属性的任何特殊分布的概率仅仅决定于具有那个属性的那一分布中事件的数目。描述可交换事件序列的特征的一种容易方法,是简单地说它们是一些其事件的排序指数不被认为相干的序列。现在举例说明: 设想一颗不规则的骰子。它被投掷落地的方式之一可以是一点向上。让我们把这一类事件称为成功。现在设想这颗骰子的任何一次投掷。这次特定投掷将获得成功的绝对的、无条件的先验概率可以是你所需要的任何东西,按照你由这颗骰子的特殊形状和你的触觉所作出的判断而定; 但是你如果把序列中的各次投掷看作可交换的,像我们大多数人所想的那样,你一定要给第一次投掷、第七次投掷、第三百次投掷、一般地第i次投掷得到成功,都赋予相同的先验概率。这并不意味着,你被禁止从经验中学习; 的确,恰恰是为了允许并且说明从经验中学习,德·芬内蒂才引进可交换性概念以代替传统的独立和等概率(equiprobability)。第n次投掷成功的条件概率(给定关于以前n-1次投掷结果的知识),一般地不同于第n次投掷成功的先验概率。这个条件概率将一般地反映过去事件的频率。
有了可交换事件的序列,主观主义者对“归纳问题”的解决,便使用德·芬内蒂为这些序列所证明的各个不同的大数定律。这些定理的一个突出推断如下: 如果两个人同意一定序列的事件是可交换的,那么,不管他们在开始时抱有什么意见,给定这个序列的一个足够长的部分作为证据,关于未来成功的概率他们将终于达到对一致性的任意接近,只要他们每人都不是这样地顽固不化,以致他的概率评价完全不受频率所提供的证据的影响。这就是说,在他们两人都观察过n次被研究事件的序列后,他们将给第(n+1)次事件的成功赋予顶多相差∈的概率。然而,确实,不管∈定得多么小,总有一个n将使这个陈述是真的。
有两个可避免这个自然结果的反常方式: 其一是否认这些事件是可交换的; 其二是否认过去观察对现在概率分配的影响。蓝姆赛及其后继者所发展的公理都不能排除这些计策的任何一个。现在主观主义观点的支持者好像感到这不过是逻辑的事实。这就是逻辑所能够做的一切,不必多说了。逻辑不能够决定我们的意见,即使相对于汇集的证据; 它只能够规定某些陈述的结合是不相容的(演绎逻辑),或者某些信念的结合是不一贯的(荷兰赌定理)。
逻辑解释的代表像卡尔纳普的典型答复,就是主张有比概率演算的标准公理所表达的那些标准更多的逻辑恰当性(logicaladequacy)的标准。这些逻辑主义者对主观主义者提供概率论基本公设健全性的证明的方法是欢迎的。但他们不认为这些公设是足够的。例如卡尔纳普愿意包括在他的系统内的公理不仅反映和可交换性相应的对称性,而且也反映关于谓词的对称性。他们试图作出精心的改进和发展。
