统计假说和统计推理
1.1 什么是统计推理
统计的、相关的(correlational)和因果的假说都要涉及个体的总体(populations)。辩护这种假说的最重要方法之一就是检查这个总体的若干分子(一个样本),并且由在样本中观察到的结果推论出关于整个总体的结论。任何时候当我们由关于样本的构成的知识作出关于总体的构成的结论,我们就是进行了统计推理。这样,统计推理便可以简单地定义为由样本到总体的推理。
1.2 统计推理的类别
试考虑一下科学家是怎样对统计假说进行辩护的。大致有三种不同的,但相关的辩护方法。他们有时仅仅要对一个总体中的百分比进行估计(estimate),而所根据的又仅仅只是当前对那个总体的样本所获得的知识; 这样的推理叫做估计(estimation)。在另外的情况下,他们要使用他们关于那个样本所知道的东西来检验(test)关于总体的统计假说。这样的推理便叫做“统计假说的检验”。以上两种方法都是经典数理统计所研究和讨论的,又叫做经典推理(classical inferences)。第三种方法便是贝叶斯推理(Bayesianinference)。这种新的统计推理在估计一个总体中的百分比时,不仅要根据当前对那个总体的样本所观察到的结果,还要根据推理者过去有关的经验或知识。这就是说,对贝叶斯推理来说,不仅在当前试验中由反复出现的情况所获得的样本数据是相干的,在试验之前已经积累起来的模糊的或明确的知识也是相干的。特别为了把主观的先验知识(subjective priorinformation)和样本数据结合起来而设计的统计方法就是贝叶斯统计推理。简言之,统计推理可大致分为三类: 估计,假说检验和贝叶斯推理。(https://www.daowen.com)
1.3 简单统计假说
我们在报章上经常看到的关于各种百分比的报道就是简单的统计假说。下面例子是由美国的报纸杂志上取来的:
百分之三十七的美国成年男子吸烟。
百分之二十八的美国成年妇女吸烟。
少于五分之一的美国家庭是其中丈夫为唯一赚钱者的“典型”美国家庭。
几乎一半的所有成年妇女都有工作。
在美国百分之八十的杀人致死都是使用枪支的。
上述陈述都具有相同的基本结构。可以用一个标准的方式来解释它们,就是说,它们都辨认出一个总体,总体的每一分子都具有或不具有一个属性和一个百分比。所以这些陈述的每一个都能够表达为具有下述结构的陈述:
(总体)的x%是(属性)。
百分比告诉你总体中显示该属性的分子的比例。这就是简单统计假说的基本结构。
首先,必须注意“总体”一词并不总是按照字面指一群人。例如上表中最后一个陈述谈到美国的杀人的总体。杀人不是人,而是涉及杀人者和被害者的意外事件。同样地“家庭”也不是人,而是小的人群,但我们能够表述关于美国家庭的“总体”的统计假说。
其次,当你看到一个统计假说时,特别要注意怎样显示总体和属性的特征的方式,留心记下所包括的和所排除的是什么。例如“其中丈夫是唯一赚钱者”这个规定便把其中母亲只做部分时间工作的家庭排除在外了。
1.4 统计分布
谈分布要使用“变项”和“变项的值”这两个有关概念。
任何以不同的类型或数量出现的东西都是一个变项。和一个变项相联系的不同类型或数量就是它的可能的值。例如,在讨论孟德尔遗传学时,我们可以把眼睛颜色看作一个变项,它有两个可能的值,棕色和蓝色。同样地,豌豆的高度可看作有矮和高两个可能的值的变项。另一方面,人的身长则典型地用有许多不同的值的变项来表示,依你怎样地细分等级而定。例如,如果你以英寸为最小单位,从一英尺到九英尺的长度,就使“人的身长”这个变项具有九十六(8×12)个不同的可能值,每个人都仅仅和一个值相符。
可以把任何简单统计假说里所谈到的属性看作一个有二值的变项,例如吸烟者和不吸烟者。但一旦看作一个变项,它就可以有任何数的值。就美国妇女的总体来说,可把“吸烟量”看作所关心的变项。吸烟量的标准度量是每天消费的纸烟的平均数。1980年美国公共卫生局医务主任关于吸烟和健康的年度报告题为《妇女吸烟对健康的影响》。报告里所包含的许多统计量有关于1976年美国成年妇女吸烟者的总体的吸烟量这一变项的分布。这本报告的资料给这个变项仅仅赋予三个值: 少于十五支,十五支和二十五支之间,和超过二十五支;它们的百分比分别是百分之三十六,百分之四十四和百分之二十。注意,这些百分比相加起来是百分之百,这是一切统计分布的一般特点。
很清楚,一个分布便是简单统计假说的合取。但它不是统计假说的任意合取。它是一个包括关于所关心变项的每个值的统计假说的合取。这就是为什么分布中的百分比的总和必须是总体的百分之百。变项被这样地下定义,以便总体中的每一分子都显示变项的一个值,而且仅仅一个值。分布把整个总体按照关心变项所指定的方向来划分。
这个分布告诉你: 百分之三十六的妇女每天吸烟少于十五支,并且百分之四十四每天吸烟在十五支和二十五支之间,并且百分之二十每天吸烟超过二十五支。每一个合取肢本身就是一个简单统计假说。这三个统计假说合起来便显示出整个总体的吸烟习惯。
1.5 简单相关
我们都知道有些属性倾向于同其他属性有关。例如人的身长倾向于和体重有联系。要描述这样一种关系,在科学报告里便说: “身长和体重”这两个变项是相关的(correlated)。
成年美国人构成一个单一总体。在这个总体中,性别这个变项有两个可能的值: 男性和女性。“吸烟习惯”也是有两个可能的值的变项: 吸烟者和不吸烟者。在1.3节里我们看到两个简单统计假说如下:
百分之三十七的美国成年男子吸烟。
百分之二十八的美国成年妇女吸烟。
把这两个陈述合拢来便得到下面这个陈述: 在美国成年人的总体中,性别和吸烟习惯是相关的。这个陈述表达一个相关假说。按照这个假说,“性别”和“吸烟习惯”这两个变项不仅相关,而且在两个变项的每对值之间显示出一种特殊关系,就是:
在美国成年人总体中,吸烟者和男性是正相关的(positively correlated)。
这两个变项之所以是正相关,因为男子中吸烟者的百分比较之妇女中间的百分比要大。这同一关系也可以表述为:
在美国成年人总体中,吸烟者和女性是负相关的(negatively correslated)。
这里吸烟者和女性负相关,因为妇女中吸烟者的百分比较之男子中间的百分比要小。
如果男子和妇女吸烟者的百分比恰恰相同,这两个变项的任何值之间就没有(正的或负的)相关。注意,把正或负相关归于变项本身是没有意义的,仅仅变项的值才能够显示这样的关系。仅当这些变项的有些值是相关的,我们才说它们本身是相关的。
现在让我们把这个例子概括化。给正的、负的和零的相关定义如下:
在给定总体中当且仅当B在A中间的百分比大于B在非A中间的百分比,B和A才是正相关。
在给定总体中当且仅当B在A中间的百分比小于B在非A中间的百分比,B和A才是负相关。
在给定总体中当且仅当B在A中间的百分比和B在非A中间的百分比恰恰相同,B和A才是不相关。
这样看来,简单相关不过是两个简单统计假说的合取。但并非任何两个简单统计假说合拢来都表达一个相关假说。例如百分之二十八的美国妇女是吸烟者和百分之七十二的美国妇女是非吸烟者并不构成一个相关假说。这甚至不是逻辑地独立的两个统计假说。
上面并未谈到相关的强度问题。显然有些相关比较其他的相关更强。而且,一个相关越强,它就会越重要或有用。例如在1935年仅仅百分之十八的美国成年妇女是吸烟者,以别于百分之五十三的男子。这样在1935年吸烟和男性的正相关较之今天的要强得多。那么,粗略地说,
B和A之间相关的强度同A是B者的百分比和非A是B者的百分比之间的差额成正比例。
这样,如果这两个百分比是相同的,相关的强度就等于零。
统计推理中一种最常见的错误就是由已知的相关推论出因果关系的存在。例如在小孩中间身体上出现红点和发烧之间显然有正相关,但红点并不引起发烧,发烧也不引起红点: 两者都是由一种麻疹病毒所引起的。
问题不仅在于,试图根据正相关来辩护因果假说是冒风险的; 相关的性质本身就使相关和因果关系不可能是同一回事。要明白这个道理,让我们回过头看吸烟习惯和性别的正相关。
我们可以用一百个男子和一百个妇女的总体来代替美国成年人的总体(要是你愿意,你可以设想每个人代表五十万人)。为了使这个例子更富于戏剧性,让我们使用1935年的数字。那么男子中间将有五十二个吸烟者,妇女中间有十八个吸烟者,这样在男性和吸烟之间有相当强的正相关。
现在让我们倒转来看这个相关。就是说,我们不问吸烟是否和男性正相关,却问男性是否和吸烟正相关。这就意味着我们应当把二百个男女的总体分为吸烟者和不吸烟者,然后计算男子在每一群内的百分比。将有52+18=70(个)吸烟者和48+82=130(个)不吸烟者。吸烟者中将有52/70=74%是男子。非吸烟者中有48/130=37%将是男子。这样,你便能够看到男性和吸烟是正相关的。看这个相关的两种方式如图(1)所示。
虽然我们所谈的只是一个例子,这个结果却是完全普遍的。如果A和B正相关,那么B将和A正相关,反之亦然。意思是说,正相关是对称关系。如果A和B有这个关系,那么B和A也必然有这个关系。现在不管因果关系是什么,它确实不是一个对称关系。开快车引起意外,但显然意外并不引起开快车。服毒导致死亡,但死亡确实不导致服毒。一般地说,如果是A导致你是B,并不因而必然得出:是B将导致你是A。所以因果关系和正相关是两种根本不同的关系。因而我们也就明白因果假说必定和断定相关存在的假说有所不同了。
1.6 因果假说
因果假说的一些标准例子如下:
吸食大麻导致嗜好海洛因。
糖精引起膀胱癌。
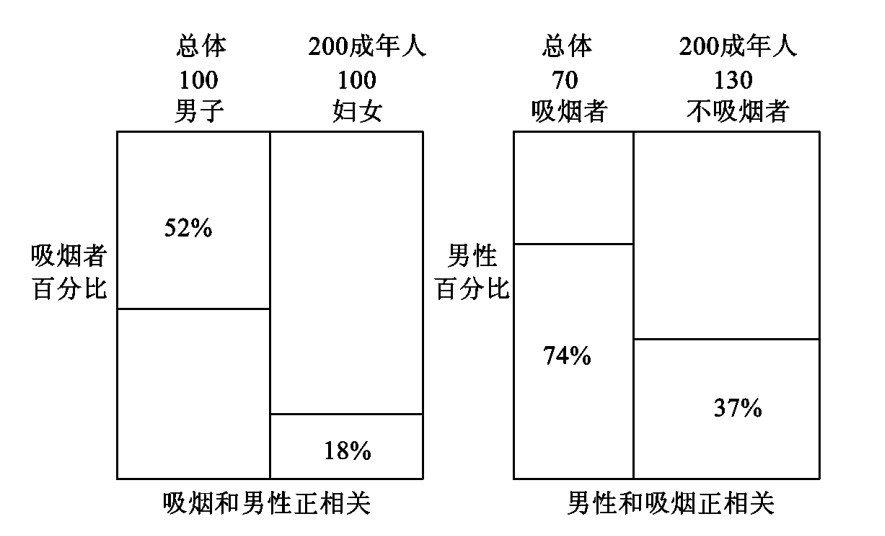
图1
吸烟引起肺癌。
口服避孕药引起致命的血栓。
维生素C增强人对感冒的抵抗力。
首先我们要理解这些假说断定什么,让我们讨论吸烟和肺癌的例子。当公共卫生局的医务主任作出这样的陈述时,它并不是明显地指向某个人的。它也并不主张每个和所有吸烟者都将患肺癌。大家都知道吸烟者中间只有很小的百分比确实患肺癌。那么当断定吸烟引起肺癌时,确切地说,人们所主张的是什么呢?
理解这样的主张的最好方法是把它们看作并不直接谈到个人,却是谈到个人的总体。这是对于总体所作的断定。这里的总体可假定为所有的中国人或者所有的美国人。
要把美国公共卫生局医务主任关于吸烟引起肺癌的陈述理解为谈到一个总体,例如所有美国人。他说在这总体中吸烟是肺癌的一个正因素(positivefactor)。意思是说: 对总体中的有些个人来说,吸烟是导致肺癌的一个确定性因素[1]。对于这些个人,给定他们的内在结构和初始状态,加上吸烟就造成患肺癌与否之间的决定性差别。但总医师和任何人都不知道这些人是谁。假说仅仅说有些人是这样。
我们假定个人是确定性系统。因此如果每个人都同那些吸烟引起肺癌的人恰恰一样,那么吸烟的确会使每个人都患肺癌。但我们知道事实并非如此,所以假定个人是确定性系统,我们必须作出结论; 并非总体中所有的人都恰恰一样。确实大多数人都不像那些吸烟导致肺癌的个人。
如果我们假定个人是随机系统,我们对总医务主任那个陈述的理解也没有改变多少。从这个假定出发,我们将把那个陈述作这样的解释: 对于总体中的有些个人,吸烟是导致肺癌的随机的正因素。
检验简单因果假说的标准实验方法必须把几组不同的个人加以比较,试考虑一个真实总体——例如1980年1月1日的美国成年人。这个总体约有一亿分子。总体中大约三分之一的个人是吸烟者。很容易设想总体中每一个人都吸烟。也很容易设想其唯一差别就是没有一个人吸烟的相同的总体。虽然这两个总体都是纯假设的,我们能够以各种不同方式把它们加以比较,特别是我们能够查问每个假设总体中结果患肺癌者的病发数。
假定吸烟引起肺癌这个假说是真的,按照决定论模型,在每个人都吸烟的假设总体中,有些人(不管他们是谁)就要患肺癌,而在没有一个人吸烟的假设总体中,同样的这些人就不会患肺癌。这样在这两个想象的总体之间就有明显的差别,第一个比第二个会有较大的肺癌病发数。
这个简单的比较模型可以应用于任何的因(C)果(E)关系。其中每个人都被设想为有所谈原因的那个假设总体可用X来表示; 其中每个人都被设想为没有这个原因的假说总体用K来表示。在每个假设的总体中,都会有若干个人得到那个结果。这些分子分别地被称为*EX和*EK。但使用百分数比使用实在数目总是较好。很容易由实在数目求出百分比。
由关于真实总体的陈述开始,我们现在已经把那个陈述扩充为关于两个纯假设总体中相对的肺癌病发数的陈述。每个假设总体除去各自的不同特征(X或K)外都恰恰同真实总体相似。现在我们就可以为提供表达简单因果假说的更好方式的三个相关概念下定义了。
当且仅当%EX大于%EK,在真实总体中C才是E的正因素。
当且仅当%EX小于%EK,在真实总体中C才是E的负因素。
当且仅当%EX等于%EK,在真实总体中C和E才是因果上不相干的。
这样,现在我们并不简单地说: 吸烟引起肺癌。我们改说: 在美国成年人的总体中,吸烟是引起肺癌的正因素。
上述因果假说显示出因果假说的一般形式。注意按照这个模型,一个因果假说包括三个成分。它谈到一个因素(例如吸烟),一个结果(例如肺癌),和一个总体(例如美国成年人)。
如果我们要说某一事物防止另一事物,最好使用负因素的概念。这样,“服维生素C预防感冒”这个假说就可以这样准确地表述: “服维生素C是在所有人(或所有中国人,等等)的总体中患感冒的负因素。”用因素代替原因,暗示对于相同结果可能有其他的因素,包括正的和负的。
上述分析假定了个体的确定性模型。要是我们假定个体是随机的,只需要作较小的修改。主要的区别是这样: 假定总体中有些个人患肺癌的概率由于吸烟而增高,并不逻辑地蕴涵着下述陈述: 如果每个人都吸烟比起如果没有一个人吸烟来,确定地会有较多的病发数。我们能够说的一切便是: 很可能会有较多的病发数。这样,在X中肺癌患者的“平均”数或“期望”数会大于在K中的这些相应的数。下一节将告诉我们这些概念是什么意思。
为了作出决策,知道什么事物是一个因素往往不如知道它是多么大的一个因素那么重要。例如在医疗中,知道某一疗法对于多少人可能有帮助比单纯地知道会帮助有些人更重要。在医疗中,我们用有效性这个名词来谈这个问题。我们要知道把某一疗法应用于一个给定总体会有多大效力。让我们把这个概念推广,用“有效性”一词来谈任何因素,不管是好的还是坏的。
对一个因素的有效性可以有各种不同的度量。最简单的度量便是%EX和%EK之间的差额,不过是用小数而不是用百分比来表达的。令Ef(C,E)表示在给定总体中C产生E的有效性,简单的公式如下:
Ef(C,E) =*EX/N-*EK/N
因此我们的有效性度量的范围可以从-1到1,零度便相应于因果上不相干。要切记这个定义并不适用于个体,但却适用于总体。一个给定因素可以对一个总体很有效,而对另一个却完全无效。
你一定会注意到我们关于正相关的定义和正因素的定义是平行的。同样地,相关强度的定义和因素有效性的定义也是平行的。但因果关系和相关并不一样,你现在便能够看得更清楚了。
相关是存在于某一实在总体中的两个属性之间的一种关系。例如性别和吸烟的相关是由现存的美国成年人的真实总体中在男子中间和在妇女中间的吸烟者的相对数来下定义的。简言之,一个相关是由谈到真实总体的两个统计假说的合取来下定义的。
另一方面,因素却是由真实总体的两种假想的形式来下定义的。例如,说吸烟是患肺癌的正因素并不是单纯地说: 在现存总体中事实上吸烟者中间比较不吸烟者中间有更多的肺癌患者。这仅仅是相关。而是说: 在其他一切情况照旧的条件下,如果每个人都吸烟较之如果没有一个人吸烟,就会有(就可能有)更多的肺癌患者。这是一个很不相同的陈述。简言之,一个因果关系是由谈到两个假想总体的统计假说的合取来下定义的。
