统计假说的检验
4.1 检验假说(the test hypothesis)
由样本到总体的一切归纳推理在原则上都能够按照区间估计的方法来作。但是经典数理统计已经发展出建立于检验统计假说这个概念基础上的一个相关的方法论。这个方法论被广泛使用于生物学、心理学和社会科学中,而且这些科学的成果的报告常常使用这种检验方法论的语言。许多的这些报告是具有重要的实际意义的,要理解这些报告,你必须懂得作为其基础的方法论。此外,因果假说的辩护也是大部分以检验方法为根据的。
在对所有层次的所有各种歧视进行讨论时,统计推理占据显著地位。我们现在用一个假想的歧视例子。美国大学录取学生不是通过考试的,而是根据对申请人的一切情况的审查决定的。美国某州立大学(简称ESU)被控在研究生的录取上对女性歧视。由于有关歧视的规定,ESU没有关于申请攻读研究生的男性和女性相对录取比例的记录。但是他们倒知道对所有申请者的全部录取比率。因此,他们知道任何申请者的录取概率P(A)。他们要面对的问题是妇女的录取概率P(W)是否和P(A)不同。如果这些比率是相同的,歧视的指责就没有什么根据了。那么,争论焦点的假说是P(W) =P(A)。这个叫做检验假说。它就是要用由一个合适总体的样本得来的统计数据来加以检验的假说。
从逻辑观点看来,关于一个检验假说最重要的一点就是: 它等值于一个简单统计假说。它断定一个特定总体的分子的一个独特的百分比具有某一个指定的属性,例如,被ESU的研究生院所录取的属性。即使要检查单单一年的记录(由于申请者和被录取者的巨大数量)也需要很长时间和大量的耗费,所以,研究生院决定用关于妇女申请者的一个随机样本来检验这个假说。假定他们开始用一百人的样本,再假定全部录取比率是百分之五十。这个假定只是为了便于计算,它并不重要。我们即使给P(A)假设任何其他的值,例如零点四或零点二五,基本方法完全一样。
研究者检查他们的样本以便决定在随机地选出的一百名妇女申请者中间录取的相对频率。检验统计假说的方法论的任务是用这个观察到的频率来判断检验假说P(W)等于零点五的真或假。
这种研究的一个可能结果是否决这个检验假说,就是作出结论说: 它是假的。我们看看这样的结论是如何可以得到辩护的。
让我们简单地称检验假说为H,在ESU研究中,H便是P(W) =0.50。让我们考虑一下如果H是真的,我们能够预期什么事情要发生。
我们所知道的关于这种研究的最重要事情,是由这样一个总体随机地选出的一百人样本的抽样分布,这个总体的半数个体具有被ESU的研究生院所录取这个属性。这个分布,由图7来表示。图7是由第二节关于抽样分布的图添加一些有关材料而制成的。主要的增加是把离开平均值两个标准差以内的可能的样本频率的集合称作在零点五水平上非统计地显著的,或非SS(0.05)。其涵意是: 那些不在平均值的两个标准差之内的可能的样本频率便叫做在零点五水平上统计地显著的,或SS(0.5)。
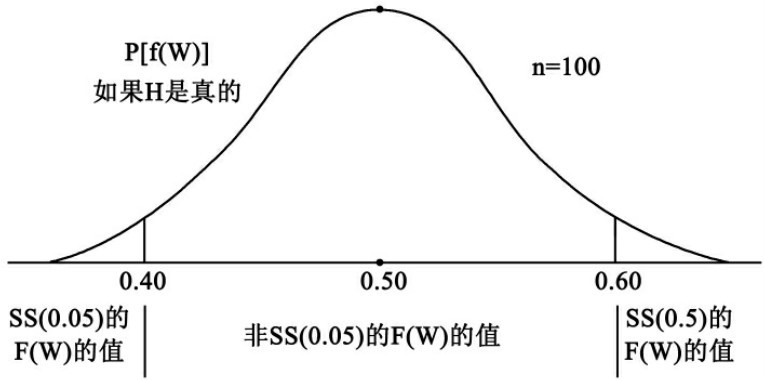
图7 表示样本量一百的在统计上显著的频率的抽样分布
“在零点零五水平上统计地显著的”,意思就是: 所观察到的频率离开当H是真的时我们的期望值在两个标准差以上。
你也许已经猜到: SS(0.05)中的“0.05”来源于这个事实: 在零点零五水平上的一切统计地显著的频率的总和概率是零点零五。这是由于另一事实; 在平均值两个标准差之内的一切频率的总和概率是百分之九十五,这些频率根据定义是非统计地显著的。有时候科学家使用零点零一的显著性水平,只有那些距离平均值三个标准差以上的可能的频率才是SS(0.01)。按照在社会科学中的一般习惯,我们将用零点零五做我们的标准。如果你看到不标明水平的SS,可假定是零点零五。
关于统计地显著的频率的唯一普遍重要的事情,就是它们在辩护统计假说中的作用。这种作用的一部分简要地表述为这个归纳的规则:
否决检验假说的规则: 如果被观察到的样本频率是统计地显著的,便否决这个检验假说。
“否决这个检验假说”的表述是检验方法论的标准用语的一部分。根据我们的措辞,它的意思就是: “作出检验假说是假的这个结论。”
回到ESU研究上来,假定发现一百个妇女的样本只有三十八人被录取,这样f(W) =0.38。f(W)是一个统计地显著的频率。只有在零点四和零点六之间的频率才是在平均值的两个标准差以内。一个被观察到的频率零点三八在这个区间之外,因而是在零点零五水平上统计地显著的。运用否决检验假说的规则,研究者应当作出结论。H是假的。一个女性申请者被录取的概率不是零点五。
当然,H是假的并不由已知事实演绎地得出来,H是真的,并且随机地选出的一个一百人的样本显示出仅仅三十八人被录取,是逻辑地可能的。但这个结论是归纳地得到辩护的。使用这个规则而得到一个假结论的概率只有百分之五。如果H确实是真的,我们观察到一个统计地显著的频率,因而错误地作出结论: H是假的,这件事的概率只有百分之五。我们知道概率只是百分之五,因为我们晓得了抽样分布。
那么,P(W)的值是什么呢? 答案是由区间估计方法给出的。由一百人的样本的相对频率零点三八,我们作出结论: 真的概率是在零点二八和零点四八之间,用一个只有一百人的样本,我们不能够合理地作出和这个不同的任何其他结论。
不幸,统计检验的报告通常并不包括所观察到的实际频率。一个典型报告会仅仅给出差别的方向(较高的或较低的),以及是否这个差别是统计地显著的。例如,研究者向ESU董事会提出的报告也许仅仅说,所观察到的录取妇女的频率低于全部的比率,并且其较低的分量是统计地显著的,但并不指明显著性水平。假定零点零五水平,那只告诉我们f(W)在零点四以下。由这个数据我们能够合理地作出结论: P(W)是小于零点五。但这是我们所能够说的一切。
如果报告只说差别是统计地显著的,甚至略而不提差别的方向,我们就只能够作出结论: 妇女录取比率不等于零点五。那就容许妇女的比率大于零点五的可能性。
现在让我们假定另一个可能的结果: 一百名妇女申请者的样本得出四十二人被录取,给定了检验假说,f(W)等于零点四二是非统计地显著的。我们怎么办呢? 我们肯定不能够做的一件事,是接受检验假说为真的。这个假说断定: 妇女录取的总比率恰恰是百分之五十。我们由区间估计的研究懂得: 并没有任何这样的简单统计假说能够被合理地接受。
由于不可能辩护这个检验假说本身,有些统计学教科书便建议简单地作出这个结论: 检验未能否决检验假说。这个结论显然是合理的,因为由检验的描述和所观察结果是非统计地显著的这个事实,这个结论可演绎地得出来。但还有一个提供更多知识的可以归纳地得到辩护的结论。
我们能够做的一件事是构造适当的区间估计。当一个统计检验不能够否决检验假说时,这样做总是合理的。在目前这个例子中,对一百人的样本应用我们的经验估算法便得出结论: P(W)是在零点三二和零点五二之间。这个区间当然包括H为真的可能性在内。
但要构造适当的区间估计,你必须知道被观察的频率,这在我们的例子中是零点四二。通常没有报道这个频率,人家告诉你的一切便是: 被观察的频率是“非统计地显著的”。不幸,这远远不如告知实际的频率提供那么多的知识。知道一个一百人的样本对一个零点五的检验假说未能得出统计上显著的结果,不过告诉你所观察到的频率是在零点四和零点六之间。但甚至这样不足够的知识我们仍然能够在归纳上很好地加以利用。
如果被观察频率f(W)是零点四,我们能够合理地(用区间估计)作出结论: 总比率P(W)是在零点三和零点五之间。同样地,如果f(W)是零点六,我们能够合理地作出结论: P(W)是在零点五和零点七之间。并不知道实际的被观察频率是在零点四和零点六之间的何处,我们便只能够作出结论: 总比率是在零点三和零点七之间的某处,这个结论是为区间估计方法所辩护的。
妇女录取比率在零点三和零点七之间这个结论所提供的知识并不多。但是,给定所观察频率是“非统计地显著的”这个相对地不提供知识的报告,这是我们能够得到的最好的结论了。标准的检验方法论的不幸的特点之一就是: 它鼓励这样的报告。既然我们大多数人都无能力改变这种习惯,我们能够采取的最上策就是对它的缺点有所防备。
让我们把P(W)居于零点三和零点七之间这个假说称为DH,意思是扩散的检验假说(diffusetesthypothesis)。DH包括这个检验假说和其他假说的系列。能够容易地提出这个范围宽广的假说便使我们得以陈述下列相当简单的归纳规则:
不否决检验假说的规则: 如果给予了被观察频率,便构造合适的区间估计; 如果不给予被观察频率,那么作出结论: DH是真的。
你知道怎样使用区间估计方法去决定什么比率包括于DH中。我们已经晓得使用区间估计得到一个真结论的概率是百分之九十五。所以,上述规则是一个好的归纳规则。不管P(W)的实在值是什么,使用这个规则给你一个得到真结论的至少百分之九十五的概率。
4.2 样本量和统计显著性
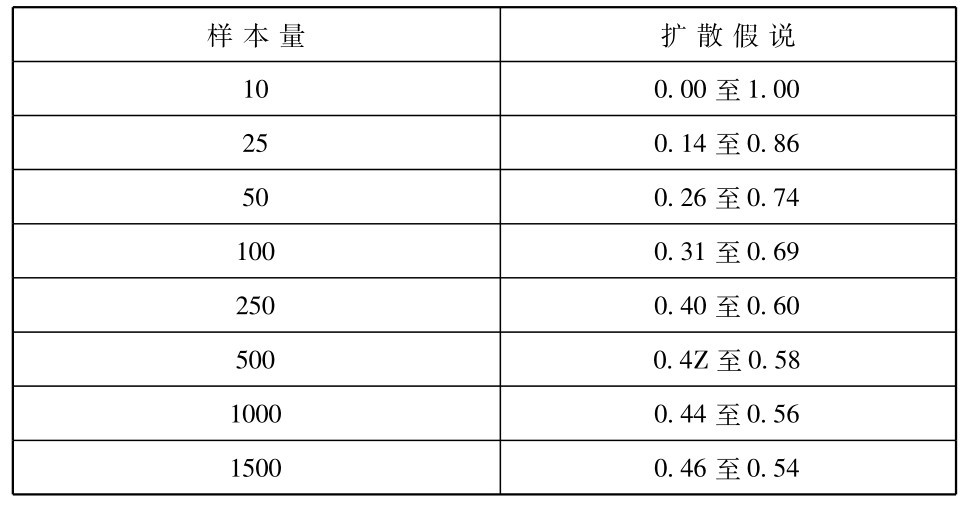
你已经知道区间估计的误差边际随样本大小而变化。样本越大,误差边际便越小。因为扩散的检验假说DH是用区间估计来构造的,这个道理对它也适用。样本越大,包含DH的区间便越窄。假定H所断定的比率是五十比五十,有些具代表性的值便被陈列于表2中。
在样本量和统计显著性之间有相对应的关系。样本越大,当作统计地显著的被观察频率和期望频率之间的差别便越小(请记取: 期望频率就是在H真时抽样分布的期望平均值)。
这种关系在我们的ESU研究生申请人的例子中得到很清楚的说明。对一百人的样本来说,百分之三十八便是一个统计地显著的数。但是,如果这样本只包括五十个妇女,百分之三十八(或者五十人中的十九人)将不是统计地显著的。像你从表2所看到的,对于五十人的样本,少于百分之三十六(五十中的十八)就会得出统计地显著的结果。
同样地,对于我们的一百人的样本,百分之四十二不是统计地显著的。但一个二百五十人样本的百分之四十二(或一百零五人)便会是统计地显著的[请检查表1]。但是百分之四十四(或二百五十中的一百一十),便不是统计地显著的。
这一点告诉你: 不提及样本量的关于“统计显著性”的报告是没有意义的。被观察频率和检验假说所预测的平均值之间的任何差别都可以是或都可以不是统计地显著的。一切都决定于样本的大小。这样你如果读到一份断言或者“统计显著性”或者“非统计显著性”的报告,但你不能够说出这个样本所包括的究竟是二十五,二百五十,还是二千五百个对象,那就不要管它。这个报告是毫无价值的。
表2 对各个不同的样本量和一个零点五的被观察频率来说的、同一个扩散检验假说相对应的近似的区间
上文对检验方法论的解说假定一个零点零五的显著性水平。就是说,我们以距离检验假说所预测的平均值的两个标准差作为统计显著性的边界。现在你应当能够正确了解显著性水平的改变会怎么样。因为实际上研究者所报告的偏差至少是平均值的两个标准差,我们只需要考虑如果把显著性水平降低到,比方说零点零一,将发生什么情况。
零点零一的显著性水平意味着小于平均值的三个标准差的差别都是在零点零一水平上非统计地显著的。这样,在我们的ESU的研究生申请人的例子中,一百人中仅仅三十八人录取还不是在零点零一水平上统计地显著的。这好像我们已经为使ESU研究生院避免受性别歧视的指控找到一个便宜的途径。简单地把显著性水平定在零点零一上,相应地把一个区间估计的置信水平定为百分之九十九,这样以一百之中的三十八这个观察值为根据的置信区间包括零点五作为P(W)的一个可能的值。难道较低的显著性水平(和较高的置信水平),不是永远较好吗?
你应当怀疑这样一种推理。如果它是正确的,那么任何观察频率不管距离平均值多么远,都可以被宣布为“非统计地显著的”,你只需要把显著性水平定得足够低。但没有一个有声望的科学家会这么做。理由在于: 较低的显著性水平(或较高的置信水平)不必定是较好的。较低的显著性水平意味着: 如果假说H事实上是真的,我们错误作出H假的结论的概率较低。相应地,较高的置信水平意味着把真值包括在置信区间内的概率较高。但这些利益也有它们的代价。代价是得到一个包含的知识太少以致一点也不重要的结论的概率增加了。
假定使用零点零一的置信水平,ESU研究生院的报告指出: 一百个女性申请人中只有三十八人录取,并无显著性的差。即使他们报告了实在频率是零点三八,有百分之九十九的置信水平的置信区间将跨越从零点二六到零点五的一切比率。如果他们并不报告实在频率,相应的DH便会甚至更为宽广。这些区间包括并无歧视的可能性,但它们也包括可以显示出严厉歧视的可能性。简言之,在查验过一百个案例以后,我们终于得到这一个结论: 也许有也许没有歧视。但在观察一个单—案例之前我们就已明白这一点了。
降低显著性水平以便作出结论: 观察结果是“非统计地显著的”,被证明是得不偿失的。但是,在要求承认统计显著性时,报告较低的显著性水平却可以是提供信息的和有用的。例如,如果一百个女性申请人被发现只有二十五个录取者,这可以被报告为在零点零零零一水平上统计地显著的。这份报告也许说: “结果是高度地统计上显著的(P<0.0001)。”即使它们并不报告实在频率零点二五,但已至少告诉你它大大超过如果H真时所期望平均值的三个标准差。这就比起单纯地说它是SS(0.05)(即在零点零五水平上统计地显著的)能提供更多信息,当然那样说也是真的。
一般地说,你阅读用检验方法论语言来草拟的统计研究报告的目的是要发现被给定资料所辩护的最有内容的(提供最多知识的)结论。要做到这一点你也许必须利用关于样本量、显著性水平等等你所知道的一切。你的努力的酬报是知道你已从报告中得到尽可能多的东西。即使这个结果被证明小于你原来所预想的,至少你会由于晓得自己所作结论并未超过合理限度而感到安慰。
图8可提供统计假说的检验方法的一般图解。你可以给上面讨论过的例子填进有关细节。所研究的总体是什么? 待检验的假说是什么? 样本多大? 观察频率是什么? 它是否统计地显著的? 等等。
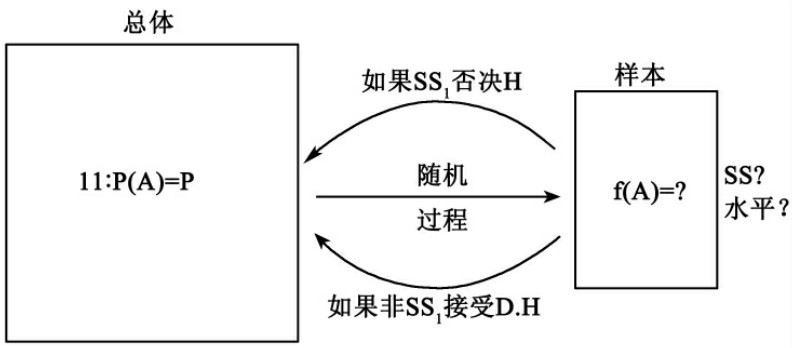
图8 统计假说H的检验的图解
4.3 统计检验和统计推理
我们现在可以把检验方法论中的推理过程揭示出来,把这些检验中所体现的推理以有明显陈述出的前提和结论的推理形式表达出来。让我们先看看前提,然后看相应的推理形式。
我们将仅仅考虑这样的例子: 其中统计研究的结果即观察频率仅仅作为或者是“统计地显著的”,或者是“非统计地显著的”被报导出来。如果给定了观察频率,适当的反应便是构造一个区间估计,而我们已经晓得了和那个方法相联系的推理形式(参看上文3.2节)。这样,合适的推理的第二个前提将包括“SS(0.05)”这个陈述或者“非SS(0.05)”这个陈述。还需要什么其他的前提呢?
由任何统计假说以及一个样本量n已从合适的总体随机地被选出来这个事实能够演绎出一个抽样分布,这一事实就会提供一个可能的前提。让我们把n对象的随机选出叫做统计检验的初始条件IC。这样,对任何的样本量来说,下述推理的一般形式是演绎地正确的:
H(假说)和IC(初始条件)
所以,以概率等于百分之九十五,观察频率f将不是SS (0.05)。
既然这个推理是正确的,下述条件陈述就必定是一个重言式:
如果(H并且IC),那么,以概率等于百分之九十五,f不是SS(0.05)。
我们将把这个条件陈述称为统计假说H的检验的条件1。条件1是一个重言式,并不需要辩护。
提供第二个可能前提的关系显示于图9中。这个图形显示出三个不同的统计假说的抽样分布。一个是检验假说H。这个假说决定哪些频率是统计地显著的。其他两个假说,H-和H+,相应于组成一个扩散假说DH的值的区间的两个端点。这个扩散假说,由于技术上的理由,与前面谈到的扩散假说不同。但在大多数实际用途上这个区别是不重要的,这是使用同一缩略词的理由。
在这里,DH的端点是用下述方法来选取的。H对应于选出有一个指定属性A的个体的概率P(A)。要找到H-,考虑小于H值的P(A)的值。对于这些值的每一个来说,得到一个统计地显著的结果的概率大于零点零五。你只要观察到更多的分布是在标出SS(0.05)的区域上就能够理解这一点了。随着我们考虑P(A)的越来越小的值,最终我们将找到这样一个值,为它得到一个统计地显著的结果的概率是合适地高,比方说百分之九十五。P(A)的这个值和H-对应。对P(A)的更小的值,一个显著结果的概率大于百分之九十五。注意对P(A)等于零,这个概率便是一。一个相似的推理过程导致和假说H+对应的P(A)的一个值。
用一百的样本和一个断定P(A)等于零点五的检验假说,DH包括P(A)从零点三一到零点六九的一切值。你用一个计算器和一套好的概率表能够把这个算出来。但使用我们粗略的关于区间估计的经验推算法,我们也得到一个从零点三到零点七的区间。对我们的目的这就足够近似了。
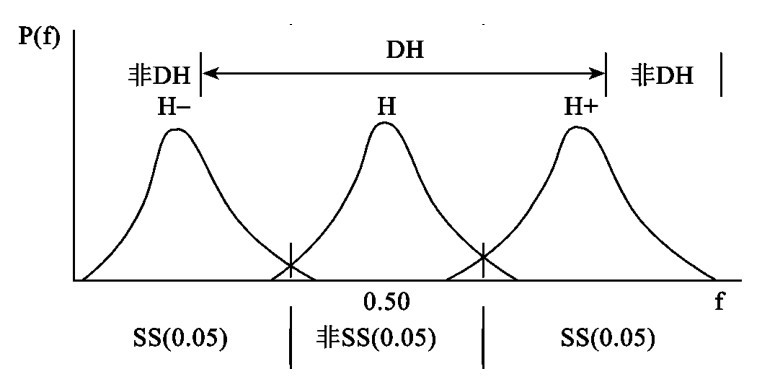
图9 检验假说H和扩散假说DH的抽样分布
给定DH被决定的方式,下述推理是演绎地正确的:
并非DH和IC;
所以,以概率大于百分之九十五,f将是SS(0.05)。
注意,这个推理的前提包括扩散假说的否定。非DH包括一切不包含在DH中的总体比率的可能的值。对于一个一百样本和断定两半等分的H,这些就是在零和零点三一以及零点六九和一百之间的一切可能的比率。
上述推理的正确性当然保证下面这个概率陈述是真的:
如果(非DH并且IC),那么,以大于百分之九十五的概率,f将是SS(0.05)。这个陈述将被叫做假说H的检验的条件2。
任何时候用随机抽样来检验一个统计假说,条件1和条件2两者都将得到满足。因此,它们两者都可用作辩护统计结论的推理的前提。
由于我们设置统计假说检验的方式,观察样本只能够产生两个可能的结果之一: 或者观察频率是统计地显著的,或者不是。让我们首先考虑它是统计地显著的。在这个情况中,我们便像下面这样地推理:
第一前提 如果(H并且IC),那么以概率等于百分之九十五, f将不是SS(0.05)
第二前提 f是SS(0.05)
预备结论 并非(H并且IC)
预备结论 并非H或者并非IC
增添前提 IC
最后结论 非H
由最初两个前提到第一个预备结论的步骤是归纳的。如果前提都是真的,结论也为真的概率是百分之九十五。其余的步骤都是演绎地正确的。增添的前提断定样本是随机地被选出的,这是辩护最后结论所需要的。结论是H假。
这个推理形式可以缩成两个前提和一个结论。这个推理的“短式”是:
如果(H并且IC),那么以概率等于百分之九十五,f将不是SS(0.05)。
f是SS(0.05)并且IC。
所以(归纳地),非H。
你可以把这个看作用以反驳一个检验假说的推理的标准形式。
像上文指出的,你将不仅被告知: 观察频率是统计地显著的,而且也被告知: 它是大于还是小于如果H真时所期望的频率。在这个场合你能够有理由不仅作出H假的结论,而且作出总体中的实在比率在H所指定的比率之上或之下的结论。
如果观察频率不是统计地显著的,我们便使用条件2来推理如下:
如果(非DH并且IC),那么,以概率大于百分之九十五,
f将是SS(0.05),
f不是SS(0.05)并且IC,
所以(归纳地),DH。
这个推理的“长式”同反驳检验假说的推理的长式相似。我们将把“短式”作为这种推理的标准形式。它是一个好的归纳推理。特别要注意结论是DH。不可能为H本身辩护。我们能够做到的,顶多便是辩护一个包括H为其组成部分之一的扩散假说。
在任何时候使用随机抽样方法来进行统计检验,两个结论中的一个将得到辩护。结论或者是非H,或者是DH; 不管样本的大小都是如此。但是,得到这些结论中的这一个或那一个的概率,关键取决于样本的大小。样本越大,当作统计地显著的可能样本频率的数便越大。而且扩散假说DH的内容决定于样本的大小。样本越大,DH所包括的总体比率的差距便越窄。样本量的这两个特点是藏在检验方法论后面的“逻辑”的充分表现。
4.4 相关假说的检验
检验方法论不仅用于简单统计假说,而且更常用于相关假说的检验。
令H是关于学生用大麻和尝试海洛因之间有相关的假说。但H不是一个简单因果假说,它仅仅断定两个变项之间的相关强度不是零,这包括许许多多的可能性。然而H的否定却能够归约为一个简单统计假说。
在其最简单的形式中,H的否定断定在那些用大麻和不用大麻的学生中间,尝试海洛因学生的百分比没有任何差别。在检验方法论中“无差别”的主张叫做虚假说,简写作H0。
曾尝试海洛因的大麻吸用者的百分比可以用条件概率P(T/M)来表示。这是一个随机地选出的大麻吸用者曾尝试海洛因的概率。同样地,在不吸用大麻的那些人中间尝试海洛因者的百分比是P(T/非M)。这两个数之间的差就是相关强度,我们将简写作SC(T,M)。H0可以看作一个简单统计假说,因为它断定一个单一的总体参数SC(T,M)有唯一的值即零。
虚假说当然是由观察那些用大麻和那些不用大麻的对象中间曾尝试海洛因者的相对频率来检验的。让我们分别以f(T/M)和f(T/非M)来表示这些频率。这两个频率之间的差叫做d。SC(T,M) =0这个虚假说将由观察d的值来检验。
d的观察值和虚假说之间的关系类似于一个统计假说H和一个相对频率f之间的关系。H0和随机抽样的初始条件一起蕴涵着观察的频率差的可能值的一个抽样分布。这个分布的形状和个别频率的抽样分布一样。但是它的期望值永远是零。就是说,如果总体中没有差分,样本中的差的最概然的值也是零。
在平均值的两个标准差以内的d值不是统计地显著的差——在零点零五水平上。这样,如果H0是真的,观察到一个统计地显著的差SSD(0.05)的概率只是百分之五。相应地,观察差并非SSD(0.05)的概率便是百分之九十五。
否决一个虚假说的规则类似于否决一个简单统计假说的规则。
否决一个虚假说的规则: 如果观察差d是统计地显著的,否决H0。
遵守这个规则会导致否决一个真的虚假说的概率只是百分之五。
因为H0是H的否定,否决H0便等值于接受H,如果你有理由否决H0,你就有理由作出有相关的结论。但其对于这相关的强度如何,却什么也没有说,那是另一个问题。
反之,如果观察差被报导为非统计地显著的,我们能够作出什么结论呢? 我们当然不能作出H0真的结论,那是没有好理由的。我们倒要作出结论: 一个扩散的虚假说DH0是真的。DH0包括H0,但也包括SC(T,M)的其他不同于零的值。因为我们被给予实在的频率,我们能够猜测每一个范畴内的对象的数,以便估计相关的强度。任何这样的估计当然都包括零作为一个可能性。如果我们并不晓得频率,只被告知观察差是“非统计地显著的”,我们对DH0的大小的猜测将必定包括可能的相关强度的较大范围。
那么,合适的规则是:
不否决虚假说的规则: 如果观察频率被给定,估计相关的强度。如果观察频率不被给定,作出DH0真的结论。
这个规则导致一个假结论的概率小于百分之五。这样,就那个用大麻的例子来说,我们作下述结论是稳妥的: 或者并没有相关,或者在尝试海洛因和偶尔吸用大麻之间只有很弱的正相关。
你辩护关于相关的结论所用推理和辩护关于简单统计假说的结论所用推理具有恰恰相同的形式。检验假说H0的两个条件是:
1. 如果(H0并且IC),那么以概率等于百分之九十五,并无SSD(0.05)。
2. 如果(非H0并且IC),那么以概率大于百分之九十五,有一个SSD(0.05),
所报导的观察的频率差被假定为或者是统计地显著的,或者是非统计地显著的。
如果所报导的差是统计地显著的,你在下述形式的推理中使用条件1:
如果(H0并且IC),那么以概率=95%,
并无SSD(0.05)。
SSD(0.05)。
SSD(0.05)并且IC。
所以(归纳地),非H0(或者,H)。
如果报导的差分是非统计地显著的,你在下述形式的推理中用条件2:
如果(非DH0并且IC),那么以概率大于95%,
有一个SSD(0.05)。
并无SSD(0.05)并且IC。
所以(归纳地),DH0。
4.5 统计的显著性和实质的重要性
一个统计研究的结果只需是离开当假说真时的期望值两个标准差,就成为统计地显著的。究竟观察频率离期望值必需多么远才合格地是统计地显著的,关键决定于样本的大小。用小的样本,一个在其他情况下大的差也许仍然是“非统计地显著的”。同样地,有大的样本,一个在其他情况下小的差也许是“统计地显著的”。这样,有统计的显著性或者缺乏这个显著性,并不是这种研究的实在重要性的可靠的标志。
在统计检验的结果可能导致错误想法的许多方式中,最严重的是: 由于样本不够大,揭露不出重要的差分而作出并无统计显著性的报导,我们的ESU研究生录取方法便提供一个好例子。
假定一百人的样本已得出一个非统计地显著的结果: 录取人数为四十二。即使知道观察频率,百分之九十五的置信区间包括零点三二和零点五二之间的妇女录取概率。这便包括像零点三三这样的值,那是严重歧视的初步证据。因此,统计的结果虽然是完全合理的,却不能接触到实质问题——他们究竟是否歧视?
原则上,P(W)的小于零点五的任何值都提供歧视的某些证据。但是实践上,有些小于零点五的值不值得继续研究。其他的值则确定地值得研究。哪些值值得继续研究不是一个科学问题,而是一个法律或社会政策问题。那么,让我们假定美国司法部以此作为有关联邦政策问题,已经决定十点之差是值得继续研究的。这就意味着: 实质问题不仅仅是P(W)是否和零点五有差分,而是它是否和零点五相差至少十点。所提出的研究虽然提供一个合理的统计检验,却是设计不适当,不能应付这个实质性问题。
假定P(W)真的是零点四,一个一百人的样本会显示出f(W)的一个统计地显著的值,从而导致否决H的概率是什么呢? 恰恰是百分之五十左右。有P(W)等于零点四的一百人的样本的概率分布跨立于统计显著性和非显著性之间分界线的两边,每一边都有半数的概率分布。这样,即使事实上存在着诉诸法律的根据,这个统计检验仅仅有二分之一的机会导致这个结论。我们也许还是掷一个铜币好,那样会快得多和容易得多(见图10)。
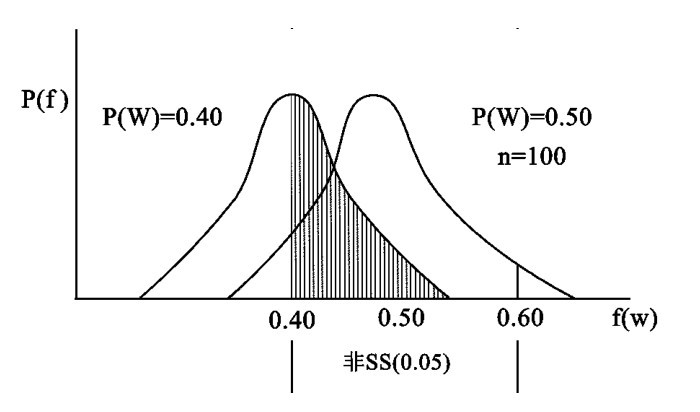
图10 抽样分布显示出根据仅仅一百人的样本进行检验的缺点
那么,原来一百人的样本就是太小,不能够解决这个实质问题。如果P(W)的真值和零点五有重要差分,就需要大约五百人的样本才会有否决H的高概率。这是细心的研究者早该知道的。
一个非专家要决定一种研究的设计是否适宜于应付实质重要性的问题,是困难的。那要求对于该题材有相当多的知识。但是在任何时候你读到宣称“并无显著差分”的结果,你都应当自问一下是否样本足够大。在重要差分真正存在的场合能够得出一个SSD(0.05)。
另一方面,有大样本的研究也可能会发现并无或很少实质重要性的“显著”结果。这不是很严重的问题,因为人们永远能够简单地忽视不相干的信息。但你首先要认识到它是不相干的。例如,美国1970年对大学生的调查发现,在吸烟者和不吸烟者中间尝试海洛因的比率有“显著的”差分。但这个差分只是统计地显著的。它对于是否吸用大麻是尝试海洛因的一个因素的问题是不相干的。这个相关的理由简单地在于: 吸烟是吸用大麻的最普通方式,不吸烟者吸大麻的就较少。而在吸大麻和尝试海洛因之间确有清楚的虽则比较弱的相关。
在任何时侯你遇见一种统计研究声称的“显著性”时,自问一下是否这差分仅仅是统计上的,也许只是有大样本才可发现的,抑或是真正重要的。
4.6 因果假说和随机化实验设计
随机化实验设计提供因果假说的最好检验方法,我们现在以“糖精引起膀胱癌”这个简单因果假说为例,可以把它确切表述如下:
受糖精影响是实验鼠发生膀胱癌的正因素。这个假说断定: 如果所有的鼠都受糖精影响较之如果没有一只鼠受糖精影响,就会发生更多的膀胱癌病例。因为随机地选出一个发病的个体的概率P(E)相等于发病个体在整个总体中的百分比E,我们的因果假说可以这样地表述: P(E)x大于P(E)k。
由于检查整个总体是不大可能的,我们通常安于选取一个样本,然后由样本逆推到总体。但是要给一个假想的总体取样显然是不可能的,更不要说具有不相容的特征的两个假想的总体了。那么我们如何检验因果假说呢?
答案是: 我们创造真的样本来扮演两个假设总体的样本的角色。我们这样做的方法是: 从真实总体中随机地选出一个样本,然后随机地把它分为两组。一个组里的所有分子都这样地受实验操纵以便它们具有为我们叫做x(代表“实验的”)的假设总体下定义的条件。另一组的分子受如此的实验操纵以便它们具有为我们叫做k(代表“控制的”)的假设总体下定义的条件。于是这两个组恰恰像是由两个假设总体取样得到的一般。它们分别地被称为实验组(x组)和控制组(k组)。
在糖精的实验中,研究者从一组实验鼠开始,这些鼠是按照仔细规定的条件被养育的,因此,可以被看做是一切这类鼠的随机样本。我们能够可靠地假定: 把个别的鼠标明为实验的还是控制的是由一个随机过程决定的。x组里的鼠被喂以含有百分之五糖精的食物,而k组的鼠吃同样的食物,但减去糖精。
结果当然每一组里都有一定相对数的鼠发生膀胱癌。我们将把这两个频率分别标作f(E)X和f(E)R。现在我们已把检验一个因果假说的问题归约为同检验一个简单相关问题具有恰恰同样结构的一个简单问题。我们实际上有由两个不同总体取来的样本。虚假说H0是: 膀胱癌的病发数在两个总体中是相同的; 就是说,P(E)X=P(E)K。虚假说和关于从每个总体中有一些个体被随机地抽样的陈述(IC)一起便逻辑地蕴涵f(E)X和f(E)K之间可能的差的概率分布。这个分布的平均值当然是零。
如果H0是真的,两个标准差以内的d的一切值的集便有百分之九十五的概率。这样,根据定义,这些差是在零点零五水平上非统计地显著的。大于两个标准差的差分则是在零点零五水平上统计地显著的。同样地,一定有Ef(C,E)等于P(E)X-P(E)K这个有效性的某一极小值,使得如果糖精是那样地有效的,D的观察值便有百分之九十五的概率是统计地显著的。这里我们应同时考虑糖精作为原因的有效性的正值和负值。在原则上这是可能的: 糖精是实验鼠中发生膀胱癌的一个负因素。也就是说,可能糖精起抑制膀胱癌的作用,因而降低受其影响的总体中膀胱癌的病发数。所以我们应当考虑在正负两个方向上都会有产生一个SSD(0.05)的百分之九十五的概率的极小有效性。Ef(C,E)的这两个值便决定这个扩散虚假说DH0,它断定这个因素的有效性将比以百分之九十五的可靠性揭示出来的为小。
4.7 辩护因果假说
按照美国国会技术评估署(Office of Technology Assessment,简称OTA)1977年对加拿大实验研究的概述,第二代实验鼠产生k组中八十九分之零(或0%)的膀胱癌,和x组中九十四分之十四(或15%)的膀胱癌。这个差分被认为是在零点零零三水平上统计地显著的。因此,合理的反应便是否决H0和接受H。就是说,我们作出这个结论: 从怀孕开始便受糖精影响是实验鼠中发生膀胱癌的因素。而且既然喂糖精的鼠的癌症比率大于控制组的比率,我们便作出结论: 它是一个正因素。
因果假说的辩护也可以用这一已熟知的推理形式表述如下:
如果(H0并且IC),那么以百分之九十五的概率,将没有一个SSD(O.05)。
有一个SSD(0.05)并且IC。
因此(归纳地),并非H0(或者H)。
第一个前提当然是由概率的计算得到辩护的。第二个前提是观察值和实验设计与执行情况的记录。这个因果假说(至少对于鼠)确实有理由是不大能够怀疑的。
加拿大的研究也给我们提供了辩护不成功的好例。实验鼠的第一代只在诞生后才受糖精影响,在x组中产生七十八分之七(或者9%)的癌症。而在x组中七十四分之一(或者1%)的癌症。这个差分是在零点零五水平上非统计地显著的。我们由此作出结论: 一个较宽的扩散虚假说DH0是真的。
辩护这个结论的推理又具有以下熟知的形式:
如果(非DH0并且IC),那么以大于百分之九十五的概率,将有一个SSD(0.05)。
并没有SSD(0.05)并且IC。
因此(归纳地),DH0。
像上述推理一样,这两个前提也是有好理由的。
因为对零点一以下的频率,我们由经验估算法得出的区间大得使人有错误想法,我们便不能够对DH0的大小作出好的估计。我们也不能够利用OTA概述里所报告的实在频率来估计糖精在第一代实验中的有效性。当然我们知道任何这样的估计必定包括零度有效性,因为差分不是统计地显著的。
4.8 有效性和统计显著性
在第4.5节里我们晓得一个“统计地显著的”结果也许显示出或者也许不显示出对于被抽样总体是“重要的”情况。这个教训在这里同样适用。实验组和控制组之间的一个统计地显著的差分也许显示出,或者也许不显示出有关因素的高度有效性。要记住有效性是根据总体中分子要是受或不受该因素影响便产生或不产生这个结果的相对数来下定义的。
总体中的有效性和两个样本之间的一个统计地显著的差分的联系环节是由样本量提供的,如果不指明样本的大小,关于统计显著性或非显著性的任何报导都是毫无价值的。但是即使知道了样本的大小,你也常常不能够作出关于因素的有效性的任何合理的结论。
你能够辩护任何关于有效性的结论的唯一场合是: 如果有大的样本(例如超过一千)而没有SSD,在那个场合“扩散”虚假说将是相当窄的。意思是说: 被估计的有效性是在零度周围的一个狭窄区间内,比方说( -0.05到+0.05)。在一切其他场合,你就不能够说什么。有大的样本,有效性无论大小,都容易产生一个SSD。因此,只知道以大样本而有一个SSD,你还不能够说这个是由于一个大的有效性还是由于小的有效性所致。
以小的样本(比方说,二十五左右),甚至相当高度的有效性都不大会产生一个SSD,一个比较弱小无力的正因素当然几乎没有产生SSD的机会。所以,仅仅知道样本小而没有SSD,你不能够说这有效性究竟是小的还是相当大的。
甚至有了一个SSD,如果样本是小的,有效性的估计将是包括一些相当小的值的宽广区间[例: n=2.5: ME=0.22; f X=0.75; f K=0.30; 所估计的PX=(0.53到0.97); 所估计的PK=(0.08到0.52); 所估计的Ef=(0.01到0.89),因为(0.53-0.52) =0.01并且(0.97-0.08) =0.89]。
当然最理想的情况是你被提供关于一个因素有效性的权威估计。甚至仅仅告诉你实在的样本频率也还是有帮助的。你也许能够根据这些频率作出你自己对有效性的粗略估计。缺乏这样的报导,你就只好依靠下表所概述的经验估算法了:
表3 样本量,有一个SSD和有效性估计之间的关系的概述

