决策的策略
3.1 决策的三个类型
在决策论中,只在很稀少的场合,把不同的可能结果的效用加以比较或度量,就能够决定你应当选择什么行为。在这些场合,你已经知道在你采取行动时什么情况将要发生,所以决策是容易的。你只需选择相对于那个状态会产生有最大效用的结果的那个行为。这是一个通常的决策策略,但重要的一点是: 决定什么是最好的行为,依赖于你所掌握的关于可能状态的知识。
决策策略由于你所掌握的情报的性质不同而一般分为三个类型。你确定地知道哪个状态θ将要发生的场合,是情况确定中的决策; 另一个极端是假定你对于什么状态将要发生毫无所知或所知甚少,这叫做情况不确定中的决策。居间的场合便是知道每一可能状态发生的概率,这一类型的决策需要使用样本数据,叫做带风险(risk)的决策。在第一种场合,决策是简单明确的。把不同行为加以比较的唯一度量是效用函数U(α,θ),我们应当选择将产生有最大效用的结果的那个行为。但这样的场合是不现实的,在这种场合中的决策在实践上是无关紧要的,我们不必加以讨论。
第二个类型即情况不确定中的决策,就是不掌握样本数据,对客观概率完全无知或所知甚少,面对这种情况而进行决策,可以称为不确定的抽彩给奖法。第三个类型有风险的决策也可以称为有风险的抽彩给奖法。这两种决策策略是下文要加以讨论的。
3.2 不确定的抽彩给奖法
在没有样本资料可以依据的情况中,我们也许有关于可能状态θ的某些知识,即决策者关于θ的先验概率分布π(θ)。这个先验分布也许以决策者对于相似情况的过去经验为基础,反映θ的不同的值的相对发生率。也就是说,决策者对于各个可能状态的相对的客观概率有了大致的估计。把这些估计加以考虑,决策问题就类似于第三个类型已掌握客观概率的决策了。另外,先验分布也许表示建立于主观判断和客观证据的某种混合基础上的关于θ的不同值的置信度。最后,也许我们并没有关于θ的任何明确的知识,我们不过选择π(θ)作为这种无知状态的约定表示式。后面这两种情况中的决策是真正不确定的决策问题。
在情况不确定中的决策策略可以根据上一节所谈的效用函数来考虑。如果不采用效用论的结构,也可以根据损失函数L(α,θ)来考虑应当采取什么行为。个别的值L(α,θ)测度在状态θ发生时如果我们采取行为α将会遭受的损失。决策的目的是选择相对于损失函数L(α,θ)的最佳行为。在指定先验分布π(θ)之后,现在根据先验期望损失
∫L(α,θ)π(θ)
来评估我们的可能行为,并且选择那个期望损失极小的行为作为最好的行为,就似乎是明智的。在这种情况中,决策论所提出的选择行为的标准就是使由相对于π(θ)的L(α,θ)的平均值所提供的单一求和度量极小化。
这种选择策略与效用论使期望效用极大化的原则是直接类似的。
一切争论之点都是环绕着应当怎样构造先验分布以及最佳选择决定于所假设的先验分布π(θ)的形式这个问题而产生的。如果不仅不赞成效用论,也不同意先验分布的观念,认为不应当以这种主观概率作为决策的依据,那么在不确定中的决策就好像没有行为选择的任何形式基础了。要是没有关于可能状态的其他形式的知识,就只好采取极小极大(minimax)原则了。
3.3 情况完全不确定中的决策
经典数理统计传统否认主观概率的作用,因而否认先验概率在解决决策问题中是有意义的。他们便把“不确定性”了解作对世界的可能状态完全不确定或毫无所知,决策的唯一基础是决策者所采取的价值母式(valuematrix),即可能结果所具有的价值的级别或度量。这样,如果有最佳行为的话,必须仅仅根据这个价值母式来决定哪个行为是最佳的。现在我们假定人的行为和世界的状态是独立的,看看在完全不确定中怎样解决决策问题。
在对于可能状态无所知时有一个判别较好的(或较坏的)行为的方式,即使价值母式仅仅表示结果的级别而不定量化,也是如此。
例如,设想你已决定购买一架好的照相机,只是还要考虑是现在就买还是明年再买。你所喜欢的照相机都是日本或德国制造的,高档进口商品价格的上涨比工资收入的增加要快得多。你不知道这个通货膨胀率是否继续保持不变。如果继续膨胀,而你推迟一年再买,你便要支付更多的钱去买相同的照相机。当然如果这类商品的涨价水平降到一切其他东西(包括你的收入)的大致相同水平,你现在买还是推迟在金钱上就没有任何差别,假定你的决策单纯根据金钱上的考虑,你的可能行为是“现在买”和“推迟”,有关的可能状态是通货膨胀很快或并不,价值母式如下图所示:

图12 通货膨胀期间购物的价值母式
图12中的价值是这样决定的: 如果你现在买,你便以这个对象现在所具有的价值买到它。我们把现在价格和“这个对象实在的价值”等同起来是方便的。所以你可以认为如果现在就买,你一点损失也没有。你恰恰支付你所得到的东西,这样你既不受损失,也并不获利。给这个行为的结果分配价值零。把以这个数额为基数的收益和损失分别叫做+x或-x。这样上图中第一排第一行的值便是“○”。现在,如果并无通货膨胀,你现在买或以后买都没有关系,你的支出仍旧一样。但如果你推迟,就有所不同了。如果通货膨胀,但你现在买了,你也没有任何损失。你用它所具有的价值得到它。但如果你推迟,并且涨价了,你就损失所涨的金额。你支出更多的钱得到相同的商品。所以第二排第二行的价值是-$x。
如果你考虑图12的母式,你应当能够看到现在买显然是较好的行为。现在买你不会损失,如果以后买,你可能损失。
思考这种现在买“不会损失”的特点的系统方法如下: 要考虑的只有两个可能的状态。如果第一个状态(没有通货膨胀)发生了,那么两个行为都是同等地好的。如果第二个状态(通货膨胀)发生,那么第一个行为较好。但假设两个状态之一必定发生,因此,不管什么状态出现,“现在买”较之“以后买”更好或一样好。你对于哪一状态将要发生也许完全没有把握,这并不要紧。如果你选择现在买,结果不可能比以后买更坏些。
让我们把这个观念表述为一般的定义如下:
就我的两个行为a和b来说,当且仅当至少在一个状态中a有比b价值更高的一个结果,并且没有任何状态使b比a有价值更高的结果,a才是比b较好的行为。
如果a比b较好,我们就说b比a较坏,这个关于较好和较坏行为的定义即使在你的价值母式仅仅评出结果的级别时也是适用的。
3.4 最佳的行为和满意的行为
在通货膨胀例子中,现在买不仅是较好的行为,而且是可能有的最佳行为。当仅仅有两个可能选择时,两者中较好的就自然是最佳的。但一般地说,不管有多少其他选择,一个行为也能够是最佳的,只要它比起一切其他选择都较好就行。让我们把这个作为一个显定义来陈述:
在一个可能的行为集中行为a是最佳行为(Ba),当且仅当它比一切其他行为都较好。
很清楚,如果你的价值母式展现出一个最佳行为,你应当选择它。我们可以把这个简单原则陈述出来,作为不确定中决策的第一规则,最佳行为规则。
不确定中决策的第一规则:如果行为a是价值母式中的最佳行为,选择它。
例如在通货膨胀问题中,你应当现在就买,这是最佳的行为。
这个决策原则表明通常应付通货膨胀的一个方法是行不通的。这就是劝说人们自愿地减少他们的一部分消费: “为了大家的利益。”这样就使大家面临这个决策: 根据其他的人的行为而决定减少消费与否。这个决策的价值母式恰恰和原来例子的相似,只不过现在的两个有关状态是“足够多的他人减少消费”和“没有足够多的他人减少消费”。如果他们减少消费,也许没有通货膨胀,如果他们不这样做,就会通货膨胀。但这还是真的:对每个人来说,“现在买”仍然是最佳的行为。
同样一种推理也适用于西方国家想要涨价的大公司和要求增加工资的工会,现在就提出是最佳的行为。劝导人们“暂缓提出”并不能改变局面。如果决定政策的当权者认真想缓和通货膨胀,他们必须想办法改变个人和其他决策单位的价值母式,比方说,对现在购买的商品加征一项可浮动的购物税。如果你现在要支出的额外税款同以后因通货膨胀而受的损失一样大,现在买就不再那么显然地是最佳行为了。很可能较少的人这样做,因此就会产生较少的需求,价格便不会上涨了。
如果没有最佳的行为可供选择,是否会有“足够好的”行为呢?“足够好”是什么意思呢?
一般的想法大概是: 在任何决策问题中,决策者心目中会有被认为是满意的结果的最低价值。如果有一个行为可以至少保证这个极小值,而没有一个行为可以保证任何较大的值,他便会选择使可满意的极小值得到保证的那个行为。
让我们设法使这个一般观念更准确一点。首先我们要指定会令决策者满意的那个极小价值水平,下述定义可以做到这一点:
对一个给定决策问题的决策者的满意水平就是决策者看作这一决策的满意结果的那个极小数值(或最低级别)。
那么一个满意的行为就可定义如下:
行为a是在一个给定决策问题中满意的行为(Sa),当且仅当与行为a相联系的每一可能结果都有一个和决策者对那个问题的满意水平至少一样大的值。
我们现在就可以定出在完全不确定中决策的第二规则,即Sa规则了。
不确定中决策的第二规则:如果行为a是价值母式中唯一满意的行为,选择它。
举一个例来说明。问题是要决定给你的汽车配置一个三年电池或一个五年电池。用三年的电池价格三十美元,用五年的价格四十美元。假设两种电池都没有担保,所以不管发生什么情况,你都无法脱手。但假定你得到可靠的情报: 五年电池将确实可使用五年,不多也不少。但三年的就比较难以预测。它也许可用三年或四年,无法准确断定。照例假定状态和行为是互相独立的,我们便得到下图中的价值母式。
图13中的母式没有最佳行为,如果三年电池只用三年,你买五年电池较合算。但如果三年电池可用四年,你买三年的较合算,你要理解这一点。即使这个价值母式并不展现出最佳行为,但它表明一个可满意的行为。如果你是买主,并且认为使用电池每年花八元是可接受的,那么你应当买五年电池。那个选择对你说是一个满意行为。买三年电池对你可能较合算,也可能较不合算。买五年电池便保证在任一场合下都有满意的结果。
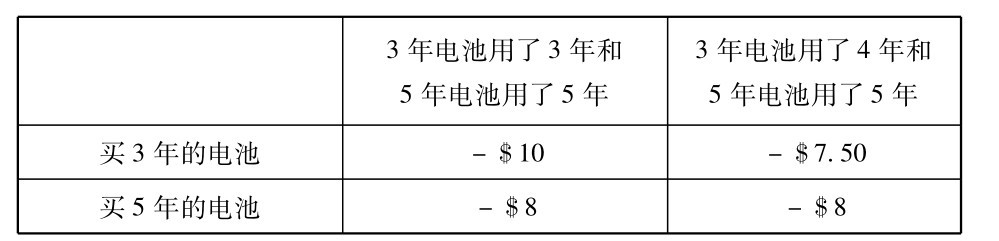
图13 电池问题的价值母式
这个关于满意行为的规则局限于仅仅有一个满意行为的场合。如果满意行为不只一个,你就面临另一个决策问题。应当选择哪一个满意行为呢? 你应当选择提供最佳的“赌博”的那个满意行为。
3.5 赌博的求稳
每个价值母式都至少有一个最高价值的结果。大多数仅仅有一个。让我们暂时假定只有一个。那么把一位赌博者定义为不顾一切风险寻求最好结果的人是很自然的。这就是选择与最高价值的结果相联系的那个行为。如果你这样做,你也许得不到那个结果。但如果你选择其他行为,当然你根本不能够得到那个结果。
把这个观念表述为一个决策规则(赌博者的策略),便是:
不确定中决策的赌博者规则:选择与有最高价值的结果相联系的那个行为。
注意,这个规则适用于当行为和状态是互相独立的,并且仅仅有一个最高价值的结果时的不确定中的决策。
吸烟决策问题提供说明行为中的赌博者规则的一个好例:

图14 简单的吸烟决策的价值级别母式
图14中的级别是根据吸烟对决策者是一种享受的假设而决定的。为了使例子简单化,假定“易受感染”的意思是: 如果你继续吸烟,到五十岁左右必定会有严重后果(比方说患心脏病)。“不易受感染”表示你一定不会因吸烟而患任何疾病。决策者选择的次序是1,2, 3,4; 从价值最低的到价值最高的。显然决策者把吸烟而不受感染看作最称心合意的结果,一个遵循赌博者规则的决策者便会选择继续吸烟而希望不受感染。仅仅有一个最高级别的结果,而吸烟就是可能导致那个结果的唯一行为。
吸烟决策的价值母式显示出一个共同的模式: 有最高价值的结果的那个行为同时也是有最低价值结果的行为。所以如果你赌博输了,你便输光,你得到最坏的可能结果。
如果有同样最高价值的结果不只一个,前后一贯的策略似乎是注意到那些次高价值,并且采取对应于总的最高价值以及最高的次高价值的行为。如果这样的行为不只一个,注意那些第三高的价值中那个最高的,如此等等。这个策略最终将使你取得一个唯一的决策。
已经清楚地说明在决策中“赌博”是什么意思,让我们试图同样清楚地说明怎样才是谨慎地进行决策。一般地说,一个谨慎的人就是比起尝到好结果来更关心于避免坏结果的一个人。一个谨慎的人将放弃可得到很好结果的一个机会而更愿意有得到次好结果的保证,如果导致很好结果的那个行为也可能导致很坏的结果。
我们将要下定义的策略事实上是很谨慎的策略,更像“稳健”而不像单纯的谨慎。在决策的范围中,求稳是根据一个行为的安全水平来下定义的。
任何行为的安全水平就是和那个行为相联系的最低价值的(或最低级别的)结果的数值(或级别)。
非形式地说,一个行为的安全水平就是如果你采取那个行为方案便会得到的最坏结果的值。但这是注意事情的黑暗方面。看到事情的光明方面,如果你选择这个行为,你便可保证得到至少有和安全水平同等价值的一个结果。你不可能得到更差的结果,因为安全水平根据定义就是和那个行为相联系的最低可能的值。
就算晓得最低层在哪里是令人愉快的,人们却永远宁愿这个最低层尽可能地高。这个观念体现在下述不确定中决策的求稳规则中:
不确定中决策的求稳规则:选择那个有最大安全水平的行为。
这个规则在决策论中称为“极大极小”(maximin)规则; 就是说,它告诉你要极大化你的极小的可能值。
在吸烟决策中,不吸烟的行为有最高的安全水平,就是说2(见图15)。如果你求稳,便将选择戒烟。
如果恰巧有两个行为的安全水平有同样高的值,你大概会注意哪一个有最高的次低值。
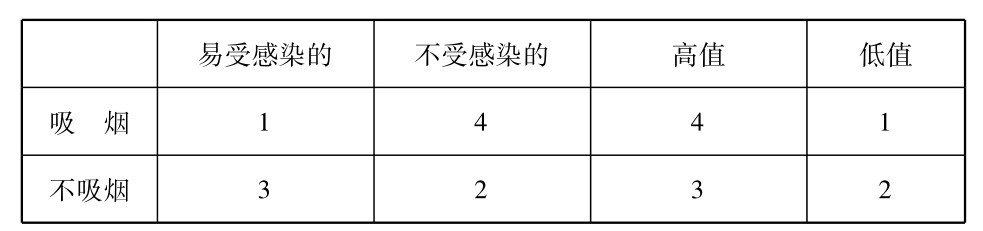
图15 指出高值和低值的吸烟母式
图15再次展现图14的吸烟母式,最右边的是两个可能行为中每一个的最高值和最低值。
赌博者的策略注意每个行为的高值并且选择那个有最高的价值[“极大极大”(maximax)]的行为。求稳策略注意每个行为的低值,并且选择那个有最高的低值(“极大极小”)的行为。是否有理由认为在不确定的场合中,这些策略中的一个本质上比另一个“更合理”呢?
哲学家和决策论者中间公认的答案是: “否。”选择最佳行为或满意的行为确实像是“正确的”做法,但如果那两个规则都不适用,那么唯一合理的选择就是不可能的。
花时间去表述赌博和求稳的策略的主要理由,是对于这两种对决策问题的态度要有个清楚明确的理解。如果你想要赌博或者想要求稳,你清楚地知道怎么办。而如果你需要理解他人或甚至自己已经作出的决策,这两个规则的一个也许正确地描述了所采取的行为。即使你不能辩护这个行为,你也许至少能够理解它。
这种不愉快情况的根本理由是容易发现的。我们是在对世界的状态缺乏任何特定的情报,仅仅晓得这些状态是可能的并且不受我们的行为所左右的条件下处理决策问题的。不应当预期在缺乏确定的科学情报条件下永远可能作出“合理的”决策。如果掌握更多的情报,情况就大不相同了。
3.6 有风险的决策或有风险的抽彩给奖法
决策论者谈到风险时,他们想到的是已知的或被控制的风险。在客观概率已知的条件下,风险就是被控制的。所以,有风险的决策被定义为在知道一切可能状态的概率的场合作出的决策。知道客观概率显然是介于确定性和不确定性之间的一类知识。
关于有风险的抽彩给奖法或有风险的决策,正如不确定的决策一样,经典数理统计传统否认得出合适的损失结构或先验概率的可能性。费希尔、内曼和皮尔逊及其追随者不考虑先验概率和得到结果的代价,而唯一地关心样本数据。在并无关于可能状态的先验情报,也没有按照常规通过π(θ)的合适的形式来表达这种情报的愿望的那些场合,单纯依靠样本数据去作出决策,选择最佳的行为,应当采取什么规则呢?
上节所考虑的完全不确定中的决策规则,即使你的价值母式是仅仅按照可能结果的级别来表示的,也能够应用。有风险的决策规则就不是这样。仅当价值的测度达到这个程度,使值差的比率是有意义的,它们才能够应用。这并不奇怪,因为概率可以看作一种测定的知识。如果你把概率和价值结合起来,价值必须在大致相同程度上被测定。如果它们不是这样,这种结合便不是有意义的。
要把概率和价值结合起来,我们需要一个新概念: 期望值(expectedvalue)。(https://www.daowen.com)
3.7 期望值
让我们举一个简单的例子。假定你参加一个狂欢节,看到一种游戏,这个游戏设置由分为四个相等部分的一个平衡轮子组成。三部分是蓝色的,一部分是红色的。要玩这种游戏你得支出一元,然后让轮子旋转起来。如果它停下时指针在红色部分,你赢得五元,如果它停在蓝色部分,你什么也没有得到。你的问题是要决定是否玩这个游戏。你的决策母式如图16所示。
这个母式和我们用过的其他母式之间的区别,在于它包含两个可能状态的概率,如果你要把这个问题当作已知风险的决策问题,这些概率所含有的情报必须包括在问题中。
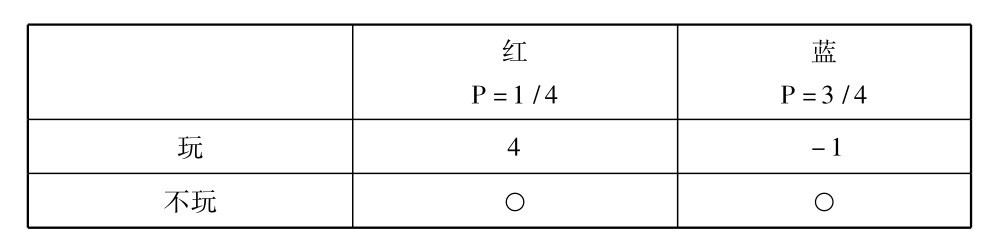
图16 对应于一个简单游戏的母式
图16中所列的价值表示每一可能结果给你带来的纯收益或损失。如果你玩并且赢了,你得五元,但你已付出一元,所以纯收益是四元。如果你输了,你损失一元。如果你不玩,那么不管结果是什么颜色,你既无收益也不会有什么损失。
注意这些价值是严格的金钱价值,如果想把非金钱价值,例如观看轮子旋转并且晓得你可能赢五元所感到的兴奋情绪也包括进去,这是可能的。但这些价值是难以度量的,即使对你自己说也是这样。所以,我们暂以容易度量的金钱价值为限。
在给一个行为的期望值下定义之前,让我们先看看非形式地处理这个问题的几个方式。一个方式是设想玩了大量次数,按平均数计算,你能够期望每输三次便会赢一次,如果事情恰恰像所预期的,你赢一次收益四元,输三次损失三元,在四次中纯收益一元,每次二十五分。
考虑这个情况的另一方式更直接地使用概率,如果你只玩一次,你有四分之一的机会赢得四元和四分之三的机会输掉一元。赢和输是不可兼的析取,你可以把结果相加。四元的四分之一是一元,负一元的四分之三是负零点七五元,两个结果相加便得二十五分。
让我们看看一个行为的期望值的显定义:
一个行为的期望值(EV) 就是它的可能结果的加权和(weightedsum),权即相应状态的概率。
计算加权和的方法是先以其相对应的权来乘每个值,然后把所得的积相加,例如,图(16)的母式所表示的玩这个游戏的期望值是
EV(玩) =(1/4×4元) +(3/4×-1元) =1元-0.75元=25分。
这恰恰是我们上面所计算的。
现在我们就可以明显地陈述已知风险场合中的决策的期望值规则了。
有风险决策的期望值规则:选择那个有最大期望值的行为。
如果恰巧不只一个行为有相同的最大期望值,那么你可以简单地消除所有的其他可能行为,而把余剩的母式当作不确定中的决策场合来处理。已经使用了关于概率的情报来决定期望值,你就没有多余的情报可以用来决定在剩余的几个行为中选择哪一个了。实际上这种情况并不经常发生,所以你不必过分担心这个意外事件。
在狂欢节游戏问题中,这个规则告诉我们去玩这个游戏,因为不玩的期望值是零,而零点二五大于零,就是说,如果你玩,你的期望是一局赚二十五分。如果不玩,你的期望是零。
再举石油钻探例子的简化形式为例,公司的财政情况是这样的:如果有石油,第一年便有纯收益五十万元,如果无石油,便损失钻探费五万元,加上税收、维持费等项一万元,共六万元。如果什么也不干,每年损失一万元。用千美元作为表达价值的单位,所得母式如图17:

图17 简化的石油钻探问题的母式
让我们假定石油公司的地质学家已经决定在和这个地点相类似的地点中发现石油是每五次中出现一次,所以P(石油) =1/5,而P(无石油) =4/5。这两个行为的期望值计算如下:
EV(钻探) =(1/5×$500) +(4/5×-$60)
=$100-$48=$52(千元)
EV(不钻探) =(1/5×-$10) +(4/5×-$10)
=-$2+-$8=-$10(千元)。
第二项计算简直浪费时间,因为两个结果的值都是一样,但可以看出这个公式有效,是令人愉快的。
应用期望值规则便导致钻探的决定。那个行为有大得多的期望值。这样,即使发现石油的概率只是五分之一,如果你得到石油,它的价值这样大,足以抵消这个低的概率。重要的是概率和价值的乘积,而不是两者分开来各自的数量。
有部分知识正如有完全知识一样,也允许考虑行为和状态并不独立的决策问题。在这样的场合,状态的概率将随行为的不同而变化。所以,概率像价值一样,直接同结果相联系,而非同状态相联系。下面是个简单的例子:
假定你参加狂欢节,并且正准备玩图16所表示的游戏。这时你看到对面有另一种相似的游戏。也许这另一种游戏有更高的期望值。你决定去检验它,这样便可扩展你的选择范围。假定你已经决定玩第一种游戏,如果新的游戏有较低期望值的话。这样我们便可以不提及不玩的选择,如图18。
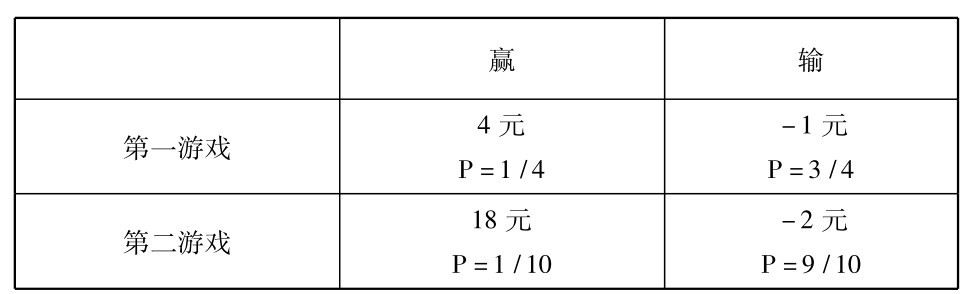
图18 两个不同游戏的选择母式
这种新游戏有十个间隔同样大的数,而非颜色,要化二元去玩,但如果出现十这个数,报酬是二十元。
这样你的决策问题中的可能行为便是: 玩第一游戏还是玩第二游戏。有两个可能状态: “赢”和“输”。每一结果的纯收益和损失是容易计算的。和上文的母式的主要区别,在于概率并不同状态相联,而同结果相联。赢对于每一种游戏有不同的概率,整个母式如图18所示。读者可自己去寻求“正确的”决策。
期望值规则是不是已知风险场合的最好的可能规则呢? 如果有人面对图16的狂欢节游戏时坚持不理会概率,只想求稳——就是说不玩,又怎么样呢? 这个人这样地推理: 在任何一局游戏中,你不可能实际得到期望值二十五分。你要不是赢五元,便是输一元。并没有介于两者之间的结果。而且这个人也许说,损失一元并不是满意的结果,但什么也不损失却是。所以不玩是较好的行为。
对这种担心的通常回答是: 金钱对每个人的真价值并不必然是由实际的金额来表示的。参观狂欢节的一个小孩只有一元可花,把它都花在冒风险的游戏上是愚蠢的。在原则上你也没有什么不同。如果那种游戏的代价是一千元,可能赢得五千元,你也愿意玩吗? 如果代价是十万元或者一千万元呢? 如果你有一百万元,你很可能不愿意为了有增加到四百万元的四分之一机会而冒孤注一掷的风险。你会拿到一百万元就跑。所以一百万元对你的价值比四百万元的仅仅四分之一的机会要大得多。事实上,对大多数人来说,一百万元和四百万元的实在价值并没有多大差别。
因此,如果结果是用你的“实在”价值单位(就是效用,但经典数理统计传统不愿用这个概念)来度量,不一定用金元,那么你就愿意使用期望值规则了,你就不会老是不理会情报而一味求稳了。
有风险的决策通常被看作使用已知概率和结果的价值来决定应当选择哪个行为的过程。如果价值是用金元或银元来表示的,像实际的抽彩给奖法那样,这个决策策略就能很好地解决问题。但对于更注重质的方面的价值,例如吸烟对吸烟者的价值,这个方法的应用就要差一点。在这样的场合,用一种并不必需明显地估定价值的形式提出问题,有时是有帮助的。这时你的价值倒是间接地通过对所要作出选择的仔细考虑而被正视的。
一个简单的作法是设想用一个包含一百颗弹子的坛子来代替每个可能的行为。必定要有各种不同颜色的弹子。这个问题有多少状态你就需要多少种不同的颜色,世界的每个可能状态被分配一个颜色。在行为和状态并不独立的条件下,状态的概率对于每个行为是不同的。你用各种颜色的弹子的相对数来表示状态的概率。一个对于给定行为有二分之一概率的状态便用一百颗弹子中有五十颗带有分配给那个状态的颜色来表示。
一旦所有的坛子都正确地准备好了,你选择一个行为的决定就相当于挑选哪一个坛子。拣出一个坛子后,你必须从那个坛子中随机地选出一颗弹子。被选出的弹子的颜色就告诉你你所得到的是哪个状态,因而是哪个结果。因为你知道每个坛子里的有颜色弹子的数目。拣出一个坛子就表明你是在不明显地对照着各个不同状态的概率来权衡你对那相应的行为的欲望。试设想伸手进去挑出一个弹子是正视你对决策所怀有的真感情的一个生动方式。
现在我将应用这个设计于一个简单的吸烟决策问题。令一颗红色弹子表示活不到六十五岁的状态。一个蓝色弹子表示寿命超过六十五岁的状态。代表选择继续吸烟的那个坛子将有三十八颗红色弹子和六十二颗蓝色弹子。代表戒烟的选择的那个坛子有二十二颗红色的和七十八颗蓝色的。这是因为,根据比较可靠的科学情报,一个吸烟者(男性,二十五岁)活不到六十五岁的概率是百分之三十八。就是说一个吸烟者活到超过六十五岁的概率必定是百分之六十二。假定一个人在二十五岁时戒烟,他的预期寿命将和一个从未吸烟的人大致相同,根据这个假定,如果一个人戒烟,他活不到六十五岁的概率是百分之二十二,因此活到超过六十五岁的相应概率便是百分之七十八。你必须随机地从这两个坛子中的一个选出一颗弹子。选出的是颗红色弹子便意味着: 你将活不到六十五岁。你将选择哪一个坛子呢?
这样提出问题的方式使你正视你的价值,因为你得要自问: 继续吸烟便面对着那个“吸烟”坛子里添加的十六颗红色弹子,值得吗?如果你吸烟,只有你自己才能回答那个问题。
3.8 单纯依赖样本数据的决策规则
经典数理统计传统既不承认效用论,也批评主观概率。因此这个传统把不知道客观概率(因为没有样本数据)的决策问题叫做完全不确定中的决策问题,以别于已知道客观概率的,即有风险的决策问题。对于已知风险的场合,它提出期望值规则作为合理决策的策略。对于完全不确定的场合,首先要问: 是否有最佳行为? 如果有,便采取最佳行为规则(Ba),如果没有,便要再问: 是否有满意的行为?如果有,便采取满意行为规则(Sa)。如果没有,便或者采取赌博者规则,或者采取求稳规则,这往往取决于决策者本人的性格和态度。这各种不同的决策策略,归根结底是单纯由价值母式决定的。如果承认先验概率在决策中的作用,便不致主张决策的完全不确定性,也不会纯凭价值母式来决定一切了。
3.9 对两种决策场合的统一说明
贝叶斯决策论的新形式既承认主观概率,也承认客观概率,并且为我们主观的先验概率的选择提供合理的标准,这就有别于贝叶斯决策论的较流行的、较贫乏的形式: 贝叶斯私人主义。这种形式既否认客观概率也否认选择我们的先验概率的合理标准。
贝叶斯决策论应付包含风险和不确定性的情况,应付我们必须在两个或更多行为方案之间作出选择,然而又不能够有信心地预测采取任一特殊方案的结果的情况。在这样的情况中,不同方案之间的选择能够用不同的抽彩给奖法之间的选择作为模型。在描述这样的抽彩给奖法时我们可以同时使用,也可以不同时使用主观概率和客观概率。
一个给定个人所怀有的主观概率是指刻画这个人自己的选择行为,包括打赌行为的特征的一个参数。例如,我给一个给定钱币的下一次投掷将正面朝上分配二分之一的主观概率,这一个陈述蕴含着我对于它是正面或者反面朝上,同等地愿意打赌。这样,这个陈述关于这个钱币本身的行为什么也不说; 它所谈的仅仅是关于我自己的态度,我自己的行为。
与此相对照,一个客观概率是刻画一个给定物理系统的统计行为的特征的一个物理参数。这样,“一个给定钱币将以客观概率二分之一正面朝上”这个陈述便蕴涵着: 在一个很长序列的投掷中,这个钱币将以靠近二分之一的频率正面朝上。在承认有客观概率的哲学家中间,有些人实际上把客观概率等同于被观察的长流频率(long-run frequencies),其他的人则把它们解释作有关物理系统以特定频率产生给定结果的物理倾向。
下面我们用一些跟上文稍为不同的符号来表示贝叶斯决策论的若干基本概念。
(1)L=(A1│e1; A2│e2; ……; -n│en)
表示一个抽彩给奖法在事件(或状态)e1发生时得奖金A1; 在事件e2发生时得奖金A2; 等等。事件e1,e2……叫做制约事件。假定这些事件构成一个相斥而又穷举的析取。
在事件e1……en有确定的客观概率,而这些客观概率又被决策者知道有以下的值
(2)P(e1) =P1,……,P(en) =Pn,
的特殊场合,也可用下式来表示L,
(3)L=(A1,P1,……,An,Pn)。
当然我们必须有
(4)Pi≥0(i=1,……,n)并且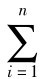 Pn=1。
Pn=1。
一个已知客观概率的抽彩给奖法叫做有风险的抽彩给奖法,而客观概率部分地或全部地未知的抽彩给奖法叫做不确定的抽彩给奖法。
贝叶斯决策论建议把合理行为定义为满足某些使人非相信不可的合理性要求(这些要求被称为贝叶斯合理性公理)的行为。根据这些公理,它证明
期望效用极大化(EUM)定理:一个其行为满足贝叶斯合理性公理的决策者要在不同的抽彩给奖法之间进行选择,便好像力图把他的期望效用极大化。
期望效用被定义为下面的量:
(5)δU(L)=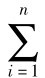 πiU(Ai),
πiU(Ai),
这里U表示决策者的效用函数,δU表示他的期望效用,而π1,……, πn则表示他给制约事件e1,……,en所分配的主观概率。这些主观概率必须满足和(4)相类似的条件。
在L是一个有风险的抽彩给奖法的特殊场合,决策者必须使
(6)πi=Pi(i=1,……,n)
就是说,他必须使他的主观概率πi和事件ei的已知客观概率Pi相等。
我们也可以用以下形式来陈述EUM定理:
(7)U(L) =δU(L),对一切抽彩给奖法L成立。
换句话说,一个合理决策者将使任何抽彩给奖法对他的效用等同于他对这个抽彩给奖法的期望效用。
方程式(7)可以说表达这个事实: 决策者的效用函数U具有期望效用属性。
这样看来,贝叶斯决策论把有风险的抽彩给奖法看作不确定的抽彩给奖法的特殊场合,从而对两种不同情况中的决策作出统一的说明。它的期望效用极大化定理提供在一切不确定情况中作出合理决策的规则。
关于贝叶斯决策论的进一步研究当然要读许多其他的专著。
[1] 林德莱: 《决策》,伦敦1971年版,第50页。
