逆 推 理
逆推理的方向或证据关系同省略式演绎推理相反: 在省略推理中,结论由前提和另外一些命题的合取逻辑地得出,这里所说的另外一些命题被推理者接受为真,但在前提中并未明显地提出。在逆推理中,逻辑推理的方向刚好相反。前提由结论相对于推理者知识中的某些命题逻辑地得出来,也就是说,证据可由假说相对于背景知识逻辑地得出来。这里所指的是证据关系的方向,就是说证据和假说的关系同前提到结论的推断关系相反; 结论并不由前提得出。至于推理者心里先有假说,然后用证据来检验这个假说,还是先有证据,然后寻找能说明它们的假说,那是无关紧要的。这两个推理过程在时间次序上有别,在逻辑方向上则相同,都是逆推理,又称为导致最好说明的推理。
定义9: 逆推理就是这样的推理: 它的前提可由结论,相对于被一定推理者所掌握但在推理中省略掉的背景知识,在推理中逻辑地得出。
这种推理的心理过程严格地说并不是由证据到假说,而是由证据加上这个假说可以给证据提供说明的认识,过渡到对假说的置信。推理的图式可以表示如下:
1. 观察到某一不寻常的或值得注意的事实F。
2. 如果假说H是真的,那么这个事实就会是当然的(会被最好地说明)。
所以 H是可信的(或值得研究的)。
这种推理在日常生活和科学研究中都应用得很频繁。无论假说是由观察到的事实所首先提示出来的,还是它仅仅被这些事实所检验或支持,像科学实验中典型的假说确认过程那样,都是采取这种形式。
例如,我在书房里坐着专心看书,不留心外面发生的事情。过一会儿我停止看书,走到窗前,看到天空多云,车道和人行道都是湿的,但没有下雨。这些观察使我作出结论: 刚才我看书时一定下过雨。在这个推理中,“车道和人行道都是湿的”这个陈述是前提,“刚才下过雨”这个陈述是结论。很显然由这个前提引出的结论并不是由它逻辑地得出的,因为即使并不曾下过雨,车道和人行道也可以是湿的,因为可能洒水车冲洗过街道。但反过来,结论的真就蕴涵前提的真,因为如果刚下过雨(结论),路面便是湿的(前提)。
这个推理中结论和前提之间的推断关系是相对于推理者知道其真的另一陈述而存在的,这个陈述就是: “如果下过雨,那么车道和行人道是湿的。”我们由电灯突然熄灭推论保险丝烧掉,由信封被拆开推论信已被人看过,都是同一类型的推理。当物理学家假定光是一种横波,这是由光的反射、折射,衍射和干涉偏振的事实推论出来的。所有这些事实都可由光的波动说相对于波动定律得出来。这样,由光的反射、折射、干涉、衍射和偏振推论光是一种横波的科学家们是由推断推出理由,因而求助于逆推理。同样,当道尔顿根据组成化合物的元素重量的恒定比例和倍数比例正式提出他的物体原子结构的观念时,他是采取逆推理的; 因为定比定律和倍比定律可由物体原子结构观念的假定必然地得出,而由前者则不—定得出后者。气体分子运动论,电离解理论和许多其他的物理理论都是以逆推理为基础的。
上文已经指出,在主观地不充分置信的推理中,根据以充分置信接受了的前提,我们以小于充分置信的程度d接受其结论。这个推理相对于已经掌握的知识是结论性的,当且仅当这个置信度d并不超过结论相对于前提和我们其余的知识的概率。因此这种推理相对于知识总汇的结论性条件可以用以下不等式来表示:
(1)d≤PK(H/E)
上式中d表示我们接受结论的置信度,E表示前提,而K表示推理者的知识总汇。
按照贝叶斯定理的简单形式,把推理者的知识总汇加以考虑,在知识总汇K的背景下,结论H相对于E的概率便可用下面的公式来表示:
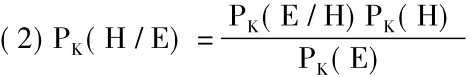
但因为逆推理的前提是由结论和知识总汇K逻辑地得出的,因而
(3)PK(E/H) =1
因为任何推断相对于其理由的概率等于 1,即 H 的似然度(Likelyhood)等于1。
根据(2)和(3),我们便得到我们接受结论的置信度所不能超过的概率PK(H/E):
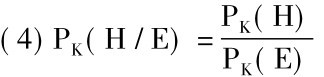
这是在似然度等于1的条件下贝叶斯定理的形式。因而逆推理的归纳强度便是:
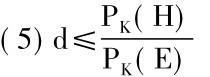
PK(H)是相对于推理者的初始知识总汇的H的概率。新的经验证据即前提E还没有加进去,因而称为H的先验概率或初始概率。另一方面,PK(H/E)是在K的背景下H相对于前提E的概率,即表明推理者不仅知道K而且知道E时对H的置信度,因而称为后验概率。
PK(E)是相对于推理者初始知识总汇的经验证据E的概率,这个概率越高,那么仅仅根据初始知识而并不考虑到H便期望它是真的置信度便越大,这便称为E的先验概率。(https://www.daowen.com)
使用这些名词,用不等式(5)所表示的逆推理的归纳强度便是:在逆推理中,以置信度d来接受的结论是根据充分置信地接受了的前提相对于知识总汇k而接受的,这种推理的归纳强度的高低决定于H的初始概率和E的先验概率的比率。
公式(5)仅当PK(E)≠0时才有意义。这个公式又表明: 如果PK(H) =0,即如果H被初始知识总汇K所排除,那么
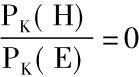
因而 d≤0
这就是说,对结论的置信度不超过零。如果假说H被初始知识总汇所排除,逆推理所作出结论的归纳强度便极低,不能导致H的接受。
公式(5)同时又表明,如果PK(E) =1,即如果逆推理的前提由初始知识总汇得出,那么
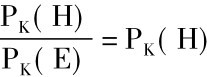
也就是说,这个推理的结论可被接受的归纳强度等于假说H的初始概率。换句话说,从初始知识总汇得出的这些经验证据,并不增加假说的初始概率。
但是,如果 PK(H)≠0
PK(E)≠1
即如果假说H并不被初始知识总汇所排除,而经验证据并不由初始知识总汇得出,那么
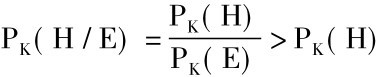
就是说,假说H的后验概率高于它的先验概率。这就表明: 结论并不同初始知识总汇相矛盾,而前提又对初始知识总汇有所增添的逆推理,使我们有理由以比先前所具有的更大的置信度来接受这个假说。因此,对于其真理性我们还未充分置信的某些假说,最适宜于通过逆推理来增加我们对它们所持的置信度。正如公式
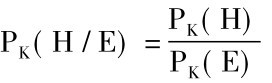
所表明的,PK(E)越低,即证据相对于初始知识总汇的概率越低,假说H相对于其先验概率PK(H)的后验概率PK(H│E)便越高。因此,如果要力图使一个假说可以置信,我们有可能从它和初始知识总汇推演出只根据初始知识总汇概率很低的某些推断; 如果这些推断被证实是真的,我们就可以通过逆推理,根据这些被证实的推断,以比原来大得多的置信度来接受这个假说。
天文学的定律就可以看作随着它们的预测(即由它们得出的推断)被经验所确认而提高了概率的假说。例如对日蚀的预测越准确,它的先验概率就越低; 如果从地面上特定的位置进行观察,所预测的日蚀开始时刻以秒来计算,那就比以小时计算准确得多。如果根据天文学定律作出的以秒计算的始蚀时刻被证实是真的,这就比对同一事实以小时计算的预测被证实,能使这个定律的概率提高得更多。天文学预测是极准确的,因而它们的先验概率是极低的,但所有这些预测都得到证实,这就大大地提高了天文学定律正确性的概率。
定量陈述比定性陈述更准确。例如: “气体的压力随体积的减小而增加”是一个定性陈述,“气体的压力与其体积成反比”是一个定量陈述; 后者比前者更为准确,因而定量陈述比定性陈述的先验概率要低。因此,对于其定理能作出定量预测的那些学科,只要所作出的定量预测能够得到证实,这些学科的定理就具有较高的概率。对于其定理只能作出定性预测的那些学科,即使预测得到证实,其定理的概率仍比前一类定理为低。
很显然,从一个假说H导出的预测的数量越大,并且后来都被证实,这个假说的概率就越高。当一个预测E1被证实时,假说H的概率由下面的公式所表示:
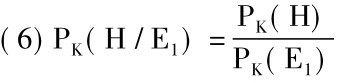
而当它的两个预测E1和E2被证实时,这个假说的概率则由下面的公式所表示:
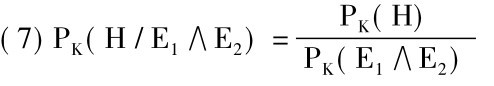
因为我们有
(8)PK(E1∧E2) =PK(E2/E1)PK(E1)
又因为PK(E2/E1)≤1,根据0≤P(A/B)≤1(一个陈述的条件概率从零到1),所以
PK(E1∧E2)≤PK(E1)
仅当E2由E1&K得出,PK(E2/E1) =1才成立。即如果预测E2没有任何新的内容,PK(E2/E1) =1。但如果这种情况被排除,即如果假定PK(E2/E1)≠1,那么我们有
(9)PK(E1∧E2) <PK(E1)
于是根据(6)和(7)得
(10)PK(H/E1∧E2) >PK(H/E1)
这就表明如果我们证实了一个由假说导出的、本质上为新的预测(这就是说该预测并不是根据初始知识总汇K由先前的预测导出的),那么该假说的概率就增加了。新预测E2相对于初始知识总汇和先前预测的概率越小[即它的先验概率PK(E1∧E2)越小],假说的后验概率就增加得越多。
很显然,逆推理本身并不是可靠的,所以,它可能由真前提导致假的结论。然而,既然它在合适条件下使结论(假说)的概率增加,并且在日常实践和科学研究中常常作为一种主观上不充分置信的推理来运用,因而它是一种有用的和有价值的归纳推理。
