第三节 估 计
3.1 小引
关于统计假说的辩护问题,经典数理统计发展了两种不同但相关的方法,也就是两种统计推理。一种方法是根据一个总体的样本的知识,单纯地去估计所关心的属性在那个总体中的百分比,或者说,单纯地估计一个变项的值; 另一种方法是使用关于样本所获得的知识去检验关于那个总体的统计假说。这两种方法在科学中都有广泛用途。
使用一个样本去估计一个总体中的百分比的实验情况在下图4中加以图解:
令字母A代表所关心的属性,例如吸烟者或共和党人。A在总体中的百分比是未知的,是我们所要估计的。这样,从总体中进行任何随机抽样,都有将选出具有属性A的一个个体的一个未知概率P(A)。同样地,就其大小为n的样本来说,便有A在样本中的可能频率的一个未知的抽样分布。样本经过检查,我们就知道了A在样本中的实际的相对频率f(A)。这个事实,加上关于样本是得自一个随机抽样过程的这个知识,便为估计A在总体中的百分比提供了证据。
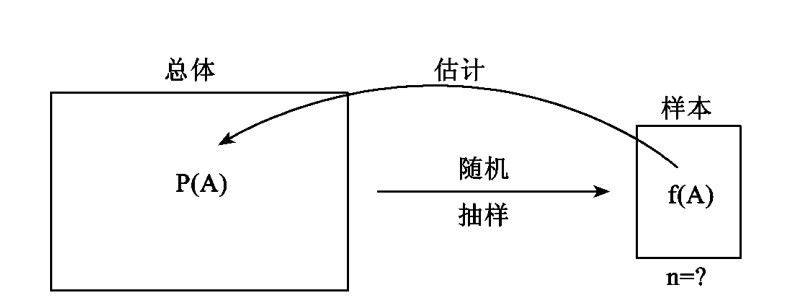
图4 用样本频率f(A)去估计总体比率P(A)
估计是一个归纳过程。因此它的结论即估计的辩护,能够用一个归纳推理的形式来表示。关于这种推理的形式我们需要有更多了解。下面以一个民意测验为例来讨论这种归纳推理。
3.2 简单统计假说的辩护
1981年10月美国纽约时报举行了关于环境保护问题的一次民意测验,并且详细报道了测验结果。其中对于这个问题: 他们是否“希望维持现有的环境保护法,即使对经济增长有损害?”被询问的一千四百七十九位美国成年人中,百分之六十七回答说“是的。”但是,统计假说是关于在总体中的百分比的陈述。关于在超过十八岁的美国成年人总体中会作出相同答案者的百分比,我们能够作出什么结论呢?
“总体中的百分比也是百分之六十七”这个结论是很诱人的。但是,一般地说,一个随机样本中的频率同总体中的百分比恰恰相当的概率是很小的。因而总体中的百分比同样本中的频率恰恰相当的概率也是很小的。假定你试图根据那些被抽样者的百分之六十七希望维持现有的环境保护法这个观察事实,主张这个对于所有美国人的百分之六十七也是真的,则即使你的前提是真的,你的结论真的概率也是很小的。这样,你的推理就不是好的归纳推理。一个好的归纳推理,按照经典数理统计的传统,具有由真前提产生真结论的高概率。因此这个结论是得不到辩护的。
虽然一个随机样本恰恰同总体相当的概率是低的,样本频率同总体的百分比靠近的概率却可以是很高的。在由百分之五十是妇女的总体中取出的五百人的样本中,有百分之九十五的概率保证这个样本将包括百分之四十六至百分之五十四之间的妇女。粗略地说,反过来也是真的。如果由一个五百名美国人的随机样本中得出百分之五十是妇女,那么,妇女在总体中的真比率将包括在百分之四十六至百分之五十四的区间内,其概率是零点九五。
纽约时报的调查报告最后指出: “在理论上能够说根据整个样本所得到结果同访问所有的美国成年人会得到的结果的差别不超过百分之三,这是有百分之九十五的把握的。”这就是说,在所有美国人中的百分比和一千四百七十九人的整个样本中的频率之差在百分之三以内,这有零点九五的概率。因此我们能够构造下面这个好的归纳推理:
一千四百七十九人的随机样本被要求回答关于环境保护的政策问题。
其中百分之六十七说他们希望维持现有的环境法规。
因此(归纳地)可以说希望维持现有环境法规的美国人在百分之六十四和百分之七十之间。
如果这个推理的前提是真的,那么结论也真的概率是零点九五。
这个推理的一般形式可揭示于下:
由总体P随机地选出一个大小为n的样本。S中A的频率是f(A)。
所以(归纳地)A在P中的百分比是f(A) ±ME。
字母ME代表误差范围。误差范围的大小决定于样本的大小。
由上述讨论得到的一个重要的一般教训就是: 决不可能使用一个样本的数据来辩护单单一个简单统计假说。能够得到辩护的顶多只是统计假说的析取,这些假说之间的差别仅仅在于它们给总体的属性所赋予的百分比。这个析取是由所观察样本频率f(A)周围的一个区间来代表的。
由于这个缘故,常常把总体百分比的估计叫做区间估计(interval estimation)。通常把这个区间叫做置信区间(confidence interval)。同归纳推理相联系的概率,上例中的零点九五,则被称为置信水平(confidence level),这些都是经典数理统计所用的术语。
在对抽样分布的研究中,我们知道: 随着样本变大,离开期望频率两个标准差以内的样本频率的范围就会变小。因为这个缘故,随着样本变大,误差范围就变小。准确的计算并不是很困难的,但我们这里无需加以探讨。我们只要对于几个典型的样本量所具有误差边际的大小有一个大致的观念,就足够了。
附表1列出若干样本量的置信区间和误差边际。这些数字假定了样本中被观察到的频率是零点五。显然大多数的所观察频率和这个数有距离。但除非所观察频率相当接近于零或者一,比方说在零点一以下或者零点九以上,所指出的误差边际将是足够准确的。
表1 对于各种不同的样本量中所观察到的样本频率零点五的近似百分之九十五的置信区间
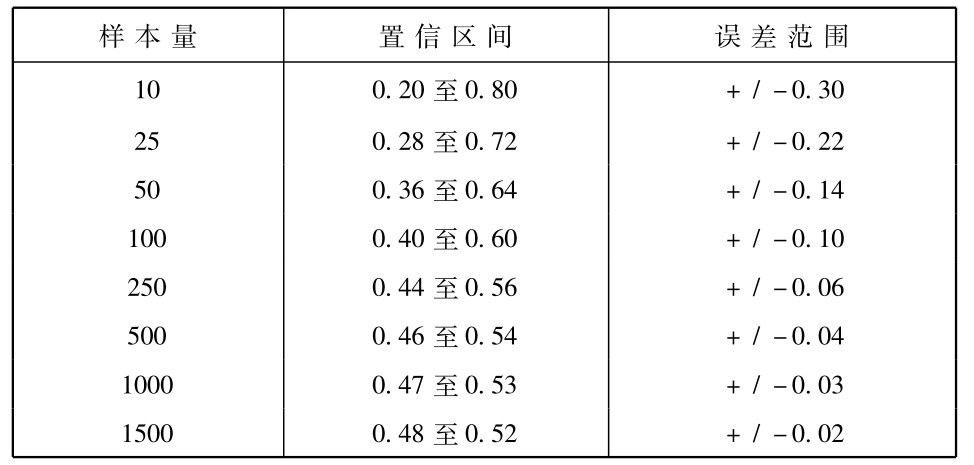
你也许不能够把整个表背熟,但至少在脑子里你应当有下列粗略的根据经验和实际得来的规则。对一百的样本来说,误差范围大致是百分数十点; 对五百的样本来说大致是五点; 超过一千的样本误差边际小于三点。只要有了这三个参考数值,你在对根据随机样本的统计结论进行评估时就能够充分应付了。
要说明对样本大小和误差边际之间关系的理解是很有用的,可再看看纽约时报民意测验的资料,其中一项显示出百分之五十四的黑人应答者说他们希望环境保护继续改进,不管经济上有多大损失。人们也许被诱使作出结论: 过半数黑人支持这个立场。要是容许百分之三的误差范围,便支持这个结论。但误差边际并不只是百分之三。那个误差范围假定了超过一千人的样本。报告说被访问黑人的数量反映出黑人在整个总体中的百分比。这样,在一个约一千五百人的样本中,黑人不能够超过一千,因为那就是认为黑人构成整个总体的大约三分之二了,你知道这是不可能的。那么黑人的样本究竟多大呢?
要进一步研究,你需要知道报告中并不包含的一个事实。就是说,你需要知道黑人在整个总体中的百分比。你并不需要准确地知道百分比多大。一个粗略的估计就足够了。这时你应该想一想你是否对美国人口有任何知识,可据以作出关于黑人所占百分比的有根据的猜测。你需要知道的事实是: 美国黑人约占整个美国人口的百分之十五。这样,一个有百分之十五黑人的、略小于一千五百人的样本会包括大约二百二十五个黑人。附表Ⅰ上所列的最接近的样本量是二百五十。这是一个得出百分之六误差边际的整数。但是,即使你仅仅使用上面提及的粗略的经验估算法,误差范围应在百分之五和百分之十之间(如果黑人样本是五百人,它便是百分之五,如果是一百人,它便是百分之十)。这样,即使我们把误差边际算作只是百分之五,得到辩护的结论将是: 一切成年黑人中会作出相同答复者的百分比在百分之四十九和百分之五十九之间。而我们知道实际区间比这个还要宽。所以,过半数黑人、即超过百分之五十的黑人支持这个立场的结论并没有真的得到辩护。被辩护的结论允许真的百分比有小于百分之五十的可能性。
作为上文的摘要,让我们使图4完善,以便作出关于借助区间估计以辩护统计假说的一幅完全的图画。图5表示纽约时报民意测验仅仅考虑所有那些说他们愿意保持现有的环境保护法规的美国人的百分比。总体由超过十八岁的美国成年人组成。这个图解所显示的是随机地由总体选出的一千四百七十九人的样本。
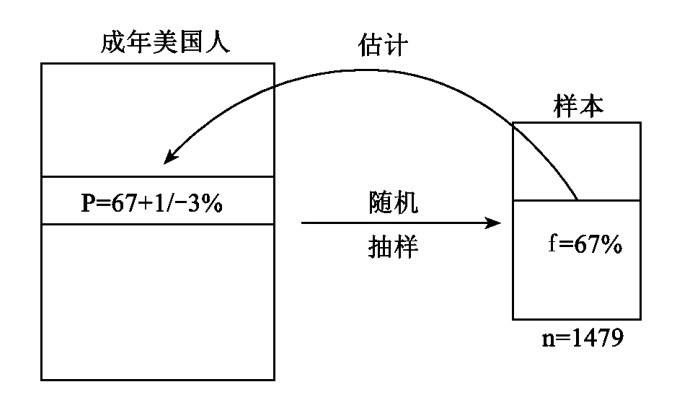
图5 估计那些说他们愿意维持现有环境保护法规的美国人的百分比
所指属性在样本中的频率f(A)是百分之六十七。区间估计所得出的有好理由的结论是: 整个总体中会作出相同答复的人将在百分之六十四和百分之七十之间。
3.3 相关
一个相关的描述就是两个简单统计假说的合取。这样,辩护一个相关假说就只是辩护两个有关的统计假说的问题。使用区间估计方法,这就要有两个区间估计。
回头看看纽约时报的报告。关于说他们希望维持现有的环境保护法规的不同年龄的应答者的数字,报告指出,那些十八岁至二十九岁的人有百分之八十作肯定的答复,同六十五岁和超过六十五岁者的仅仅百分之五十三恰好成为对照。因此这个样本显示出年龄变项和对这个问题的答复之间是相关的。在样本中,是十八岁到二十九岁同对这个问题的肯定回答正相关。这是否使我们有理由作出整个总体中也存在着同样的相关的结论呢?
由于事实上年龄变项有四个值,不是仅仅两个值,这个例子有点复杂。最容易的处理方法是一次仅仅考虑两个值。纽约时报记者就仅仅考虑最低的和最高的年龄值。这就是说: 我们只考虑总体的一部分,即那些或在三十岁以下或在六十四岁以上的人。
为了构造适当的区间估计,我们需要大致知道样本每一部分中的被调查人数。不幸,甚至最好的调查报告也常常忽略这些关键性的材料,这份报告也只告诉我们每个年龄组的被调查人数反映出这一组在整个总体中的实际比例。但因为很少人知道这些比例,所以这个材料是没有什么价值的。我们只能够作出有根据的猜测。如果这个样本是等分为四个年龄组的,那么每一组就约有三百五十人。一个谨慎的假定是每一组至少有二百五十人。说“谨慎”,因为这也许小于实际的人数。因此,如果使用这个数,我们将得到比我们实在有理由得到的较宽的区间。因此我们就使这一点成为不大可能: 在相关的结论不合理时我们仍将作出这样的判断。当然这就使另一方面的错误的可能性稍许大些: 在有好理由作出相关的结论时,我们将判断没有相关。一般地说,谨慎一点,在一律不主张并无好理由的相关这个方向上犯错误较好。
回头看表1,我们见到二百五十人的样本的误差边际是百分之六,于是我们作出结论: 所有十八岁至二十九岁者会作肯定答复的百分比所在的区间并不大于百分之七十四和百分之八十六(80+ / -6%)之间的区间。同样地,在六十五岁和以上的那些人中间,肯定答复的比率所在的区间并不比百分之四十七和百分之五十九(53+/-6%)之间的区间更大。既然即使这些估计过大的区间也并不重叠,我们就有理由作出结论: 较年青那一组的肯定答复比率真的是较高。所以,是在十八岁至二十九岁这一组内和对问题作出肯定答复之间有正相关这个结论就好像是有好理由的。
与此相对比,试考虑黑人和白人对问题的答复。在样本中,黑人的肯定答复比率是百分之五十四,而白人的比率是百分之六十一。这些数据使我们有理由主张在总体中种族差别和问题的肯定答复有相关吗?
我们再次必须构造两个适当的区间。这就要求对于每个组内应答者的人数作出判断。知道了样本的调整是要反映黑人和白人在总体中的相对人数,我们在上文已推算约有二百五十个黑人。这就剩下了大约一千二百五十个白人。因此黑人的区间约在百分之四十八和百分之六十(54+/-6%)之间,而白人的区间则大致在百分之五十八和百分之六十四(61+/ -3%)之间。这两个区间相重叠。因此,按照我们的有最好理由的结论,这两个百分比不能够和总体中的百分比相同,样本中所观察到的差别也许仅仅由于抽样中的随机波动。这就是说,有相关的主张是没有好理由的。
因此,我们辩护相关假说的归纳方法可以概述如下:
为每个部分的简单因果假说构造区间估计。如果得到的区间并不重叠,相关假说便是有理由的。如果这些区间相重叠,这个假说便是没有理由的。
我们在第一节中根据两个相关百分比之间的差额来定义相关强度。现在我们已经懂得我们关于这些百分比的结论必定是不同百分比的区间,那么关于相关强度我们又能合理地作出什么结论呢?
你也许已经猜到,答案就是: 我们关于任何相关强度的估计也必定是值的区间,在大多数用途上,简单地取两个部分统计假说的两个最靠近一端之间的差额和两个最远离一端之间的差额就够了。这就得出那构成我们关于相关强度的估计的一个区间。
例如,我们把年龄和希望维持现有环境保护法规之间的相关强度估计为在零点一五(0.74-0.59)和零点三九(0.86-0.47)之间。同样地,种族和对现有环境保护法规的态度之间的相关强度将被估计为在负零点零二(0.58-0.60)和零点一六(0.64-0.48)之间。后一估计包括零强度的可能性这个事实就表明为什么那个相应的相关假说不是有理由的。
区间代表不确定性,而大多数人都不喜欢不确定性。他们希望有确定的答案——一个单一的数。但学会科学推理的一部分就是学会正确地判断不确定性的价值和聪明地对待不确定性。严格地说,断定一个单一的、准确的数值的任何假说都是不能够得到辩护的。能够被辩护的顶多就是那个值周围的一个小区间,那也许就需要一个很大的样本。
图6是对于年龄和对现有环境保护法规的态度之间的相关的民意测验的图解。你应当很好地注意这个图解的各个不同成分,以便能够对于提出相关问题的其他研究构造一个类似的图解。
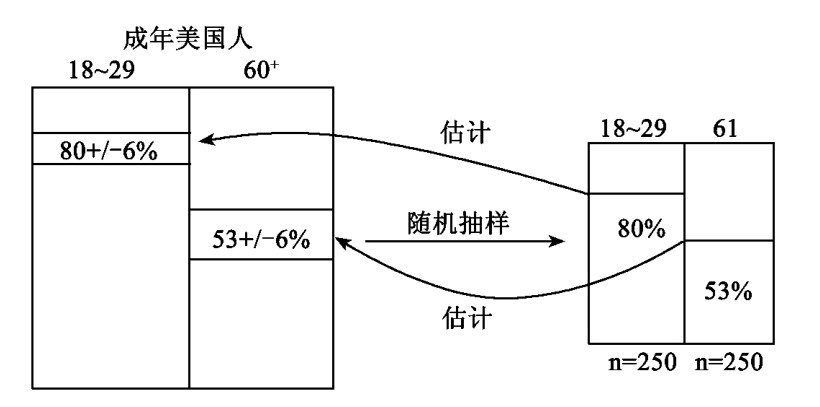
图6 估计在美国成年人中间年龄和表示维持现有环境保护法规的愿望之间的相关
3.4 和抽样调查有关的问题
区间估计是一个归纳方法,任何时候只要发现一个随机地选出的样本显示出有已知相对频率的某一属性,就可以使用这个方法。抽样调查属于这个范畴,但由于它是用来评估在大的和性质十分不同的总体中人们的态度的,便产生出特殊的问题。这些特殊问题可大致分为两类: 关于数据可靠性的问题和关于选择过程的随机性问题。
在意见调查(或民意测验)中获得的资料也许不可靠的一个理由,就是人们并不总是作出诚实的答复。1986年8月6日《人民日报》称:“最近,辽宁省统计局对三十个县、区的一万二千三百六十六名成年人进行了选择配偶条件和理想结婚年龄意愿的调查……在‘你认为当前男女找对象的主要条件是什么’的问题中,有百分之七十八点六的人回答是对方的人品,他们认为道德品质最为重要; 有百分之七点二的人认为,是对方的文化程度; 有百分之六点二的人认为,是对方的家庭条件; 有百分之四点一的人认为,是对方的工作条件; 有百分之三点九的人着重对方的外貌形象。前两项合计占百分之八十五点八。”所以《人民日报》记者作出结论: “普遍认为择偶的主要条件是人品。”对于择偶的主要条件问题,由于社会上好像有一个“正确意愿”的“框框”(即《人民日报》记者所谈的“前两项”: 人品和文化程度),并非所有的调查对象都愿意讲真话,特别是对“官方”的调查员讲真话。所以后三项(即家庭条件、工作条件和外貌)所占百分比是否真的那么低,是可以怀疑的。至于记者所作的结论,顶多是就样本来说的(百分之八十五点八决不等于“普遍”),我们是否能够根据样本中的这个百分比,作出结论: 在整个辽宁省成年人或甚至整个中国成年人的总体中,百分比也同样是百分之八十五点八呢?根据你关于抽样分布的知识,你知道一个随机样本同总体恰恰相符的概率是很低的,所以,这样的结论不能够是有理由的。但更重要的是下面要谈到的选择过程的随机性问题,这涉及样本本身是否有“偏倚”(bias)的问题。
关于资料的不可靠性还有一点要注意: 即使人们并不有意说谎,他们也是常常会弄错的。例如,试考虑通过调查吸烟者来研究吸烟与健康的关系问题。通常是询问人们的吸烟习惯(何时开始吸烟? 一天抽多少支烟? 是否吸入肺部?)和他们的一般健康状况。在这样的场合你也许得不到很准确的答案。人们会忘记他们是何时开始吸烟的,有些健康不佳的人也许把吸烟看作方便的替罪羊而把他们吸烟的量估计得太多,而健康良好的人担心吸烟可能的害处,也许过低估计吸烟的量,甚至自己不愿意承认每天不只抽一包。关于健康状况也是一样。人们往往忘记过去的病史,如此等等。由于这一类的问题,所以大多数有关健康问题的严肃研究,不能限于调查访问,而需要作出实际的医学检查。
所以,在读关于民意测验或抽样调查的报告时,你必须对于数据也许不可靠或者令人产生错误想法的各种可能方式,有所警惕。特别要当心: 人们对一位访问者所说的和他们真正相信的或者真实的情况也许大有出入。
其次要考虑抽样的非随机性问题。
在抽样调查,特别是民意测验中,所关心的总体(目标总体target population)是所有中国人的一个很大的子群——例如,所有达到选举年龄的成年人,所有已登记的选民,所有妇女,所有达到结婚年龄的成年人。要建立一个使目标总体内的每个人都有相等的机会被选出的抽样系统是很费力的,也很费钱。实际上被抽样的总体,即那些确实有相等机会被选出的人们,已经只是目标总体的一个子群了。因此这样的危险永远存在: 这个实际上被抽样的子群对于目标总体的代表性是不够的。如果它是不够代表性的,那么,不管多么大的样本,结论对于原来所关心的总体将是不正确的。
这种错误的一个典型例子是1936年美国《读者文摘》杂志所举办的一次民意测验。一千万张样品选举票被邮寄给由全国各地电话簿内选出的人们。寄回的选举票超过两百万张,显示出共和党候选人兰登比较民主党候选人罗斯福占明显的优势。而事实上,在选举中罗斯福获百分之六十的选票。试想想问题出在哪里呢?
问题在于1936年美国处于经济大萧条当中。在电话簿上有名字的人们往往在经济上属于上层; 而收入较低的人,特别是失业者,往往家里不设电话,但这些人都强烈地支持罗斯福。所以,由于电话业务、经济地位和党派偏爱之间的强烈相关,民意测验显示出兰登的多数票,而事实上选民的大多数是偏爱罗斯福的。主要由于这次测验的惨败,1937年《读者文摘》宣告停刊。
这个故事的教训是: 在读任何调查报告时,你应当特别注意所用的抽样方法,如果你幸而对这方面的情况有所知晓的话。自己试想想被抽样的总体也许和目标总体不相同的各种可能方式,然后考虑是否这些差别也许对于所得结论是相干的。如果关于抽样方法人家一点也不告诉你,对于调查结果你应当保留一定程度的怀疑态度。
在进行调查的各种不同方法中间,邮寄问题表是特别不好的方法,因为抽样过程的随机性受到寄回比率——寄回问题表的百分比的强烈影响。通常这个比率相当低,这简单地因为大多数人都不愿意花工夫填好问题表并且寄回。须知《读者文摘》民意测验中的寄回比率只有百分之二十。而且,那些愿意花时间的人往往对于所讨论问题有强烈的意见。特别是如果已知道抽样调查的主办者是支持某一特殊看法的,赞成这个看法的人们一般地作出回答的可能性便较大。所以,当你读到通过送出问题表进行调查所得的结果时,永远要注意寄回比率。如果寄回比率低,要想想在愿意寄回问题表同以这一种或那一种方式回答问题之间是否可能有强烈相关。如果有,由寄回的问题表中算出的百分比必定错误地表现了整个总体。即使你想不出在回答和回答动机之间的任何明显相关,也很可能是有些相关的,你仍旧应当保留怀疑态度。
