概率的逻辑解释
概率的逻辑解释的意图是要说明“概率”的归纳用途。因此它认为概率演算是用陈述而不是用属性的措词来表述的。按照逻辑的解释,条件概率表达有关陈述之间的逻辑关系(尽管这些逻辑关系和我们在演绎逻辑研究中所遇见的关系是不同的)。当然在一种意义上,显然在“概率”的归纳用途中,P(q/p)必定表达陈述p和陈述q之间的逻辑关系,就是说,它给那个以p为前提和以q为结论的推理的归纳强度评定等级。
但断言条件概率表达有关陈述之间的逻辑关系还有另外的意思。这意思就是:为概率赋值的陈述,即P(q/p)=a,是分析的,它们的真或假并不决定于事实。根据逻辑的解释,P(q/p)的值单独决定于“概率”的意义以及陈述“p”和“q”的意义,而同事实无关。因此,对于决定概率值,任何经验研究都是不相干的,正如对于决定p∨~p这个陈述的真或假,任何经验研究都是不相干的一样。换一个方式来说,根据逻辑的解释,为概率赋值的陈述,P(q/p) =a,并不提出任何关于事实的主张。相反,根据相对频率的解释,这样一个陈述的确对于相对频率或相对频率的极限作出事实的断定。因此根据相对频率的解释,经验研究对于概率值的决定是相干的。
有些人坚持认为逻辑解释而非频率解释对于说明概率的归纳用途是必要的。他们这样推理: 归纳概率P(q/p)为p给予q的证据支持决定等级。但如果像P(q/p) =a这样的概率陈述被解释为对事实有所主张,那么必定要根据现有证据e对它们作出归纳评价。要这样做,我们必须使用归纳概率[P(q/p) =a/e]。但给这个归纳概率赋值也是作出事实的断定,而要评价这个关于事实的断定,我们又必须知道另一个归纳概率,如此等等以至无穷。为了要知道一个归纳概率的值,我们必须已经知道无限多的其他归纳概率的值。如果这是事实,归纳逻辑就永远不能够起步。这样,逻辑解释的提倡者争辩说,选择任何其他的解释来说明概率的归纳用途都要导致无穷回归(infinite regression)。
根据逻辑解释,概率赋值是分析的。但不应当因此认为,逻辑解释便不能够说明经验资料。P(q/p) =a这个陈述是分析的,但陈述p和陈述q都可以作出事实的断定(的确它们可以是关于相对频率的陈述; 这样,逻辑解释允许我们运用归纳概率来评价一个关于相对频率的陈述给予另一陈述的证据支持,或者反过来。换一个方式来说,根据逻辑解释,一个陈述p的认识概率决定于我们的知识储备恰恰有什么经验资料,这样,虽然Pa(q/p) =a是分析的,Pe(q) =a却不是分析的。
我们将用卡尔纳普所提出的解释的简化形式作为概率的逻辑解释的一个例子。设想只有两个名字a和b和两个(逻辑地独立的)属性F和G的一种简单语言。这种语言的简单陈述是Fa,Fb,Ga,Gb。复杂陈述借助逻辑联结词由简单陈述构造出来,正如复杂属性那样。一个状态描述是含有每个原子陈述或其否定作为合取肢,却不同时含有两者的合取陈述。我们的语言的状态描述如下:
1. F(a)∧G(a)∧F(b)∧G(b)
2. F(a)∧G(a)∧F(b)∧~G(b)
3.F(a)∧G(a)∧~F(b)∧G(b)
4.F(a)∧G(a)∧~F(b)∧~G(b)
5.F(a)∧~G(a)∧F(b)∧G(b)
6.F(a)∧~G(a)∧F(b)∧~G(b)
7.F(a)∧~G(a)∧~F(b)∧G(b)
8.F(a)∧~G(a)∧~F(b)∧~G(b)
9. ~F(a)∧G(a)∧F(b)∧G(b)
10. ~F(a)∧G(a)∧F(b)∧~G(b)
11. ~F(a)∧G(a)∧~F(b)∧G(b)
12. ~F(a)∧G(a)∧~F(b)∧~G(b)
13. ~F(a)∧~G(a)∧F(b)∧G(b)
14. ~F(a)∧~G(a)∧F(b)∧~G(b)
15. ~F(a)∧~G(a)∧~F(b)∧G(b)(https://www.daowen.com)
16. ~F(a)∧~G(a)∧~F(b)∧~G(b)
关于a和b所具有的属性,每一状态描述都描绘了一个可能的状况。当且仅当以一个给定的状态描述为它的唯一前提而以一个陈述为它的结论的那个推理是演绎地正确的,我们才说这个陈述在这个状态描述中是有效的。例如,F(a)在状态描述1到8中有效,一个重言式例如F(a)∨~F(a)在一切状态描述中都有效。一个矛盾陈述例如F(a)∧~F(a)在无一状态描述中有效。现在我们便能够给出概率演算的逻辑解释如下:

乍一看来,这个解释好像是很合理的,它给予每一状态描述同等的先验概率。但是,卡尔纳普已证明这个解释将给归纳逻辑带来灾难性的后果。如果我们接受这个解释,那么将永远是P(a)(q) =P(a) (q/p)。结果,q的认识概率将永远等同于它的先验概率,而不受知识储备e的影响。概率演算的任何解释要是导致知识储备对于一个陈述的认识概率不相干这个结果,就不能够说明“概率”的归纳用途。我们必须另外寻找一个能够说明这种归纳用途的逻辑解释。
设想那些是合取属性的复杂属性,它含有每一简单属性或其否定,但不同时含有两者作为其合取肢。这些叫做Q属性。该语言中的Q属性有:
Q1: F∧G
Q2: ~F∧G
Q3: F∧~G
Q4: ~F∧~G
注意在出现表中每一Q属性只在恰恰一个情况中出现,并且在每一情况中恰恰有一个Q属性:
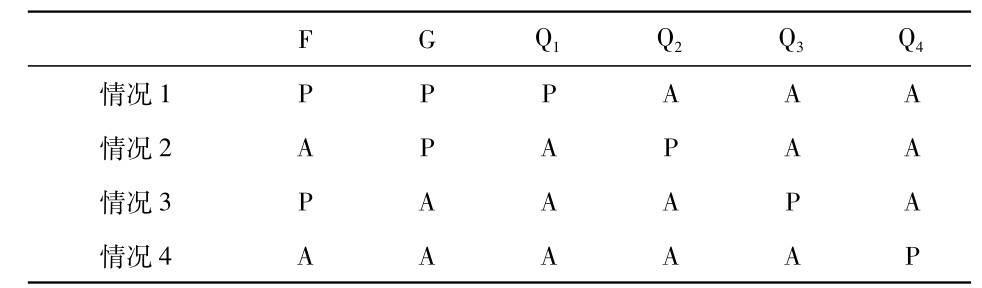
(上表的“P”表示出现,“A”表示不出现。)
状态描述能够很容易地按照Q属性的措词来重新表述。例如,状态描述1变成Q1(a)∧Q2(b),状态描述2变成Q1(a)∧Q3(b),状态描述3变成Q1(a)∧Q2(b)等等。
我们将把指出多少个体具有每—Q属性的陈述叫做结构描述。例如一个结构描述如下: 一个个体具有Q1和一个个体具有Q4,但没有任何个体具有Q2或Q3。和一个给定的结构描述相对应的可能有不止一个状态描述。例如状态描述4和13便相应于这个给定的结构描述(因为状态描述4可重新表述为Q1(a)∧Q4(b),而13可重新表述为Q4(a)∧Q1(b)。对应于同一结构描述的一些状态描述被称为互相同构的。另一方面,有些结构描述可能只有一个相应的状态描述。例如,只有一个状态描述相应于下述结构描述: 两个个体都具有Q1,而没有任何个体具有Q2或Q3或Q4。下页第一表列出十个结构描述以及和它们相对应的状态描述。
现在我们不对状态描述配给同等的先验概率,却为结构描述配给同等的先验概率。在我们的图表中,我们给每一结构描述分配十分之一的值。当只有一个状态描述相应于一个结构描述时,我们便把配给那个结构描述的概率值分配给它。这样,状态描述1,11,6和16便每个都有十分之一的先验概率。当多于一个状态描述同一个给定的结构描述对应时,我们便把配给那个结构描述的概率等分地配给那些相应的状态描述。因此我们图表中所有其他的状态描述都有二十分之一的先验概率,最后我们将使一个陈述的先验概率等于那个陈述在其中有效的一切状态描述的先验概率的总和。按照这样的方向我们提出概率演算在给定语言L中的解释如下:
第1表
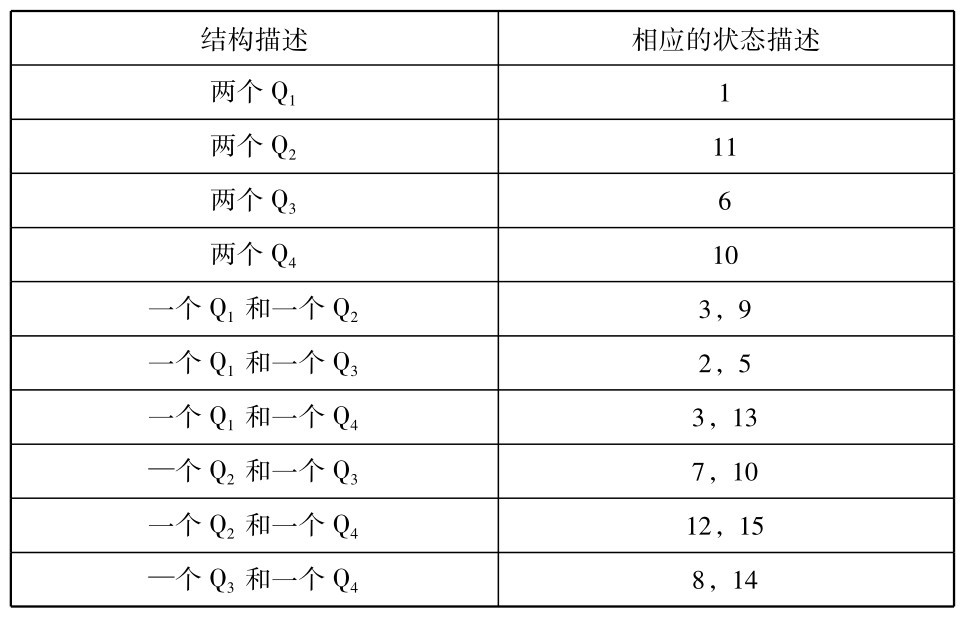
令S是L中的一个状态描述,令a是L中的结构描述数,b是和S同构的状态描述数,那么
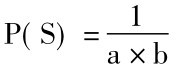
对于L中的任何陈述p,Pa(p) =p为在其中有效的一切状态描述的概率之和。
[如果p是自相矛盾的,因而并不在任何状态描述中有效,那么Pa(p) =0。]
条件概率将按照通常的方式下定义。概率演算的这个解释避免了前面那个解释的困难。它允许我们的知识汇集以合理的方式对认识概率发生影响。但是,它还远不是完美的解释,其理由我们这里不能详谈。总之,寻求合理的逻辑解释的努力已取得一些成就,请进一步研究卡尔纳普和欣迪卡的有关著作。
