2.3.2 矩阵
矩阵是MATLAB的基本处理对象,也是MATLAB的重要特征.在MATLAB中,二维数组称为矩阵.
一、矩阵的创建方法
1.直接输入法
MATLAB中创建矩阵最简单的方法是使用矩阵创建符号[].在方括号内输入多个元素可以创建矩阵的一个行,并用逗号或空格把每个元素间隔开,不同行的元素之间用分号分隔.例如:输入命令
![]()

这样,MATLAB工作空间中就建立了一个矩阵A,以后就可以使用矩阵A了.
也可以用回车符代替分号,按下列方式输入:

方括号只能创建二维矩阵,包括0×0、1×1和1×n矩阵.
2.构造特殊矩阵
MATLAB提供了多个创建不同矩阵的函数,见表2-4.利用这些函数可以创建各种特殊矩阵.
表2-4 特殊矩阵构造函数
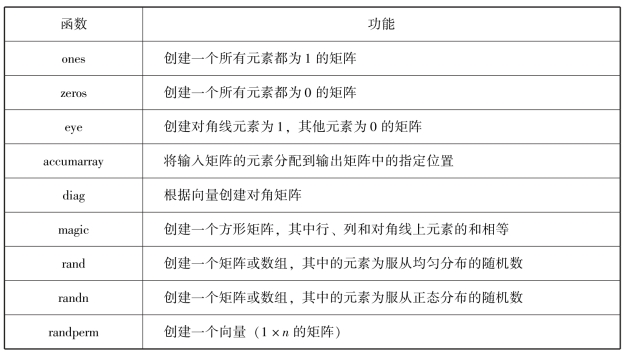
表2-4中的大部分函数返回double型的矩阵.但是,可以用ones、zeros和eye函数很容易生成任何数值类型的基本数组.
要做到这一点,需要将MATLAB数据类型名称作为最后一个变量,例如:

又如,下面的代码创建一个5×5魔方矩阵.
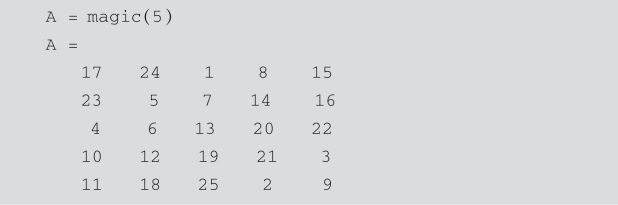
注意,每一行、每一列和每个人对角线上的数值加起来都等于65.
下面的代码创建元素为服从均匀分布的随机数的矩阵或数组,将每个元素乘以20.
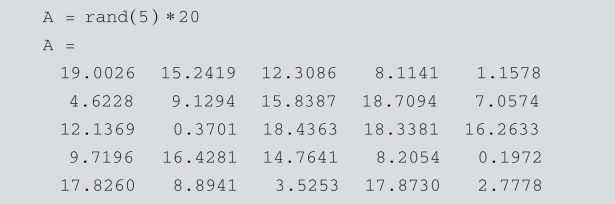
下面的代码根据向量创建一个对角矩阵.可以将向量元素放在矩阵的主对角线上,或者放在主对角线的上方或下方,如下所示,其中-1表示将向量元素放在主对角线下方.


3.建立大矩阵
大矩阵可由方括号中的小矩阵建立起来.例如:

其中,eye(3)返回3×3单位矩阵;ones(3)返回3×3全1矩阵.
二、矩阵的拆分
1.矩阵元素
MATLAB允许用户对一个矩阵的单个元素进行赋值和操作.例如,如果想将矩阵A的第3行第2列的元素赋为200,则可以通过下面语句来完成:
![]()
这时将只改变该元素的值,而不影响其他元素的值.如果给出的行下标或列下标大于原来矩阵的行数或列数,则MATLAB将自动扩展原来的矩阵,并将扩展后未赋值的矩阵元素置为0.例如:

在MATLAB中,也可以采用矩阵元素的序号来引用矩阵元素.矩阵元素的序号就是相应元素在内存中的排列顺序.矩阵元素按列编号,先第一列,再第二列,依此类推.例如:

2.矩阵拆分
(1)利用冒号表达式获得子矩阵
①A(:,j)表示取A矩阵的第j列全部元素;A(i,:)表示A矩阵第i行的全部元素;A(i,j)表示取A矩阵第i行、第j列的元素.
②A(i:i+m,:)表示取A矩阵第i~i+m行的全部元素;A(:,k:k+m)表示取A矩阵第k~k+m列的全部元素;A(i:i+m,k:k+m)表示取A矩阵第i~i+m行内,并在第k~k+m列中的所有元素.例如:

又如:

③A(:)将矩阵A每一列元素堆叠起来,成为一个列向量,而这也是MATLAB变量的内部储存方式.例如:

在这里,A(:)产生一个6×1的矩阵,等价于reshape(A,6,1).
利用MATLAB的冒号运算,可以很容易地从给出的矩阵中获得子矩阵,这样处理的速度比利用循环语句来赋值的方式快得多,所以,在实际编程时,应该尽量采用这种赋值方法.
(2)利用空矩阵删除矩阵的元素(https://www.daowen.com)
在MATLAB中,定义[]为空矩阵.给变量X赋空矩阵的语句为X=[].注意,X=[]与clearX不同,clear是将X从工作空间中删除,而空矩阵则存在于工作空间,只是维数为0.
将某些元素从矩阵中删除,采用将其置为空矩阵的方法就是一种有效的方法.例如:

其中,第二条命令将删除A的第2列和第4列元素.输出为:

三、矩阵的运算
1.基本算术运算
MATLAB的基本算术运算有+(加)、-(减)、∗(乘)、/(右除)、\(左除)、^(乘方).这些算术运算的运算规则不难理解,但必须注意,运算是在矩阵意义下进行的,单个数据的算术运算中是一种特例.
(1)矩阵加减运算
假定有两个矩阵A和B,则可以由A+B和A-B实现矩阵的加减运算.运算规则是:若A和B矩阵的维数相同,则可以执行矩阵的加减运算,A和B矩阵的相应元素相加减.如果A和B的维数不相同,则MATLAB将给出错误信息,提示用户两个矩阵的维数不匹配.
一个标量也可以和其他不同维数的矩阵进行加减运算.例如:

(2)矩阵乘法
假定有两个矩阵A和B,若A为m×n矩阵,B为n×p矩阵,则C=A+B为m×p矩阵,其各个元素为:
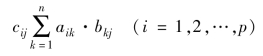
例如:

矩阵A和B进行乘法运算,要求A的列数与B的行数相等,此时则称A、B矩阵是可乘的,或称A和B两矩阵维数相容.如果两者的维数不相容,则将给出错误信息,提示用户两个矩阵是不可乘的.
在MATLAB中,还可以进行矩阵和标量相乘,标量可以是乘数,也可以是被乘数.矩阵和标量相乘是矩阵中的每个元素与此标量相乘.
(3)矩阵除法
在MATLAB中,有两种矩阵除法运算:\和/,分别表示左除和右除.如果A矩阵是非奇异方阵,则A\B和A/B运算可以实现.A\B等效于A的逆左乘B矩阵,也就是inv(A)∗B,而B/A等效于A的矩阵逆右乘B矩阵,也就是B∗inv(A).
对于含有标量的运算,两种除法运算的结果相同,如3/4和4\3有相同的值,都等于0.75.又如,设a=[10.5,25],则a/5=5\a=[2.1000 5.000].对于矩阵来说,左除和右除表示两种不同的除数矩阵和被除数矩阵的关系.对于矩阵运算,一般A\B≠A/B.例如:

(4)矩阵的乘方
一个矩阵的乘方运算可以表示成A^x,要求A为方阵,x为标量.例如:

显然,A^2即A∗A.
矩阵的开方运算是相当困难的,但有了计算机后,这种运算就不再显得那么麻烦了,用户可以利用计算机方便地求出一个矩阵的方根.例如:


2.点运算
在MATLAB中,有一种特殊的运算,因为其运算符是在有关算术运算符前面加点,所以叫点运算.点运算符有.∗、./、.\和.^.两矩阵进行点运算是指它们的对应元素进行相关运算,要求两矩阵的维数相同.例如:

A.∗B表示A和B单个元素之间对应相乘.显然与A∗B的结果不同.
如果A、B两矩阵具有相同的维数,则A./B表示A矩阵除以B矩阵的对应元素,B./A等价于A./B.例如:

显然x./y和y.\x值相等.这与前面介绍的矩阵的左除、右除是不一样的.
若两个矩阵的维数一致,则A.^B表示两矩阵对应元素进行乘方运算,例如:


指数可以是标量.例如:

底也可以是标量.例如:

点运算是MATLAB很有特色的一个运算符,在实际应用中起着很重要的作用,也是许多初学者容易弄混的一个问题.下面再举一个例子进行说明.
当x=0.1、0.4、0.7、1时,分别求y=sin xcos x的值.命令应当写成:

其中求y的表达式中必须是点乘运算.如果x是一个标量,则用乘法运算就可以了.
